棋盘覆盖 题解

Posted 2022-08-30 donkey2603089141

给出一张n* n(n< =100)的国际象棋棋盘，其中被删除了一些点，问可以使用多少1* 2的多米诺骨牌进行掩盖。

可转换为二分图最大匹配。

```cpp
代码

#include<bits/stdc++.h>
using namespace std;
const int maxn=10010;
int cx[4]=1,0,0,-1;
int cy[4]=0,1,-1,0;
int n,m,x,y,a[110][110];
bool used[maxn];
int match[maxn];
int tot;
int ver[maxn*2],Next[maxn*2],head[maxn];
void add(int x,int y)
    ver[++tot]=y,Next[tot]=head[x],head[x]=tot;

int getnum(int x,int y)
    return (x-1)*n+y;

bool dfs(int x)
    for(int i=head[x];i;i=Next[i])
        int y=ver[i];
        if(!used[y])
            used[y]=1;
            if(!match[y]||dfs(match[y]))
                match[y]=x;
                return true;
            
        
    
    return false;

int main()
    scanf("%d %d",&n,&m);
    for(int i=1;i<=m;++i)
        scanf("%d %d",&x,&y);
        a[x][y]=1;
    
    for(int i=1;i<=n;++i)
        for(int j=1;j<=n;++j)
            if(!a[i][j])
                for(int p=0;p<4;++p)
                    int nowx=i+cx[p];
                    int nowy=j+cy[p];
                    if(nowx>=1&&nowx<=n&&nowy>=1&&nowy<=n&&!a[nowx][nowy]&&(nowx+nowy)%2)
                        add(getnum(i,j),getnum(nowx,nowy));
                    
                
            
          
        
    
    int ans=0;
    for(int i=1;i<=getnum(n,n);++i)
        memset(used,0,sizeof(used));
        if(dfs(i)) ++ans;
    
    printf("%d",ans);
    return 0;

T4 数星星

题意

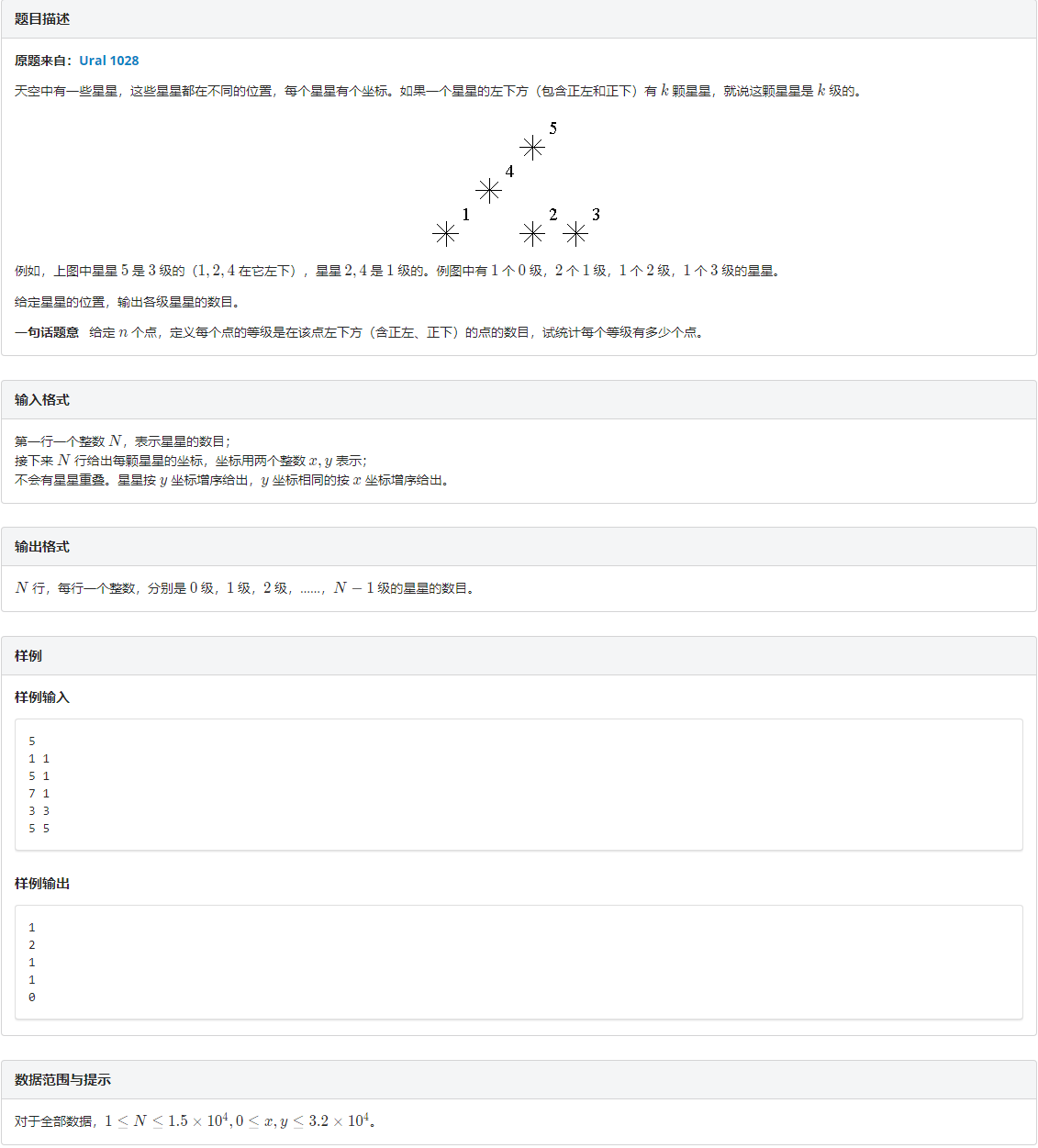
一道水题，由于x坐标递增y坐标也递增于是前缀和统计即可，用树状数组实现。

#include<bits/stdc++.h>
using namespace std;
const int maxn=15010;
const int maxx=32010;
inline long long read()
    long long x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9')
        if(ch=='-')
            f=-1;
        ch=getchar();
    
    while(ch>='0'&&ch<='9')
        x=(x<<1)+(x<<3)+(ch^48);
        ch=getchar();
    
    return x*f;

long long n,c[maxx],ans[maxn];
long long lowbit(long long x)
    return x&(-x);

void add(long long x)
    for(x;x<=maxx;x+=lowbit(x)) c[x]+=1;

long long ask(long long x)
    long long tmp=0;
    for(;x;x-=lowbit(x)) tmp+=c[x];
    return tmp;

int main()
    n=read();
    for(long long i=1;i<=n;++i)
        long long x,y;
        x=read();y=read();
        long long s=ask(x+1);
        add(x+1);
        ans[s]++;
    
    for(long long i=0;i<n;++i)
        printf("%lld\n",ans[i]);
    
    
    return 0;

/*
5 
1 1
5 1
7 1
3 3
5 5
*/

```