暑假考试题4：星际旅行（欧拉路）

Posted 2022-08-26 mowanying

 

 

题目：

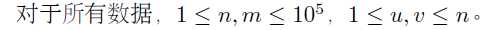
分析：

题目大意：从任意点出发，任意点结束，在经过所有边的情况下选择两条边只经过一次，其它都经过两次。

先不考虑自环：这道题看起来很像欧拉路，但欧拉路是每条边只经过一次，那么我们考虑：把边数翻倍，选择两条边删去，使得剩下的是一个欧拉路。

边数翻倍后，每一个点的度数都是偶数

欧拉路的判定：只有两个点是奇数点，其它都是偶数点（奇偶指度数）证明

找不同的两条边删去，再考虑自环的因素，就应该分类讨论：

1.删两条边：通过画图推出，删的两条边一定是连在同一个点上，因为只有这样才会出现两个奇数点。

2.删一个自环和一条边：删掉一个自环后，那个点的度数仍旧是偶数，随便删掉一条边，会产生两个奇数点，所以显然每个自环都可以和另外所以的边搭配。

3.删两个自环：删掉后，剩下所有点仍是偶数点，所以是一条欧拉回路，也满足条件（两个自环走一次，其它走两次）。

但是可能出现有不连通的情况，所以应该用并查集特判一下，不满足则输出0。

注意：像这种数据：一个连通块+一个孤点，也是满足的。所以说并查集不能对点做，而应该对边做，换句话说，这里的连通指的是边的连通！！！

那么怎么对边做并查集呢？

还是先输入点，然后把点并在一起。在判断的时候，只对有连边的点判断是否在一个并查集了，对于没有边的点不用管。

复杂度：O(N)

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define N 100005
int fa[N],a[N],b[N];
ll ans=0,self=0,du[N];
int find(int x)

    if(fa[x]==x) return x;
    return fa[x]=find(fa[x]);

int main()

    freopen("tour.in","r",stdin);
    freopen("tour.out","w",stdout);
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) fa[i]=i;
    for(int i=1;i<=m;i++)
        scanf("%d%d",&a[i],&b[i]);
        if(a[i]==b[i]) self++;
        else
            int f1=find(a[i]),f2=find(b[i]);
            fa[f1]=f2;
            du[a[i]]++; du[b[i]]++;
        
    
    int f=find(a[1]);
    for(int i=2;i<=m;i++) if(find(a[i])!=f)  printf("0\\n"); return 0; //对边做并查集 
    for(int i=1;i<=n;i++)
    if(du[i]>1) ans+=du[i]*(du[i]-1)/2;//C(n,2)累加答案 
    if(self&&self!=1) ans+=self*(self-1)/2;//特判一下 以免运行时错误 
    ans+=self*(m-self);
    printf("%lld\\n",ans);
    return 0;

/*
5 4 
1 2
1 3
1 4
1 5

10 10
2 4
4 4
4 6 
6 6
6 7
7 5
5 8
8 4
4 9
9 10
*/