百度之星java大数+C++做法Strassen

Posted 2022-08-25 tangent-1231

 

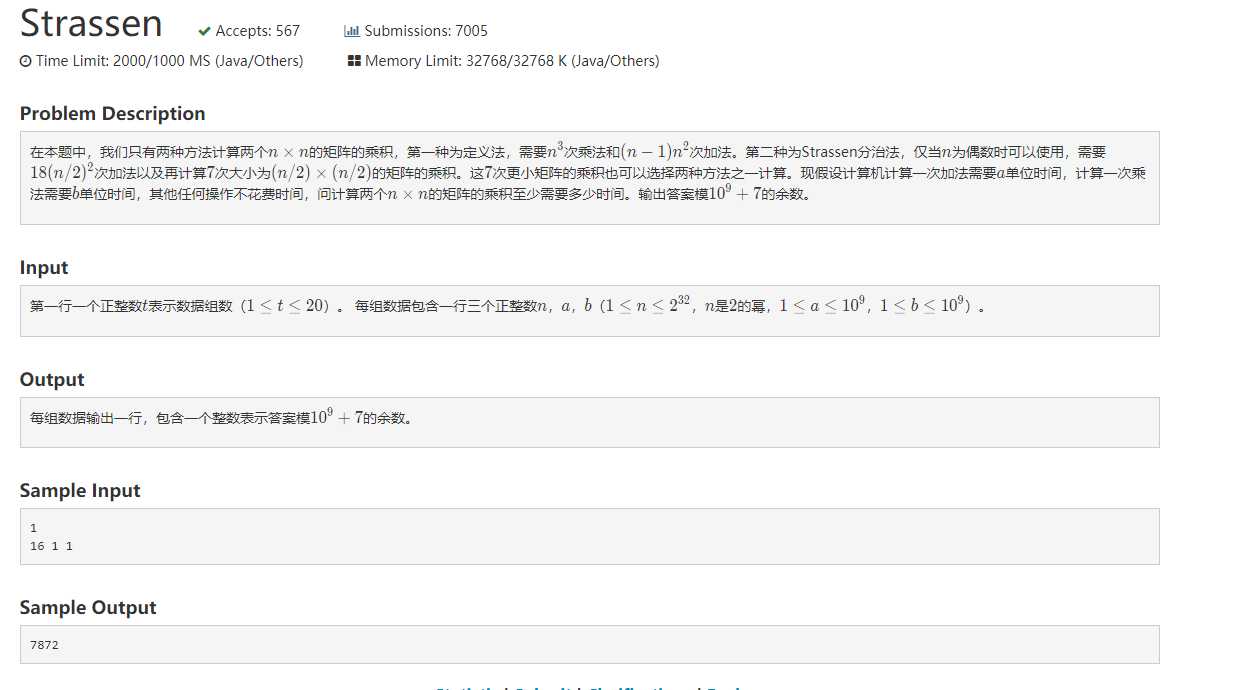
代码：递归搜索一下。java大数做法

import java.util.*;
import java.math.*;
import java.security.MessageDigest;

public class Main 
     static BigInteger s=BigInteger.ONE.add(BigInteger.ONE);
    public static void main(String[] args) 
        Scanner cin=new Scanner(System.in);
        int T;
        T=cin.nextInt();
        while(T-->0)
        
            BigInteger a,b,n;
            
            n=cin.nextBigInteger();
            a=cin.nextBigInteger();
            b=cin.nextBigInteger();
            BigInteger ans=cul(n,a,b).mod(BigInteger.valueOf(1000000007));
            System.out.println(ans);
            
        
    
    public static BigInteger cul(BigInteger n,BigInteger a,BigInteger b)
    
        if(n.equals(BigInteger.ONE))
        
            BigInteger sum1=n.multiply(n).multiply(n).multiply(b).add(n.subtract(BigInteger.ONE).multiply(n).multiply(n).multiply(a));
            return sum1;
        
        return min((n.divide(s)).multiply(n.divide(s)).multiply(BigInteger.valueOf(18)).multiply(a).add(cul(n.divide(s),a,b).multiply(BigInteger.valueOf(7))),n.multiply(n).multiply(n).multiply(b).add(n.subtract(BigInteger.ONE).multiply(n).multiply(n).multiply(a)));
    
    private static BigInteger min(BigInteger add, BigInteger add2) 
        // TODO Auto-generated method stub
        if(add.compareTo(add2)<0)
            return add;
        else return add2;
    

 

C++：

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<queue>
#include<set>
#include<cmath>
#include<string>
#include<map>
#include<vector>
#include<ctime>
#include<stack>
using namespace std;
#define mm(a,b) memset(a,b,sizeof(a))
typedef long long ll;
const long long mod = 1e9 + 7;
const int maxn = 1e5 + 10;
const ll inf = 1e18;
ll a, b;
ll f1(ll n) 
    n %= mod;
    return (n*n%mod*n%mod*b%mod + n * n%mod*(n - 1) % mod*a%mod) % mod;

ll f2(ll n) 
    if (n % 2) return f1(n);
    if (n <= 30 * a / (a + b)) return f1(n);
    return (18 * (n / 2) % mod*(n / 2) % mod*a%mod + 7 * f2(n / 2) % mod) % mod;

int main()

    int t;
    ll n;
    cin >> t;
    while (t--)
    
        scanf("%lld%lld%lld", &n, &a, &b);
        printf("%lld\\n", f2(n));