定心,规范化,白化
Posted redo19990701
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了定心,规范化,白化相关的知识,希望对你有一定的参考价值。
输入定心
定心是通过更改输入\\(\\mathttX\\)的原点移除输入中的偏差,即使得变换后的输入\\(\\mathttZ\\)均值为零
输入的平均值\\(\\bar\\mathttx=\\frac1N\\mathttX^T1\\)
- \\[\\mathtt x=\\beginbmatrix x_0\\ x_1\\ \\vdots\\ x_d\\ \\endbmatrix\\] \\(\\mathtt x\\in R^(d+1)*1\\)
- \\[\\mathttX=\\beginbmatrix\\mathttx_1^T\\\\\\mathttx_2^T\\\\\\vdots\\\\\\mathttx_N^T\\\\\\endbmatrix\\] \\(\\mathtt X\\in R^N*(d+1)\\)
- \\(\\mathtt1=\\beginbmatrix1\\\\1\\\\\\vdots\\\\1\\\\\\endbmatrix\\) \\(\\mathtt 1\\in R^N*1\\)
转换后的输入\\(\\mathttz_n=x_n-\\barx\\)
或者\\(\\mathttZ=X-1\\barx^T\\)
证明变换后输入均值为零
\\(\\mathtt\\barz=\\frac1NZ^T1=\\frac1NX^T1-\\frac1N\\barx1^T1=\\barx-\\frac1N\\barxN=0\\)
输入规范化
定心是通过对输入\\(\\mathttX\\)进行特征缩放,使得变换后的输入\\(\\mathttZ\\)每个特征标准差为1
以下讨论建立在定心的基础上
标准差计算方法\\(\\sigma=\\sqrt\\frac1N\\sum_n=1^N(x_i-\\barx)^2\\),由于已经定心(\\(\\barx=0\\)),所以\\(\\sigma=\\sqrt\\frac1N\\sum_n=1^Nx_i^2\\)
标准差\\(\\sigma_i=\\sqrt\\frac1N\\sum_n=1^Nx_ni^2\\)
变换后\\(\\mathttz_n=\\beginbmatrixx_n1/\\sigma_1\\\\\\vdots\\\\x_nd/\\sigma_d\\\\\\endbmatrix=\\mathttDx_n\\)
- D是对角矩阵,\\(\\mathttD_ii=1/\\sigma_i\\)
或者\\(\\mathttZ=XD\\)
证明变换后标准差为1
\\(\\sigma_i(\\mathttz)=\\sqrt\\frac1N\\sum_n=1^Nz_ni^2=\\sqrt\\frac1N\\sum_n=1^N\\fracx_ni^2\\sigma_i^2=\\sqrt\\frac1\\sigma_i^2*(\\frac1N\\sum_n=1^Nx_ni^2)=1\\)
输入白化
如果输入特征之间相关性较高,那么在做正则化时对不同特征的独立惩罚就很难做到,白化的作用就是减少特征间的相关性,同时使得所有特征具有相同的方差
白化是使得输入每个维度相同重要,降维是衡量输入维度的重要性然后舍弃不重要的维度,所以降维不应该在白化之后
以下讨论建立在定心的基础上
协方差矩阵\\(\\mathttC=\\frac1N\\sum_n=1^Nx_nx_n^T=\\frac1NX^TX\\)
- \\(C_ij=cov(x_i,x_j)\\) 该协方差描述了\\(x_i\\)和\\(x_j\\)的相关性
- \\(cov(x,y)=E(xy)-E(x)E(y)=E(xy)\\)这里已经定心过,所以\\(E(x)=E(y)=0\\)
- \\(\\mathttx_nx_n^T=\\beginbmatrixx_1x_1&x_1x_2&\\cdots&x_2x_d\\\\x_2x_1&x_2x_2&\\cdots&x_2x_d\\\\\\vdots&\\vdots&\\ddots&\\vdots\\\\x_dx_1&x_dx_2&\\cdots&x_dx_d\\\\\\endbmatrix\\) 这下看懂了吧
转换后输入\\(\\mathttz_n=C^-\\frac12x_n\\)(这里矩阵的开方我也不是很懂)
或者\\(\\mathttZ=XC^\\frac12\\)
白化后的输入的协方差矩阵
\\(\\mathtt\\frac1NZ^TZ=C^-\\frac12(\\frac1NX^TX)C^-\\frac12=C^-\\frac12CC^-\\frac12=(C^-\\frac12C^\\frac12)(C^\\frac12C^-\\frac12)=E\\)
最后得到一个单位矩阵,即\\(cov(x_i,x_j)=\\begincases1,i=j\\\\0,i\\neqj\\endcases\\),这说明每个输入特征只与自身相关,与其它特征不相关
图示
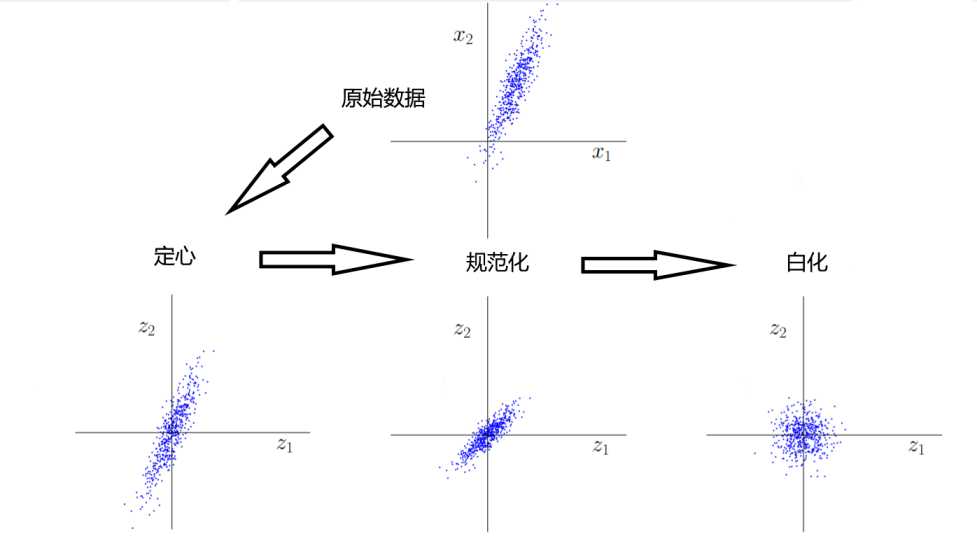
以上是关于定心,规范化,白化的主要内容,如果未能解决你的问题,请参考以下文章