FFT简单总结(持续更新)
Posted evan704
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了FFT简单总结(持续更新)相关的知识,希望对你有一定的参考价值。
FFT简单总结
前言
相信大家都知道大(chou)名(ming)鼎(zhao)鼎(zhu)的FFT(fake_fake_true)(fast_fast_tle),并且都有过被它各种玄学操作虐待的经历(大佬请绕路),那么希望这篇详细的FFT简介能够帮到你。
注:本文中的多项式的次数默认为2的整数次幂,实际中如果不是,需在后面补0。
What it is?
快速傅里叶变换(FFT)是一种能在$O(nlogn)$时间内将一个多项式转换为它的点值表示的算法。、
什么?你不知道点值表示?好吧我也不知道
划重点
设$A(x)$为一个$n-1$次多项式,我们将$n$个不同的$x$带入,得到$n$个$y$,这$n$对$(x,y)$就可以确定1个$n-1$次多项式。并不会证明
引入
FFT一般用来加速多项式乘法,也就是处理一个A(x)*B(x)的乘积C(x)。
考虑暴力算法,即$O(n^2)$枚举每一项并相乘。这样做嘛,太慢了!!!
既然我们刚刚学了点值表示,不妨用点值表示试一试?
一番尝试后我们发现,对于点值表示中的每个$x_i$,都有$C(x_i)=A(x_i)*B(x_i)$,而$A(x_i)$和$B(x_i)$就是点值表示中的$y_i$!如此一来,只要$O(n)$枚举$x_i$就可以算出$C(x)$的点值表示,从而得到答案了!
我们成功的将这个过程提速到了$O(n)$!耶!完结撒花!!!
你以为到此就结束了吗?并没有!
我们仔细一想,发现暴力求解$A(x)$和$B(x)$的点值表示居然要$O(n^2)$!(卒,死因:自闭)
所以,我们还有一个问题:加速求解多项式的点值表示。
FFT:这个我会!!
DFT
诶诶,不是FFT吗??没错,这是FFT的前身。
在讲DFT之前,先讲讲复数。
复数
复数,可以理解为一个点的坐标,分两部分,一个是实部,一个是虚部。$a+bi$中,$a$是实部,$b$是虚部($i$是$\\sqrt-1$)。这里将实部作为横坐标,虚部作为纵坐标。
但与点不同的是,它还是个数,可以代入,可以运算。
这里特别说一点,复数的乘法:
在几何意义上,定义为模长相乘,幅角相加。模长是向量的模长,幅角是从x轴正方向逆时针旋转到与当前向量重合经过的角。
在代数上,
$(a+bi)*(c+di)$
$=ac+bci+adi+bdi^2$
$=ac+bci+adi-bd$
$=(ac-bd)+(bc+ad)i$
正文
FFT(DFT)点值表示中用到的$n$个$x$不是随便找的,而是在单位圆(圆心为原点,半径为1的圆)上$n$等分后的$n$个等分点所表示的虚数。
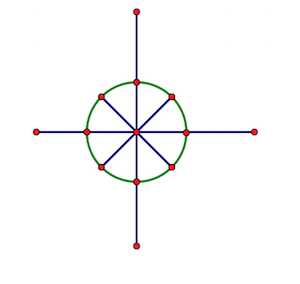
从(1,0)开始,将$n$个点从0编号,设第k号节点代表的虚数为$w^k_n$,即它的实部为$cos \\frackn 2\\pi$,虚部为$sin \\frackn 2\\pi$。根据复数相乘时模长相乘,幅角相加,$w^k_n$的模长为1,幅角为$\\frackn 2\\pi$,所以$w^k_n$为$w^1_n$的$k$次方。我们将这n个特殊的$x$代入,得到了一种特殊的点值表示。
【公式恐惧症患者请速速离开现场】
特殊点性质:
$1. w^dk_dn=w^k_n$
(代表的虚数一样)
$2. w^k+\\fracn2_n=-w^k_n$
(对应点关于原点对称)
不明情况的吃瓜群众:所以为啥要代入特殊点?
当然是因为代入特殊点后的点值表示有特殊性质啦。
将多项式$A(x)$代入特殊点后的点值表示作为多项式$B(x)$的系数,再将每个特殊点取倒数后代入$B(x)$得到的点值表示的每个数除以$n$,得到的是$A(x)$的系数。
证明嘛,本人由于太弱,并不会证,引用一位大佬博客的证明:

至此,我们学会了DFT(啊哈哈哈哈哈哈哈哈哈猖狂地大笑)
不明情况的吃瓜群众:可它还是$O(n^2)$的啊
呃,不然我们要FFT有什么用呢?
FFT
终于,终于到了FFT。FFT其实就是在DFT的基础上加上了一个分治。
我们先将多项式$A(x)=a_0+a_1x+\\cdots+a_n-1x^n-1$拆开变成
$A(x)=(a_0+a_2x^2+\\cdots+a_n-2x^n-2)+(a_1+a_3x^3+\\cdots+a_n-1x^n-1)$
设两个多项式
$A1(x)=a_0+a_2x+\\cdots+a_n-2x^\\fracn2-1$
$A2(x)=a_1+a_3x+\\cdots+a_n-1x^\\fracn2-1$
可得$A(x)=A1(x^2)+xA2(x^2)$
代入一个特殊点$w^k_n (k<\\fracn2)$:
$A(w^k_n)$
$=A1(w^2k_n)+w^k_nA2(w^2k_n)$
$=A1(w^k_\\fracn2)+w^k_nA2(w^k_\\fracn2)$
再考虑$A(k+\\fracn2)$:
$A(w^k+\\fracn2_n)$
$=A1(w^2k+n_n)+w^k+\\fracn2_nA2(w^2k+n_n)$
$=A1(w^k+\\fracn2_\\fracn2)+w^k+\\fracn2_nA2(w^k+\\fracn2_\\fracn2)$
$=A1(-w^k_\\fracn2)-w^k_nA2(-w^k_\\fracn2)$
$=A1(w^k_\\fracn2)-w^k_nA2(w^k_\\fracn2)$
一番魔改之后,我们终于可以分治了,边界为$n=1$,递归求解$A1(x)$和$A2(x)$。
代码部分
递归
//并不是本人的代码,因为递归实现常数过大,一般不会使用,给一份大佬的代码(部分)
//本代码中出现的complex类型是c++STL自带的,不建议使用,最好自己手打
typedef complex<double> cp
cp omega(int n, int k)
return cp(cos(2 * PI * k / n), sin(2 * PI * k / n));
void fft(cp *a, int n, bool inv)
if(n == 1) return;
static cp buf[N];
int m = n / 2;
for(int i = 0; i < m; i++) //将每一项按照奇偶分为两组
buf[i] = a[2 * i];
buf[i + m] = a[2 * i + 1];
for(int i = 0; i < n; i++)
a[i] = buf[i];
fft(a, m, inv); //递归处理两个子问题
fft(a + m, m, inv);
for(int i = 0; i < m; i++) //枚举x,计算A(x)
cp x = omega(n, i);
if(inv) x = conj(x);
//conj是一个自带的求共轭复数的函数,精度较高。当复数模为1时,共轭复数等于倒数
buf[i] = a[i] + x * a[i + m]; //根据之前推出的结论计算
buf[i + m] = a[i] - x * a[i + m];
for(int i = 0; i < n; i++)
a[i] = buf[i];
递推
递推FFT需要经过仔细观察才能发现(反正我没有发现)。
递归FFT中,我们将每一项不断分组递归求解子问题,而递推我们需要预处理出递归最后每个初始位置分治后的位置。(有点绕口)
初始位置:0 1 2 3 4 5 6 7
第一轮后:0 2 4 6|1 3 5 7
第二轮后:0 4|2 6|1 5|3 7
第三轮后:0|4|2|6|1|5|3|7
“|”代表分组界限。
结论:一个位置a上的数,最后所在的位置是“a二进制翻转得到的数”,例如6(011)最后到了3(110),1(001)最后到了4(100)。
所以,递推FFT要我们一个位置a上的数,最后所在的位置是“a二进制翻转得到的数”,例如6(011)最后到了3(110),1(001)最后到了4(100)。先把每个数放到最后的位置上,然后不断向上还原,同时求出点值表示。
//洛谷P3803 会T #include<iostream> #include<cmath> using namespace std; const int N=1e7+5; const double PI=acos(-1.0); int lena,lenb,n=1,lim,r[N]; struct cp//手打加速 double x,y; cp(double _x=0,double _y=0) x=_x;y=_y; cp operator*(cp b) return cp(x*b.x-y*b.y,x*b.y+y*b.x); cp operator+(cp b) return cp(x+b.x,y+b.y); cp operator-(cp b) return cp(x-b.x,y-b.y); a[N],b[N],buf[N]; inline int read()//本题要卡常 int x=0,f=1; char ch=getchar(); while(ch<‘0‘||ch>‘9‘) if(ch==‘-‘)f=-1; ch=getchar(); while(ch>=‘0‘&&ch<=‘9‘) x=x*10+ch-‘0‘; ch=getchar(); return x*f; void FFT(cp *A,int tp) for(int i=0;i<n;i++)if(i<r[i])swap(A[i],A[r[i]]); for(int i=1;i<n;i<<=1) cp W(cos(PI/i),tp*sin(PI/i));//单位根 for(int j=i<<1,k=0;k<n;k+=j) cp w(1,0);//n等分 for(int l=0;l<i;l++,w=w*W)//buf充当一个缓存数组 buf[k+l]=A[k+l]+w*A[k+i+l]; buf[k+i+l]=A[k+l]-w*A[k+i+l]; for(int j=0;j<n;j++)A[j]=buf[j]; int main() scanf("%d%d",&lena,&lenb); while(n<=lena+lenb)n<<=1,lim++; for(int i=0;i<=lena;i++)a[i].x=read(); for(int i=0;i<=lenb;i++)b[i].x=read(); for(int i=0;i<n;i++)r[i]=(r[i>>1]>>1)|((i&1)<<(lim-1));//预处理,r[i]表示初始位置为i的数最后分治到的位置 FFT(a,1);//计算点值表示 FFT(b,1); for(int i=0;i<=n;i++)a[i]=a[i]*b[i]; FFT(a,-1);//计算系数 for(int i=0;i<=lena+lenb;i++)printf("%d ",(int)(a[i].x/n+0.5));
考虑优化buf数组。
我们发现buf数组存在的意义只是为了更新答案并避免更新时的错误而建立的一个缓存数组,所以我们可以将运算内容先记录下来,舍弃buf数组。
这个优化还有个高大上的名字:蝴蝶操作(虽然我并不知道为啥要这么叫)
//洛谷P3803
#include<iostream> #include<cmath> using namespace std; const int N=1e7+5; const double PI=acos(-1.0); int lena,lenb,n=1,lim,r[N]; struct cp double x,y; cp(double _x=0,double _y=0) x=_x;y=_y; cp operator*(cp b) return cp(x*b.x-y*b.y,x*b.y+y*b.x); cp operator+(cp b) return cp(x+b.x,y+b.y); cp operator-(cp b) return cp(x-b.x,y-b.y); a[N],b[N]; inline int read() int x=0,f=1; char ch=getchar(); while(ch<‘0‘||ch>‘9‘) if(ch==‘-‘)f=-1; ch=getchar(); while(ch>=‘0‘&&ch<=‘9‘) x=x*10+ch-‘0‘; ch=getchar(); return x*f; void FFT(cp *A,int tp) for(int i=0;i<n;i++)if(i<r[i])swap(A[i],A[r[i]]); for(int i=1;i<n;i<<=1) cp W(cos(PI/i),tp*sin(PI/i)); for(int j=i<<1,k=0;k<n;k+=j) cp w(1,0); for(int l=0;l<i;l++,w=w*W) cp x=A[k+l],y=w*A[k+i+l];//替代buf A[k+l]=x+y; A[k+i+l]=x-y; int main() lena=read();lenb=read(); while(n<=lena+lenb)n<<=1,lim++; for(int i=0;i<=lena;i++)a[i].x=read(); for(int i=0;i<=lenb;i++)b[i].x=read(); for(int i=0;i<n;i++)r[i]=(r[i>>1]>>1)|((i&1)<<(lim-1)); FFT(a,1); FFT(b,1); for(int i=0;i<=n;i++)a[i]=a[i]*b[i]; FFT(a,-1); for(int i=0;i<=lena+lenb;i++)printf("%d ",(int)(a[i].x/n+0.5));
例题及题解
https://www.luogu.org/problem/P3803 洛谷P3803 https://www.cnblogs.com/Evan704/p/11406308.html
以上是关于FFT简单总结(持续更新)的主要内容,如果未能解决你的问题,请参考以下文章