优化算法1-梯度下降

Posted 2022-08-21 cymx66688

1.1     梯度下降

梯度下降，全称Grandient Descent，简称GD。

梯度下降是一种非常通用的优化算法，能够为大范围的问题找到最优解。梯度下降的中心思想就是迭代地调整参数，从而使成本函数最小化。

首先，初始化一个随机的θ值（可设θ=0），然后逐步改进，每次踏出一步，就尝试降低一点成本函数，直到算法收敛出一个最小值，见下图所示。

 

 

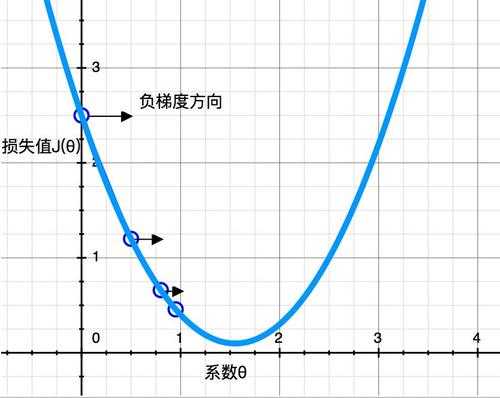
梯度下降中一个重要的参数是每一步的步长，取决于超参数学习率。如果学习率太低，算法需要经过大量迭代才能收敛，这将消耗很长时间；如果学习率太高，可能会直接跳过最小值，会导致算法发散，值越来越大，达不到实际的优化效果。

 

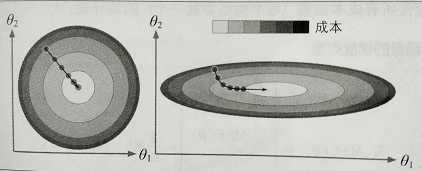
梯度下降会有陷阱。如下图所示，左边训练集上特征θ1和特征θ2具有相同的数值规模，收敛的就比较快；右边训练集上特征θ1的值就比特征θ2要小得多，先是沿着全局最小值方向近乎垂直方向前进，接下来一段是平坦的长长的山谷，会抵达最小值，但需要花费很长时间。

应用梯度下降或梯度上升时，需要保证所有特征值的大小比例都差不多（比如使用scikit-learn中的StandardScaler类），量纲不同时需要标准化处理，否则收敛的时间会非常久。

 

 

梯度下降步长

                        

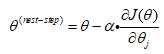
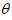：步长，求最小值

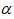：学习率

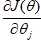：成本函数的偏导数

 

1.1.1  批量梯度下降

批量梯度下降，全称Batch Grandient Descent，简称BGD。

 

批量梯度下降每一步都使用整批训练集数据，面对非常庞大的训练集时，算法会变得极慢。

要找合适的学习率，可以使用网格搜索，但是需要限制迭代次数。如果设置太低，算法可能在离最优解还很远时就停了；如果设置得太高，模型达到最优解后，继续迭代参数不再变化，又会浪费时间。一个简单的办法是，在开始时设置一个非常大的迭代次数，但是当梯度向量的值变得很微小时中断算法-也就是它的范数变得低于ε（称为容差）时，这时梯度下降几乎达到了最小值。

                                                                                         

1.1.2  随机梯度下降

随机梯度下降，全称Stochastic Grandient Descent，简称SGD。

随机梯度下降在每一步训练集中随机选择一个实例，基于单个实例来计算梯度。这种算法的速度会快很多，但最终结果不一定是最小值。它可以逃出局部最优，但缺点是定位不出最小值。要解决这个困境，有一个办法是逐步降低学习率。开始的步长比较大（有助于快速进展和逃离局部最小值），然后越来越小，让算法尽量靠近全局最小值。这个过程叫做模拟退火。

 

1.1.3  小批量梯度下降

小批量梯度下降，全称Mini-Batch Grandient Descent，简称MBGD。

小批量梯度下降是基于一小部分的随机实例集来计算梯度。

 

1.1.4  算法比较

算法	数据集m很大	是否支持核外	特征数量n很大	超参数	是否需要缩放	scikit-learn
标准方程	快	否	慢	0	否	LinearRegression
BGD	慢	否	快	2	是	n/a
SGD	快	是	快	>=2	是	SGDRegressor
MBGD	快	是	快	>=2	是	n/a