马尔科夫状态转移矩阵

Posted 2022-08-16 yytxdy

　　状态转移矩阵是俄国数学家马尔科夫提出的，他在20世纪初发现：一个系统的某些因素在转移过程中，第n次结果只受第n-1的结果影响，即只与上一时刻所处状态有关，而与过去状态无关。 在马尔科夫分析中，引入状态转移这个概念。所谓状态是指客观事物可能出现或存在的状态；状态转移是指客观事物由一种状态转移到另一种状态

　　在状态转移矩阵中，矩阵各元素表示状态转移的概率，并且各行元素之和等于1，其现实意义是，各个状态的百分比总和为1

　　假定某大学有1万学生，每人每月用1支牙膏，并且只使用“中华”牙膏与“黑妹”牙膏两者之一。根据本月（12月）调查，有3000人使用黑妹牙膏，7000人使用中华牙膏。又据调查,使用黑妹牙膏的3000人中，有60%的人下月将继续使用黑妹牙膏，40%的人将改用中华牙膏； 使用中华牙膏的7000人中， 有70%的人下月将继续使用中华牙膏，30%的人将改用黑妹牙膏。据此，可以得到以下转移矩阵

　　

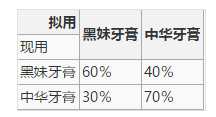
　　通过转移矩阵与初始化状态，即可预测之后月份两种牙膏的市场占比

　　代码实现如下：

　　

import matplotlib.pyplot as plt
import numpy as np


def markov():
    current_status = np.array([3000, 7000])
    transfer_matrix = np.array([[0.6, 0.4], [0.3, 0.7]])
    img_points = []
    for i in range(100):
        current_status = np.dot(current_status, transfer_matrix)
        img_points.append(current_status)
        print(i, "\\t", current_status)
    plt.plot(img_points)
    plt.show()


markov()

　　程序运行结果如下：

　　

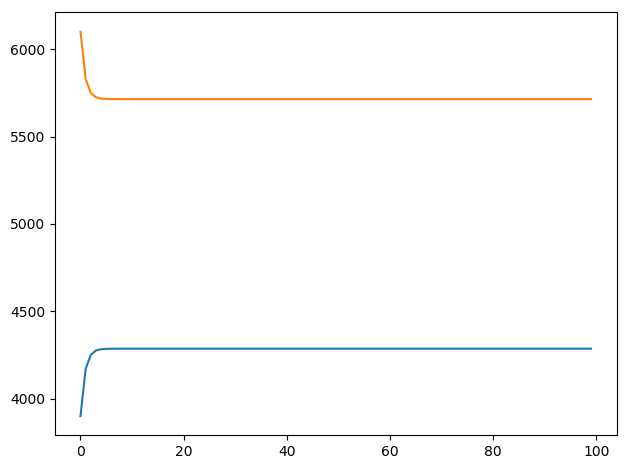
　　经过N次转换后，两种牙膏的市场占比趋于一个固定的数值：4285.71428571，5714.28571429