还是畅通工程 HDU - 1233Kruskal模板题

Posted 2022-08-15 keepz

Kruskal算法讲解

该部分内容全部摘录自刘汝佳的《算法竞赛入门经典》

Kruskal算法的第一步是给所有边按照从小到大的顺序排列。 这一步可以直接使用库函数
qsort或者sort。 接下来从小到大依次考查每条边(u,v)。
情况1： u和v在同一个连通分量中， 那么加入(u, v)后会形成环， 因此不能选择。
情况2： 如果u和v在不同的连通分量， 那么加入(u, v)一定是最优的。 为什么呢？ 下面用
反证法——如果不加这条边能得到一个最优解T， 则T+(u, v)一定有且只有一个环， 而且环中
至少有一条边(u‘ , v‘)的权值大于或等于(u,v)的权值。 删除该边后， 得到的新树T‘=T+(u, v)-(u‘,
v‘)不会比T更差。 因此， 加入(u, v)不会比不加入差。
下面是伪代码：

把所有边排序， 记第i小的边为e[i]（ 1<=i<m）
初始化MST为空
初始化连通分量， 让每个点自成一个独立的连通分量
for(int i = 0; i < m; i++)
if(e[i].u和e[i].v不在同一个连通分量) 
把边e[i]加入MST
合并e[i].u和e[i].v所在的连通分量

在上面的伪代码中， 最关键的地方在于“连通分量的查询与合并”： 需要知道任意两个点
是否在同一个连通分量中， 还需要合并两个连通分量。这就用到了并查集。可以把每个连通分量看成一个集合， 该集合包含了连通分量中的所有点。 这些点两两连通， 而具体的连通方式无关紧要， 就好比集合中的元素没有先后顺序之分， 只有“属于”和“不属于”的区别。 在图中， 每个点恰好属于一个连通分量， 对应到集合表示中， 每个元素恰好属于一个集合。 换句话说， 图的所有连通分量可以用若干个不相交集合来表示。
并查集的精妙之处在于用树来表示集合。 例如， 若包含点1， 2， 3， 4， 5， 6的图有3个
连通分量1,3、 2,5,6、 4， 则需要用3棵树来表示。 这3棵树的具体形态无关紧要， 只要
有一棵树包含1、 3两个点， 一棵树包含2、 5、 6这3个点， 还有一棵树只包含4这一个点即
可。 规定每棵树的根结点是这棵树所对应的集合的代表元（ representative） 。
如果把x的父结点保存在p[x]中（ 如果x没有父结点， 则p[x]等于x） ， 则不难写出“查找结
点x所在树的根结点”的递归程序： int find(int x) p[x] == x ? x : find(p[x]); ， 通俗地讲就是：
如果p[x]等于x， 说明x本身就是树根， 因此返回x； 否则返回x的父结点p[x]所在树的树根。
问题来了： 在特殊情况下， 这棵树可能是一条长长的链。 设链的最后一个结点为x， 则
每次执行find(x)都会遍历整条链， 效率十分低下。 看上去是个很棘手的问题， 其实改进方法
很简单。 既然每棵树表示的只是一个集合， 因此树的形态是无关紧要的， 并不需要在“查
找”操作之后保持树的形态不变， 只要顺便把遍历过的结点都改成树根的子结点， 下次查找
就会快很多了。

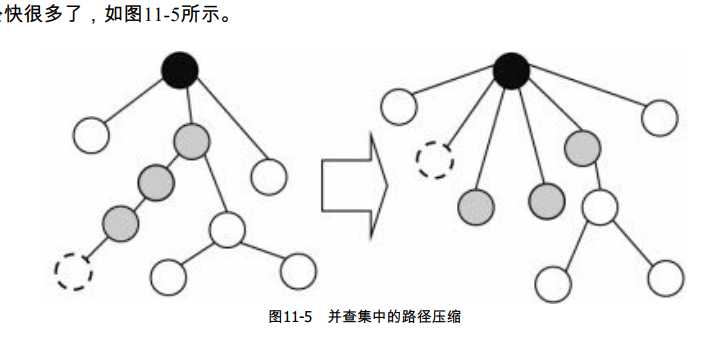
关于并查集的更深一步了解可以看一下这个博文。

题目讲解及AC代码

题目讲解

这个题目不难看出是个寻找最短路的问题，用Kruskal算法+并查集比较合适

AC代码

/*Kruskal算法*/
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long LL;
const int maxn = 100 + 10;
int N, father[maxn];
struct Road

    int _st, _en, _dist;
;
Road r[maxn*maxn];
bool cmp(Road a, Road b)

    return a._dist < b._dist;

int Find(int root)

    if(root != father[root])
        father[root] = Find(father[root]);
    return father[root];

int main()

//    freopen("input.txt", "r", stdin);
//    freopen("output.txt", "w", stdout);
    while(cin >> N && N)
    
        for(int i = 1; i <= N; i++)
            father[i] = i;
        for(int i = 0; i < N * (N - 1) / 2; i++)
            cin >> r[i]._st >> r[i]._en >> r[i]._dist;
        sort(r, r + N*(N-1)/2, cmp);
        int ans = 0;
        for(int i = 0; i < N * (N - 1) / 2; i++)
        
            int st_ = r[i]._st, en_ = r[i]._en;
            int x = Find(st_), y = Find(en_);
            if(x != y )
            
                ans += r[i]._dist;
                father[x] = y;
            
        
        cout << ans << endl;