噪音与误差

Posted 2022-08-12 redo19990701

误差测量

描述

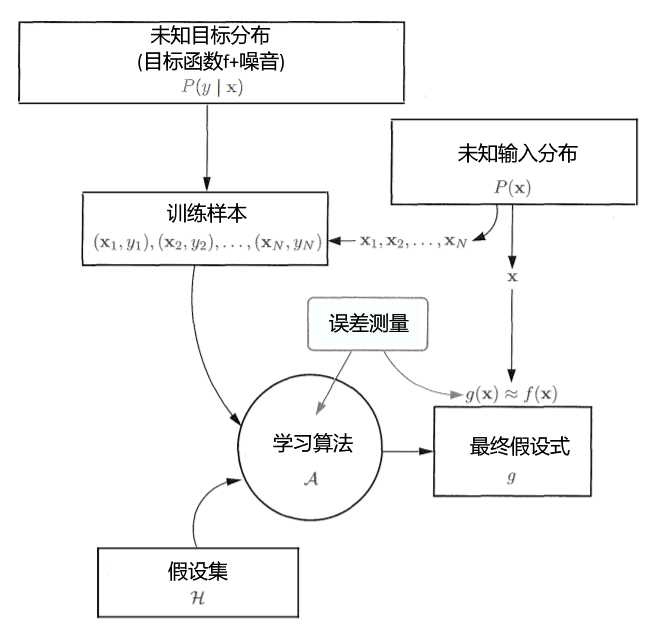
误差测量是描述一个假设式和目标函数的接近程度,以此为标准从假设集中挑选出最为接近的一个假设式h,即g作为最终假设式.

误差越小越接近目标函数

• 作用于一个样本点上的误差测量: e(h(x),f(x))
  • 平方误差: e(h(x),f(x))=(h(x)-f(x))\\(^2\\)
  • 二进制误差: e(h(x),f(x))=[[h(x)\\(\\neq\\)f(x))]]
    • 即假设式和目标函数产生结果不同的样本点数量
• 整体误差测量: E(h,f)
  • 逐点误差的平均值即为整体误差

样本内外误差

• 样本内误差(作用在样本空间内)
  • E\\(_in\\)(h)=\\(\\frac1N\\sum_1^Ne(h(x_n),f(x_n))\\)
• 样本外误差(所有样本点的误差的期望)
  • E\\(_out\\)(h)=\\(E_x[e(h(x_n),f(x_n))]\\)

误差分类

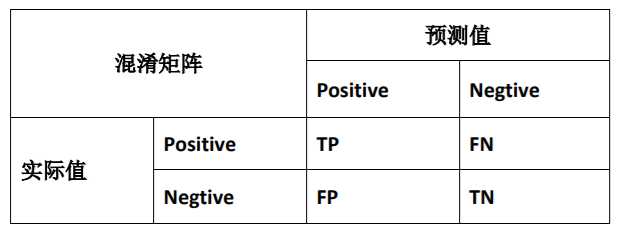
1. 正确肯定 (True Positive,TP)
2. 正确否定(True Nagtive,TN)
3. 错误肯定(False Positive,FP)
4. 错误否定(False Nagtive,FN)

正确肯定和正确否定都是没有误差的,错误肯定和错误否定是误差所在

不同情形下两种误差的付出的代价不同,

假如是安全局的指纹门,错误肯定(外人也可以进入,安全隐患)就会付出很大代价,而错误否定就没有很多事

假如是超市的vip卡,错误否定(是vip却识别为不是)就会让消费者很尴尬,代价较大,错误肯定就只是付出一点优惠而已

• 查准率(Precision)=TP/(TP+FP)
  • 描述了假设式的准确度(目标函数评定为+1的样本中假设式评定为+1的比率)
• 查全率(Recall)=TP/(TP+FN)
  • 描述了假设式的全面性(假设式评定为+1的样本中目标函数评定为+1的比率)
• 在权衡两者时可以使用F1值
  • F\\(_1\\) Score=2\\(\\fracPRP+R\\)

噪音

描述

即使相同的输入也有可能得到不同的输出(条件相同的两个人申请贷款很有可能得到不同的贷款额度),现实生活中目标函数往往是存在噪音的,并不是一成不变的

噪音分类

• 确定噪音(Deterministic noise)
  • 目标函数复杂度相较于假设式较高
  • 假设式不具有完全学习比自己复杂的目标函数的能力
• 随机噪音(Stochastic noise)
  • 样本中的坏点(即不正确的样本)
  • 坏点引导学习算法学习错误的信息