KMP算法

Posted 2022-08-12 ycx-akioi

KMP算法

KMP是一种字符串匹配算法。此算法的核心在于\\(kmp\\)数组以及它的求法。

（以下约定字符串下标从\\(1\\)开始）

\\(\\bmkmp\\)数组

定义\\(kmp\\)数组：\\(kmp_a,i\\)表示字符串\\(a\\)的前缀\\(a_1\\sim i\\)的最长相同真前后缀的长度，即\\(kmp_a,i=\\max\\limits_j\\in[0,i),a_1\\sim j=a_i-j+1\\sim i\\j\\\\)。显然，\\(kmp_a,1=0\\)恒成立。例如若\\(a=``\\textabacaabac''\\)，那么\\(kmp_a=[0,0,1,0,1,1,2,3,4]\\)。

\\(\\bmkmp\\)数组的求法

给定一个字符串\\(a\\)，现在我们要求\\(kmp_a\\)。

\\(\\forall i\\in(1,|a|]\\)，假设已经知道了\\(kmp_a,1\\sim i-1\\)，现在要求出\\(kmp_a,i\\)。考虑试试在\\(a_1\\sim i-1\\)的一组相同真前后缀的后面同时加上\\(1\\)个字符，看看这\\(2\\)个字符相不相同。设当前试的的为\\(a_1\\sim i-1\\)的长度为\\(now\\)的相同真前后缀。执行以下步骤：

1. 从最长的开始试起，即初始令\\(now=kmp_a,i-1\\)。

2. 如果往后加的\\(2\\)个字符（分别为\\(a_now+1,a_i\\)）相等的话，则匹配成功，直接令\\(kmp_a,i=now+1\\)并结束（因为比它长的相同真前后缀都试过了）；否则找次长一点的\\(a_1\\sim i-1\\)的相同真前后缀，不难发现\\(kmp_a,now\\)就是次长一点的长度（原因见下图），便令\\(now=kmp_a,now\\)。

   

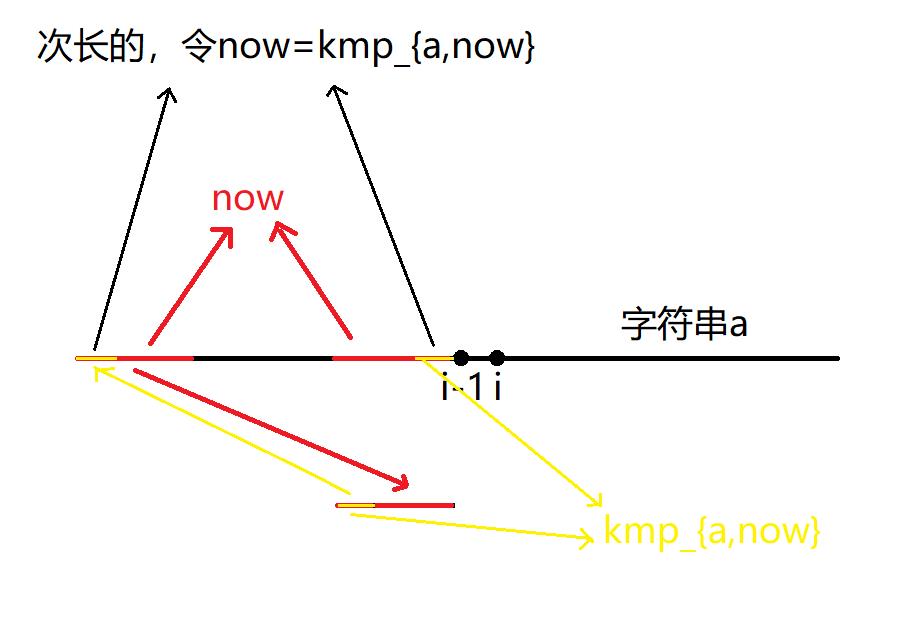
3. 不断重复第\\(2\\)步，如果中途没有结束，那么直到\\(now=0\\)的时候，令\\(kmp_a,i=[a_1=a_i]\\)并结束。

这样先令\\(kmp_a,1=0\\)，然后按上述方法从\\(i=2\\)到\\(i=|a|\\)递推，即可求出\\(kmp_a\\)。

求\\(kmp\\)数组的代码如下：（很短吧？很好写吧？很爽吧？

void kmp_init()//求kmp数组
    kmp[1]=0;//恒成立
    for(int i=2;i<=n;i++)//从i=2递推到i=n
        int now=kmp[i-1];//初始化now
        while(now&&c[now+1]!=c[i])now=kmp[now];//重复第2步
        if(c[now+1]==c[i])kmp[i]=now+1;
    

时间复杂度

上述方法求\\(kmp\\)数组的时间复杂度是是线性的\\(\\mathrm O(|a|)\\)。

证明：我们可以把\\(now\\)看成一个定义在for外面的变量来研究它的增减，kmp[i]=now+1;可理解成now++;，因为下一轮循环的时候就会执行now=kmp[i-1];。不难发现，for里的第\\(2\\)行while会使\\(now\\)进行不增变化（也就是可能不变，可能减少），第\\(3\\)行会使\\(now\\)增加\\(0\\sim 1\\)。那么\\(now\\)增加\\(1\\)的次数为\\(\\mathrm O(|a|)\\)，于是\\(now\\)减少也只能有\\(\\mathrm O(|a|)\\)次机会了。所以总共就是\\(\\mathrm O(|a|)\\)了。

KMP算法的应用

KMP算法可以用来字符串模式匹配（这个Z算法和哈希也能做到线性复杂度）。看到网上很多blog都是用\\(kmp\\)数组来优化暴力匹配，但我有更好理解的方法（复杂度不变）。与Z算法类似，我们可以把模式串\\(b\\)隔一个不常用字符接到文本串\\(a\\)前面，即令\\(c=b+`\\text!'+a\\)。然后求出\\(kmp_c\\)，从\\(i=|b|+2\\)到\\(i=|c|\\)扫一遍，如果\\(kmp_c,i=|b|\\)，那么在\\(a\\)的\\(i-|b|+1\\)处匹配成功。

不仅如此，如果想专门求字符串\\(a\\)的某前缀的最长相同真前后缀的长度，哈希的复杂度就无异于暴力了（因为匹配成败没有单调性，不好二分）。Z算法稍微好一点，\\(\\forall i\\in[1,|a|]\\)，令\\(\\forall j\\in [1,z_a,i],ans_i+j-1=\\max(ans_i+j-1,j)\\)，这个可以用差分或线段树实现，复杂度都带\\(\\log\\)，没有KMP的线性复杂度好。