大白话5分钟带你走进人工智能-第35节神经网络之sklearn中的MLP实战
Posted lhworldblog
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了大白话5分钟带你走进人工智能-第35节神经网络之sklearn中的MLP实战相关的知识，希望对你有一定的参考价值。
本节的话我们开始讲解sklearn里面的实战：
先看下代码：
from sklearn.neural_network import MLPClassifier
X = [[0, 0],
[1, 1]]
y = [0, 1]
clf = MLPClassifier(solver=‘sgd‘, alpha=1e-5, activation=‘logistic‘,
hidden_layer_sizes=(5, 2), max_iter=2000, tol=1e-4)
clf.fit(X, y)
predicted_value = clf.predict([[2, 2],
[-1, -2]])
print(predicted_value)
predicted_proba = clf.predict_proba([[2., 2.],
[-1., -2.]])
print(predicted_proba)
print([coef.shape for coef in clf.coefs_])
print([coef for coef in clf.coefs_])
我们依次解释下：
在sklearn里面，我们需要
这样来导入神经网络这个模块，如果做分类，就是MLPClassifier，它和神经网络什么关系？它叫做多层感知机。这里是用它做分类的一个算法。
接下来
人为地构建了一个数据集， X矩阵里面有两行两列， Y是构建了两行一列，分别是分类号，负例和正例。
如何使用多层感知机呢？
先创建一个对象MLPClassifier：
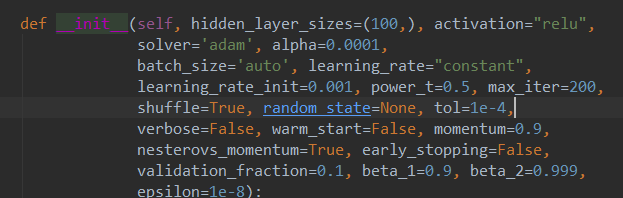
解释下这些参数：solver就是选择最优解的算法，随机梯度下降SGD；alpha是L2正则前面的超参数；activation=logistic意味着每一个神经元最后的function是Sigmoid函数；max_iter是最大迭代次数，如果迭代次数达到2000次，我们就把2000的结果作为最优解；tol是收敛的阈值，如果在2000次内达到了阈值，就停了。
我们再来看下MLP的源码参数：
?
学习率是learning_rate，如果是constant就是一直保持学习率的值，如果是invscaling就是根据公式来每次迭代算学习率。
activation如果是logistic，就是sigmod函数；如果是tanh，就是-1到+1；如果是relu，就是max(0,z)，平时用的时候就是这些个。
最关键的是hidden_layer_sizes隐藏层的节点数：
（5,2）意思是有两个隐藏层，第一个隐藏层有五个神经元，第二个隐藏层有两个神经元。为什么要写成（5,2）？因为如果第一个隐层H1有五个神经元，第二层有两个神经元，这两个隐藏层之间要算多少个连线的w呢？就是五行两列，十个连线上的w。可以直接计算出来。
MLP多层感知机，它其实就只是全连接，如果你不是全连接它就不能叫多层感知机了，而sklearn里面只有多层感知机。
它是层与层之间的网络拓扑，x数据里面有两个x，相当于第一个输入层有两个神经元x1，x2。我们把隐藏层设五个隐藏节点，所以隐藏里分类点就有5个。所以输入层到第一个隐藏层的w矩阵，它的形状是两行五列。
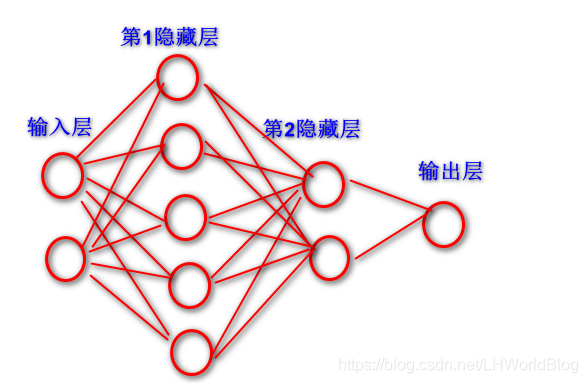
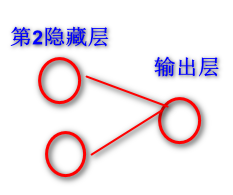
第二个隐藏层设置是两个神经元，第二个w矩阵就是五行两列，因为这里是做一个二分类， Y的标签里面就两个类别号，所以它是做二分类，二分类需要一个输出节点就够了。所以最后一个矩阵它是两行一列。以下是这个网络拓扑结构图：
?
fit后就可以来计算出来最终的w参数、模型。
有了分类器这个模型，我们就可以通过predict进行预测：
意思是未来给它一个x，它可以给你y。预测结果如下：
predicted_value是两行一列的，如果用的是predicted_proba，有什么区别呢？
在sklearn里面，用predicted_proba，它给出的是概率值，打印结果如下：
Clf.coefs_，就是把这些w全部拿出来，然后for循环这些w，它是分层的。然后看shape，就可以清晰地知道，从输入层到第一个隐藏层，中间网络拓扑是什么样子的，然后第一个隐藏层到第二个隐藏层，以此类推。如果我们直接把coef的打印输出的话，我们就可以直接拿到层与层之间的w矩阵具体值是什么样子的。结果如下：
我们从线性代数矩阵相乘的概念去解释最后的输出：
x数据集是一个两行两列的数据：
输入层和第一个隐藏层之间w矩阵是两行五列的
?
它们点积两行两列*两行五列=两行五列的数据。判断是两行五列之后，还要再跟第一个隐藏层和第二个隐藏层之间五行两列的w矩阵相乘，
?
得到的就是两行五列*五行两列=两行两列的结果，最后和两行一列的相乘：
?
得到的是两行两列*两行一列=两行一列的?，因为x是两行，所以最后得到的是两个?。
完美~~~解释！！哈哈。
真正去做predict时候，就是把某一条数据带起来，分别做一个正向传播，如果用predict，结果和0.5比较进行判别，给出分类号；如果是predict_proba它不用根据0.5进行判别，直接输出概率。
不管数据量有多少，只要写的是SGD，就会在每次迭代的时候选x数据集里面的一部分数据来进行训练，因为总共2000次迭代，迭代次数越多，相当于所有的数据都会被随机到。
总结下神经网络需要考虑三件事情：第一个是设置激活函数，第二个是设置网络拓扑，就是构建一个神经网络时，它有多少层，然后每一层有神经元的个数。这里是做分类的，输入和输出层不用设置，输入层、输出层有多少神经元，根据它有多少个x，和y多少个分类，它就会自动设置神经元。把网络拓扑定下来，第三就是需要去设置有多少个隐藏层，每层有多少个神经元，那么一个元组来表达（5,2），告诉这里有两个隐藏层，数值是每个隐藏有多少个神经元。一百层就是元组里有一百个数。比如三个隐藏层（10,8,15），意思是第一个隐藏层10个神经元，第二个隐藏层8个神经元，第三个隐藏层15个神经元。里面的值是随便定的。怎么设置是没有方法设置，这个是调的，咱们的工作。后期深度学习里面咱们说案例，都会去判别它的准确率，然后根据准确率判别有没有过拟合，在深度学习里面都会奔着过拟合的方向去调，如果过拟合再往回调。比如设置100个隐藏层，我发现50个隐藏层的效果跟100个一样，那么就设置50个，训练得更快，使用的时候正向传播也更快，这个值是调的。不同的应用方向，比如卷积神经网络或者循环神经网络，参数设置是有一些规律的，它但是没有一个死的数，还是根据规律来调的。
激活函数是统一设置的，在神经网络拓扑里面，每一个神经元的激活函数都是一样的，都是统一的，在神经网络里面是这样，在深度学习里面也是这样。假如设置了ReLU，隐藏层，输出层，激活函数都是ReLU，如果是Sigmoid，它都是Sigmoid。对于sklearn来说，就必须得是统一的。
对于tensorflow来说，它给了更多的自由度，可以让每一层都是一样的，但是层与层之间可以设置不一样的。
下面进入Q&A环节：
w矩阵的顺序是什么样的，也就是每一层和每一层之间的w的形状是什么样的？
比如有两个隐藏层，第一个隐藏层H1有五个神经元，第二个隐藏层H2有两个神经元，连接一定是5*2有10个连接，w矩阵就是五行两列的。
每个神经元的位置谁放上，谁放下无所谓。因为中间的隐藏节点，它具体代表什么含义是我们不管的，因为我们没法知道它具体代表什么含义。
以上是关于大白话5分钟带你走进人工智能-第35节神经网络之sklearn中的MLP实战的主要内容，如果未能解决你的问题，请参考以下文章
大白话5分钟带你走进人工智能-第二十五节决策树系列之信息增益和信息增益率
大白话5分钟带你走进人工智能-第十八节逻辑回归之交叉熵损失函数梯度求解过程