后缀数组(理解)
Posted -citywall123
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了后缀数组(理解)相关的知识,希望对你有一定的参考价值。
一、基本概念
后缀:用 suff[i] 表示,是指从某个位置 i 开始到整个串末尾结束的一个子串。
后缀数组:用 sa[i] 表示,是指所有后缀在排完序后,排名为i的后缀在原串中的位置。 sa[排名]=位置
名次数组:用 rank[i] 表示,是指所有后缀在排序完后,原字符串中第i个后缀现在的排名。 rank[位置]=排名
比如字符串aabaaaab$,(我们习惯在字符串后面加一个特殊字符$,表示字符串的结尾)他的所有后缀、位置、排名如下:
后缀 位置 排名
suff[ 1 ] : aabaaaab$ sa[ 4 ] = 1 rank[ 1 ]=4
suff[ 2 ] : abaaaab$ sa[ 6 ] = 2 rank[ 2 ]=6
suff[ 3 ] : baaaab$ sa[ 8 ] = 3 rank[ 3 ]=8
suff[ 4 ] : aaaab$ sa[ 1 ] = 4 rank[ 4 ]=1
suff[ 5 ] : aaab$ sa[ 2 ] = 5 rank[ 5 ]=2
suff[ 6 ] : aab$ sa[ 3 ] = 6 rank[ 6 ]=3
suff[ 7 ] : ab$ sa[ 5 ] = 7 rank[ 7 ]=5
suff[ 8 ] : b$ sa[ 7 ] = 8 rank[ 8 ]=7
字符串大小的比较
字符串的比较是逐位按字典序比较,若字典序相同,则比较下一位,否则直接分出大小
1、b<aaaaaaaaaaaaaaaaaaaa
2、aab<aabc
二、倍增法求后缀数组

注意:
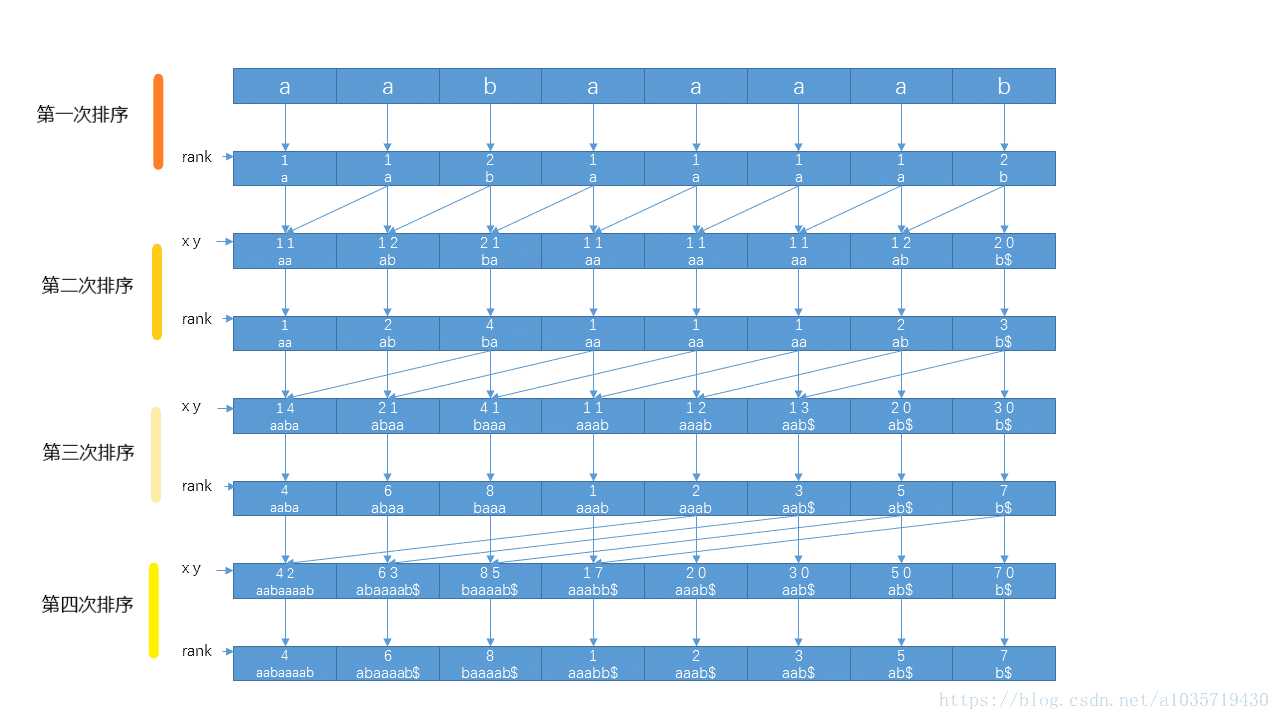
上面通过排名来比较字符串的大小,采用的是基数排序的方法,这里介绍一下基数排序
时间复杂度:O(len),len是字符串的长度
所谓基数排序,就是从最低位开始,先按个位排,再排十位,再排百位……,若出现相等,则把先出现的数视为较小,放在前面
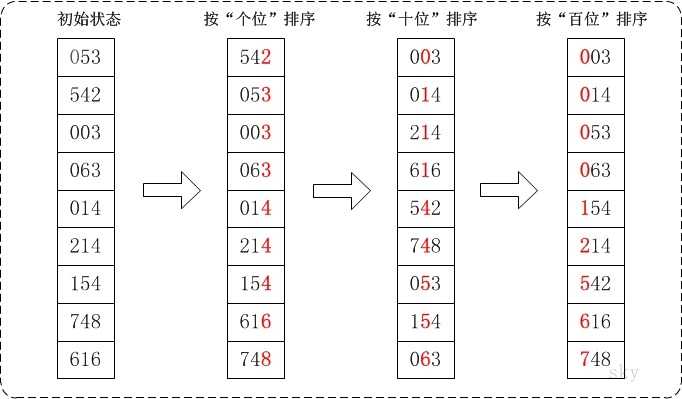
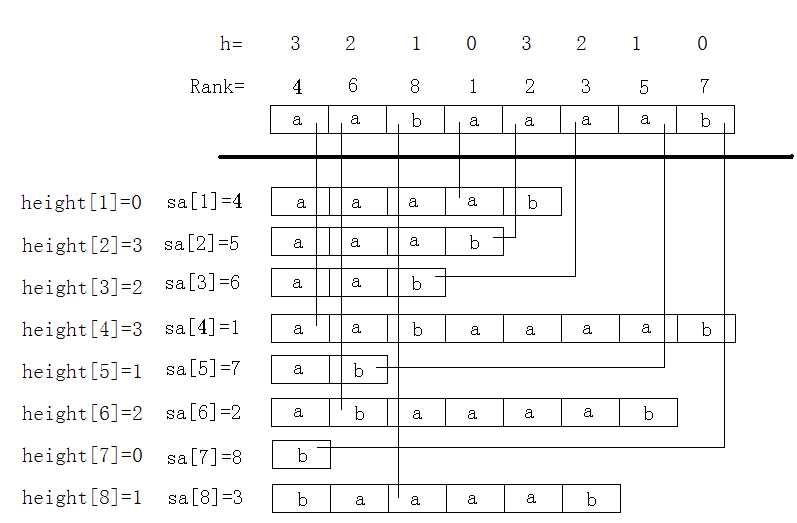
三、最长公共前缀--LCP
height[i]:表示suff[sa[i]]和suff[sa[i−1]]的最大公共前缀,也就是排名完后两个相邻的后缀的最长公共前缀。
四、代码
代码的实现过程还不太懂,先把板子记下来
#include<iostream> #include<string.h> #include<string> #include<algorithm> #include<math.h> #include<string> #include<string.h> #include<vector> #include<utility> #include<map> #include<queue> #include<set> #define mx 0x3f3f3f3f #define ll long long using namespace std; const int N = 1e6 + 10; int num = 122, len; int fir[N], sec[N], t[N], sa[N],height[N]; //first[]相当于是rank数组,first[i]表示从位置i开始到结尾的后缀排名是first[i]; first[位置]=排名 //sa[i]表示排名为i的后缀的起始位置是从sa[i]开始到结尾的 //height[i]表示排名为i的后缀和排名为i-1的后缀的最长公共前缀的长度是height[i] char s[N]; inline void SA() for (int i = 1; i <= num; ++i) t[i] = 0; for (int i = 1; i <= len; ++i) ++t[fir[i] = s[i]]; for (int i = 1; i <= num; ++i) t[i] += t[i - 1]; for (int i = len; i >= 1; --i) sa[t[fir[i]]--] = i; for (int k = 1; k <= len; k <<= 1) int cnt = 0; for (int i = len - k + 1; i <= len; ++i) sec[++cnt] = i; for (int i = 1; i <= len; ++i) if (sa[i] > k) sec[++cnt] = sa[i] - k; for (int i = 1; i <= num; ++i) t[i] = 0; for (int i = 1; i <= len; ++i) ++t[fir[i]]; for (int i = 1; i <= num; ++i) t[i] += t[i - 1]; for (int i = len; i >= 1; --i) sa[t[fir[sec[i]]]--] = sec[i], sec[i] = 0; swap(fir, sec); fir[sa[1]] = 1, cnt = 1; for (int i = 2; i <= len; ++i) fir[sa[i]] = (sec[sa[i]] == sec[sa[i - 1]] && sec[sa[i] + k] == sec[sa[i - 1] + k]) ? cnt : ++cnt; if (cnt == len) break; num = cnt; void Getheight() int j, k = 0; //目前height数组计算到k for (int i = 1; i <= len; i++) if(k) k--; //由性质得height至少为k-1 int j = sa[fir[i] - 1]; //排在i前一位的是谁 while(s[i + k] == s[j + k]) k++; height[fir[i]] = k; int main() scanf("%s", s + 1);//字符串是从位置1开始读入 len = strlen(s + 1); SA(); Getheight(); for (int i = 1; i <= len; ++i) //输出排名为i的起始位置的下标 printf("%d\\n", sa[i]); // for(int i=1;i<=len;i++)//从小到大输出字符串s的所有后缀 // // for(int j=sa[i];j<=len;j++) // cout<<s[j]; // cout<<endl; // cout<<"--------------"<<endl; for(int i=1;i<=len;i++)//位置从左往右输出所有后缀的排名 cout<<fir[i]<<endl; cout<<"-------------"<<endl; for(int i=1;i<=len;i++)//输出相邻后缀的最长公共前缀长度 cout<<height[i]<<endl; return 0;
以上代码转载自https://www.cnblogs.com/lykkk/p/10520070.html,里面详细的介绍了代码的实现过程,有时间在详细理解,orz
以上是关于后缀数组(理解)的主要内容,如果未能解决你的问题,请参考以下文章