数据结构——LCA小结

Posted 2022-08-07 konglingyi

·丧

写法一、树上倍增

·倍增：以2^k为步来走

·说明：

Dep[v]记录节点v的深度（层数）
fa[v][k]记录节点v向上第2k个祖先的编号
·预处理：
fa[v][k]=fa[fa[v][k-1]][k-1]；

·向上走（Go_up）的实现：

s为倍增的上限，比如这个树的总层数为8，则s为3（23==8）

从v号点向上走p层(伪代码)

Go_up(v,p) 

For(int i=0;i<S;i++)
 If(P&(1<<i)) v=fa[v][i];
                        // O(logN)　　

此处利用奇妙的二进制与运算。举个例子来说明：

5的二进制：  1 0 1

         对应k：2 1 0

      对应2^k：4 0 1

显然，4+1=5.

i=0, (p&(1<<i))==(101&1)2==1 , v=fa[v][0]
i=1, (p&(1<<i))==(101&10)2==0
i=2, (p&(1<<i))==(101&100)2==1 , v=fa[v][2]

故通过这种写法，可以实现向上跳格子~

·LCA原理：

假设x是u和v的最近公共祖先
1.x往上到根的路径上的所有点都是u和v的公共祖先；
所以当fa[u][i]==fa[v][i]条件成立时，fa[u][i]不一定是它们的最近公共祖先。

2.若fa[u][i]!=fa[v][i],说明点fa[u][i]和点fa[v][i]一定是x下方的点。

求u和v公共祖先(伪代码)

Lca(u, v)  // dep[u]<dep[v]
Go_up(v,dep[v]-dep[u]);
For(int i=S;i>=0;i--)
If(fa[u][i]!=fa[v][i])  u=fa[u][i],v=fa[v][i]; 
Return fa[v][0];
 // O(logN)

·于是精妙且复杂的板子就可以搞出来了：

#include<cstdio>
#include<iostream>
#include<cmath>
using namespace std;
const int maxn = 500005;
const int maxe = 1000005;
int n,m,root;

struct line
	int from,to;
	line()//空构造函数 line p; 
	line(int A,int B)
		//构造函数 line L=line(1,2);
		from=A;to=B;
	
;
line edge[maxe];
int last[maxn],_next[maxe],e; 

//last[x]表示以x为起点的最后一条边（的编号） 
//_next[i]表示与第i条边起点相同的上一条边（的编号） 

////////////////////////////////////////
void add_edge(int x,int y)
	edge[++e]=line(x,y);
	_next[e]=last[x];
	last[x]=e;

////////////////////////////////////////疑难处1 

int Fa[maxn][35],Dep[maxn];
void dfs(int x,int fa)
	int i,k,y;
	Fa[x][0]=fa;
	Dep[x]=Dep[Fa[x][0]]+1;                       //记录当前节点的深度 
	k=ceil(log(Dep[x])/log(2));                      //x往上倍增的上限 
	for(i=1;i<=k;i++)Fa[x][i]=Fa[Fa[x][i-1]][i-1];  //倍增计算祖先 
	
	///////////////////////////////////////////
	for(int i=last[x];i/*i>0*/;i=_next[i])
		int v=edge[i].to;
		if(v!=fa)dfs(v,x); 
	//////////////////////////////////////////疑难处2
	 
	

int LCA(int x,int y)
	int i,k,s;
	s=ceil(log(n)/log(2));                 //该树倍增最大可能的上限 
	if(Dep[x]<Dep[y])swap(x,y);      //交换x和y的值 
/////////////x往上走k层，让x与y处于同一层 //////////
	k=Dep[x]-Dep[y];
	
	/////////////////////////////////////////////////// 
	for(i=0;i<=s;i++)
	    if(k&(1<<i))x=Fa[x][i];//Go-up:k为进位，当k&(1<<i)==1时，说明向上走2^i步 
	//x==y时，x就是最近公共祖先
	///////////////////////////////////////////////////疑难处3 
	
	if(x==y)return x;                      
///////////////////////////////////////////////////
	s=ceil(log(Dep[x])/log(2));           //计算向上倍增的上限 
	for(i=s;i>=0;i--)
	    if(Fa[x][i]!=Fa[y][i]) x=Fa[x][i]; y=Fa[y][i]; 
	return Fa[x][0];


int main()
	int i,j,k;
	cin>>n>>m>>root;
	for(i=1;i<n;i++)
		int x,y;
		scanf("%d%d",&x,&y);
		add_edge(x,y);
		add_edge(y,x);
	
	dfs(root,0);
	for(i=1;i<=m;i++)
		int x,y;
		scanf("%d%d",&x,&y);
		printf("%d\\n",LCA(x,y));
	
		
 

·压轴—重要的图解说明：

---

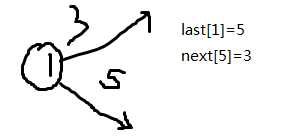
写法二、树链剖分

·树链剖分：

树链剖分，或者叫轻重链剖分，是一种把树变成链的方法.
size[]表示每个点的子树的大小.
dep[]表示每个点的深度.
Son[]表示每个点儿子中子树最大的那个儿子.
所有节点p和它的Son[p]连接的为重链，其他的边为轻链.
top[]表示每个点所在的重链的最上面的节点.
这几个数组可以通过两次dfs求出来.

 

现在之前的变量都求出来了，怎么求两个节点的LCA？
对于两个点x, y：
case1：他们的top相同，说明他们在同一个重链上，所以dep比较小的那个就是LCA.
case2：他们的top不同，则选择top深度比较深的那个往上跳.
时间复杂度：预处理为O(n)，查询一次为O(logn).

·LCA代码：

void dfs(int p, int fa) 
	tr[p].sz = 1;
	for (int x = first[p]; x; x = e[x].next)
		if (e[x].to != fa) 
			int y = e[x].to;
			tr[y].dep = tr[p].dep + 1;
			dfs(y, p);
			tr[p].sz += tr[y].sz;
			if (tr[p].son == 0 || tr[y].sz > tr[tr[p].son].sz)
				tr[p].son = y;
		


void DFS(int p, int fa) 
	if (tr[p].son != 0) 
		tr[tr[p].son].top = tr[p].top;
		DFS(tr[p].son, p);
	
	for (int x = first[p]; x; x = e[x].next)
		if (e[x].to != fa && e[x].to != tr[p].son) 
			y = e[x].to;
			tr[y].top = y;
			DFS(y, p);
		


int lca(int x, int y) 
	while (tr[x].top != tr[y].top) 
		if (tr[tr[x].top].dep < tr[tr[y].top].dep)
			swap(x, y);
		x = tr[tr[x].top].fa;
	
	if (tr[x].dep < tr[y].dep) swap(x, y);
	return y;