Codeforces Round #578 (Div. 2)

Posted 2022-08-01 acmerszl

Solution

---

A. Hotelier

题意：
对应\\(n\\)个位置，如果是\\(L\\)，左边第一个为\\(0\\)的位置变为\\(1\\)，如果是\\(R\\)，右边第一个为\\(0\\)的位置变为\\(1\\)，如果是数字，对应位置变为\\(0\\)。
思路：
模拟即可。但是比赛就是无语，这么辣鸡的题目，竟然用数字判字符\\(0\\)……

//#define DEBUG
#include<bits/stdc++.h>
using namespace std;
#define lson (rt<<1)
#define rson (rt<<1|1)
const int N=100010;
const int inf=0X3f3f3f3f;
const long long INF = 0x3f3f3f3f3f3f3f3f;
const double eps = 1e-6;
const double pi = acos(-1.0);
const int mod = 1000000007;
typedef long long ll;
 
char s[N];
int a[15];
int main() 
    int n;
    scanf("%d",&n);
    scanf("%s",s);
    int l=0,r=9;
    for(int i=0;i<n;i++) 
        //printf("%c %d %d***\\n",s[i],l,r);
        if(s[i]=='L') 
            a[l]=1;
         else if(s[i]=='R') 
            a[r]=1;
         else a[s[i]-'0']=0;
        for(int j=0;j<10;j++) 
            if(a[j]==0) 
                l=j;
                break;
            
        
        for(int j=9;j>=0;j--) 
            if(a[j]==0) 
                r=j;
                break;
            
        
        //for(int j=0;j<10;j++) printf("%d ",a[j]);
        //puts("");
    
    for(int i=0;i<10;i++) printf("%d",a[i]);

B. Block Adventure

题意：
一个角色去冒险，有个无穷大的背包，初始有\\(m\\)个木块，然后路上都是高度为\\(h_i\\)的木桩，他站在木桩上，只要下一个木桩与当前高度差\\(\\leq\\ k\\)，你就能上去，当然你擅长木工，你可以用背包里的木块使当前木桩变高，也可以每次削减当前木桩高度为1的木块任意次，（但不能为使当前木桩高度为负）。问你是否可以到达最后的木桩。
思路：
很明显贪心，每次尽量取最多的木块放入背包。做这个题的时候很傻，刚开始由于这么定位置，然后用列方程搞定，但是只是脑子里去判的正负，没有根据\\(x\\)的具体值操作，导致自闭。

• 如果\\(h_i+1>h_i 并且 h_i+1-h_i>k+m\\)，显然不行了。若能够到达下一个，要分是增高还是削减，可以列方程\\(x=h_i+1-h_i-k\\)，若\\(x>0\\)，说明要增高\\(x\\)，\\(m\\)要消耗\\(x\\)，若\\(x\\leq0\\)，则判断是否削减高度大于自身高度，处理即可。

• 如果\\(h_i+1\\leq\\ h_i\\)，肯定是削减高度，判断是否削减高度大于自身高度。
  比赛改了半年emmmm，最后3分钟网页炸了，\\(37\\)秒的时候文件提交晚了，赛后\\(AC\\)

//#define DEBUG
#include<bits/stdc++.h>
using namespace std;
#define lson (rt<<1)
#define rson (rt<<1|1)
const int N=100010;
const int inf=0X3f3f3f3f;
const long long INF = 0x3f3f3f3f3f3f3f3f;
const double eps = 1e-6;
const double pi = acos(-1.0);
const int mod = 1000000007;
typedef long long ll;
 
int h[110];
int main() 
    int _,n,k;
    ll m;
    for(scanf("%d",&_);_;_--) 
        scanf("%d%lld%d",&n,&m,&k);
        ll res=m;
        for(int i=1;i<=n;i++) 
            scanf("%d",&h[i]);
        
        int i;
        for(i=1;i<n;i++) 
            int zhi;
            if(h[i]<h[i+1]) 
                if(h[i+1]-h[i]-k>res) break;
                zhi=h[i+1]-h[i]-k;
                if(zhi>0) res-=zhi;
                else 
                    zhi*=-1;
                    if(h[i]>zhi) res+=zhi;
                    else res+=h[i];
                
             else 
                zhi=(k+h[i]-h[i+1]>h[i])?h[i]:k+h[i]-h[i+1];
                res+=zhi;
            
        
        if(i<n) puts("NO");
        else puts("YES");
    

C. Round Corridor

题意：
两个圆盘，内圈\\((1,1),\\ldots,(1,n)\\)，外圈\\((2,1),\\ldots,(2,m)\\)，等分。询问\\((s_x,s_y)\\)是否能到达\\((e_x,e_y)\\)。

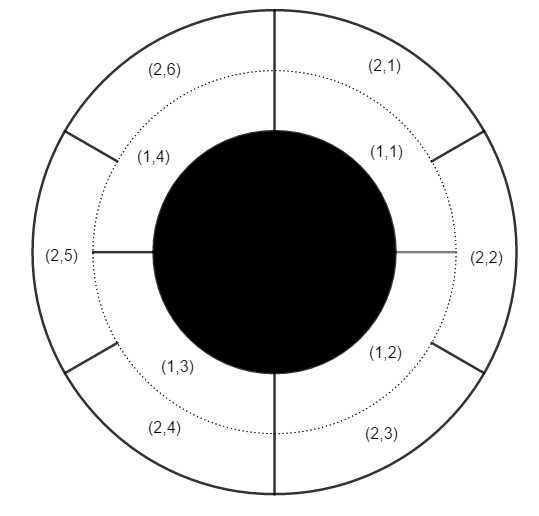
很明显，当\\(n,m\\)互质时，必定可以到达，如果不互质，画几个情况，可以发现可以把区域分组，然后判断即可。

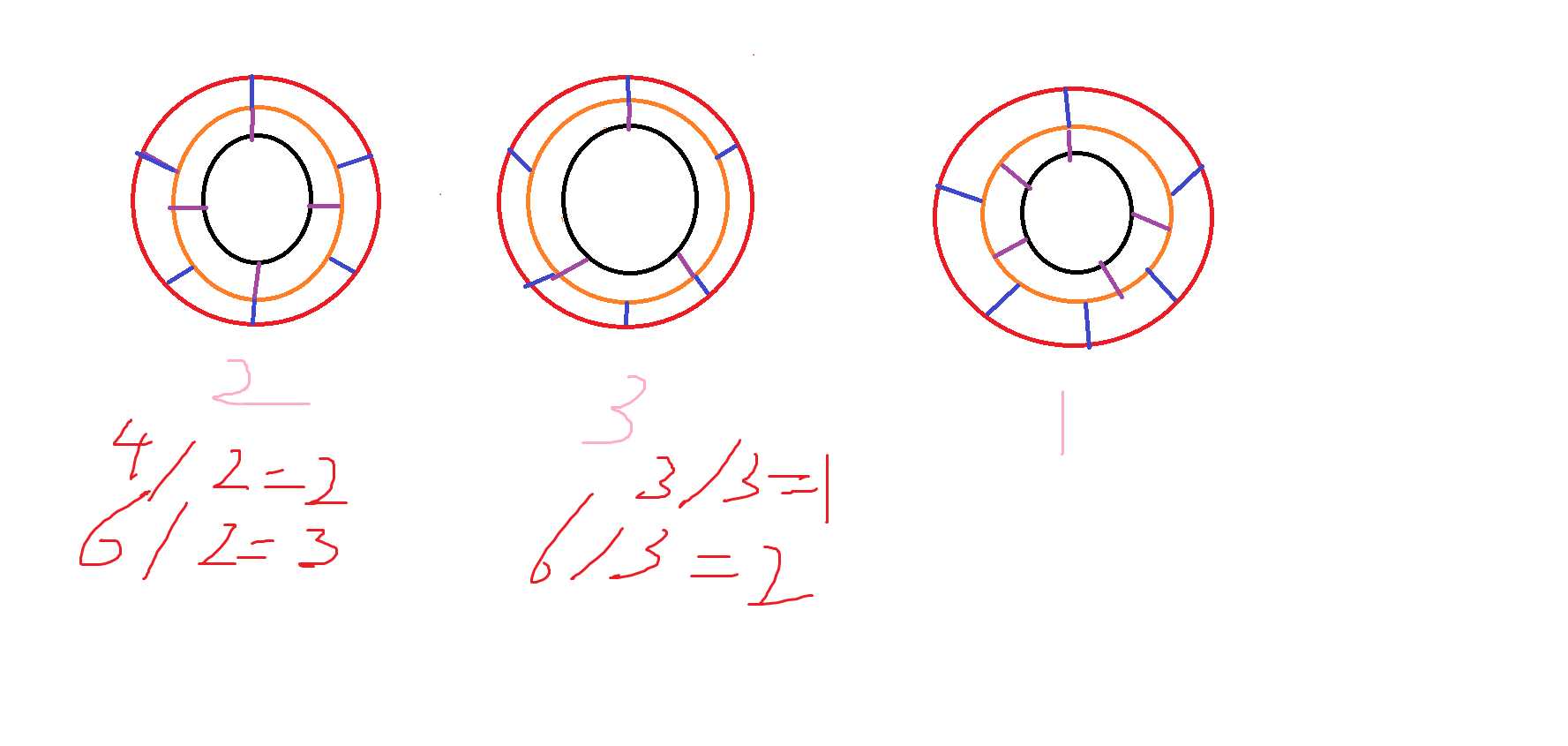
如果是同一圈的判断，可以判断是否是同一组，如果不是同一圈的，可以先根据内圈的第几组算出对应外圈可以达到的范围，再\\(check\\)一下即可。

//#define DEBUG
#include<bits/stdc++.h>
using namespace std;
#define lson (rt<<1)
#define rson (rt<<1|1)
const int N=3000010;
const int inf=0X3f3f3f3f;
const long long INF = 0x3f3f3f3f3f3f3f3f;
const double eps = 1e-6;
const double pi = acos(-1.0);
const int mod = 1000000007;
typedef long long ll;
 
ll n,m,q;
int main() 
    scanf("%lld%lld%lld",&n,&m,&q);
    ll tmp=__gcd(n,m);
    while(q--) 
        ll x,a,y,b;
        scanf("%lld%lld%lld%lld",&x,&a,&y,&b);
        if(tmp==1) 
            puts("YES");
            continue;
        
        ll partn=n/tmp,partm=m/tmp;
        bool ok=false;
        if(x==y) 
            ll part=(x==1)?partn:partm;
            if(ceil(a*1.0/part)==ceil(b*1.0/part)) ok=true;
         else 
            ll tmpcal=(x==1)?a:b;
            ll tmpcheck=(x==1)?b:a;
            ll r=ceil(tmpcal*1.0/partn)*partm;
            ll l=r-partm+1;
            if(tmpcheck>=l&&tmpcheck<=r) ok=true;
        
        if(ok) puts("YES");
        else puts("NO");
    

D. White Lines

题意：
给出\\(n\\times\\ n\\)的黑白块矩形，然后你可以最多使用一次\\(k\\times\\ k\\)的橡皮擦，你若选中\\(ceil(i,j)\\)，那么以该块作为左上角的\\(k\\times\\ k\\)的矩形块可变为白色，求操作后最多有几条白色条状（一行或一列都为白色即为白色条状）
思路：
首先从行考虑，若都为白色，直接计入答案。否则判断最左和最右的长度是否\\(\\leq k\\)，不是的话，没有贡献，若是的话，把所有能覆盖这段的块贡献+1。考虑列也是相同作法，然后求所有块的最大值即可。但是增加贡献用直接赋值的话，复杂度O(n_3)，不过好像能过。我们可以用二维差分的思想来求

再次学习差分思想+前缀和。

• 一维差分，令\\(d_i=a_i-a_i-1\\)，然后可以根据\\(d\\)数组，得到\\(a\\)数组，因为\\(a_i=d_1+d_2+,\\ldots,+d_i\\)，即原数组等于差分数组的前缀和
  即\\(a_i=(a_1-a_0)+(a_2-a_1)+,\\ldots,+(a_i-a_i-1)\\)
  若将\\(a\\)数组\\(L\\sim\\ R+x\\)，只需\\(d_L+x,d_R-x\\)即可。见图
  

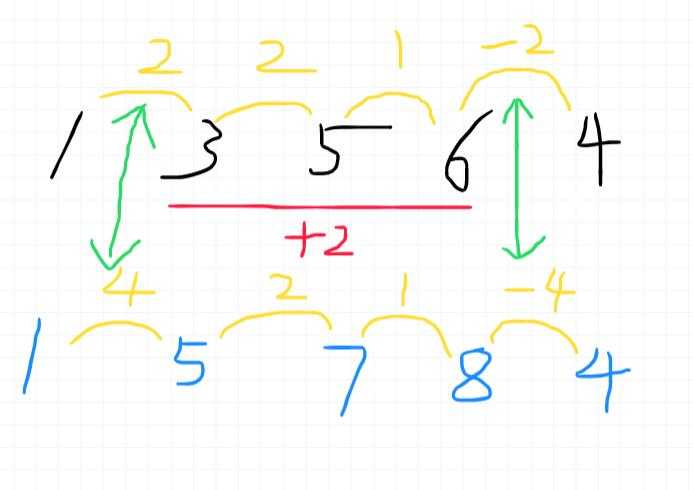
• 二维的我们也可以差分。
  
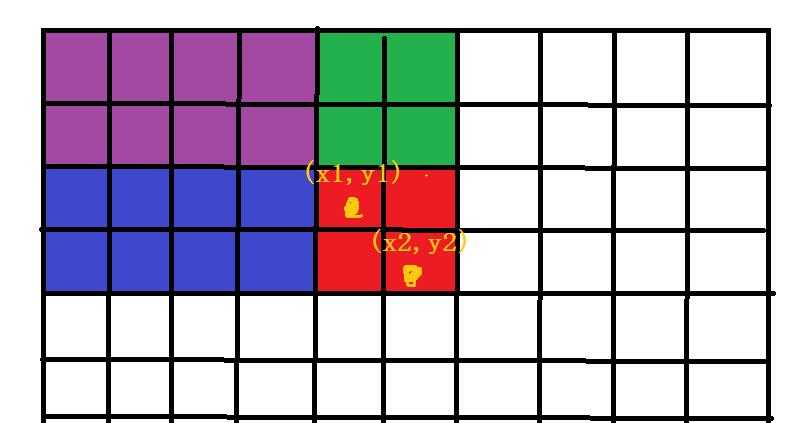
  求红色矩阵的面积，首先二维前缀和处理出到左上角的面积。然后\\(S_红=S_整个面积-(S_蓝+S_紫)-(S_绿+S_紫)+S_紫\\)
  对应公式就是\\(sum[x_2][y_2]-sum[x_2][y_1-1]-sum[x_1-1][y_2]+sum[x_1-1][y_1-1]\\)。
  其中\\(sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+a[i][j]\\)

考虑一维差分是从区间开始位置和结束位置修改，对于二维：

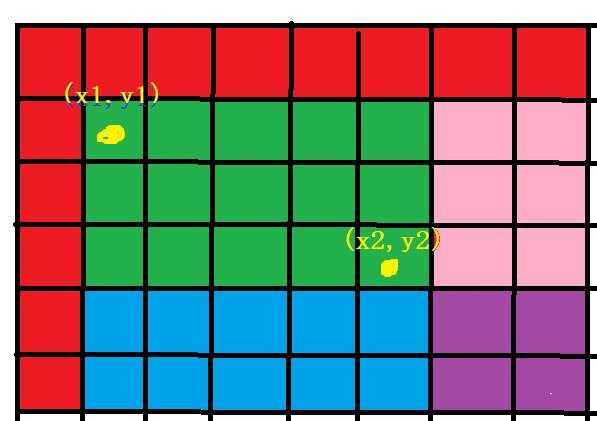
若将绿色部分增加\\(x\\)，我们可以这样修改\\(a[x_1][y_1]+=x,a[x_2+1][y_1]-=x,a[x_1][y_2+1]-=x,a[x_2+1][y_2+1]+=x\\)，
若将\\((x_1,y_1)+=x\\),那么一直到右下角都会被影响，所以我们可以让蓝色部分一直到右下角都减\\(x\\)，粉色部分一直到右下角都减\\(x\\)，这样紫色部分多减了一次，我们让紫色部分再加\\(x\\)，即可。
然后根据差分性质，求二维前缀和即可知道每一个位置的值。

对于这道题，我们可以求出有贡献的矩形范围，然后差分思想修改，最后二维前缀和取每个位置最大值即可。

//#define DEBUG
#include<bits/stdc++.h>
using namespace std;
#define lson (rt<<1)
#define rson (rt<<1|1)
const int N=100010;
const int inf=0X3f3f3f3f;
const long long INF = 0x3f3f3f3f3f3f3f3f;
const double eps = 1e-6;
const double pi = acos(-1.0);
const int mod = 1000000007;
typedef long long ll;
 
char g[2010][2010];
int dif[2010][2010];
 
int main() 
    #ifdef DEBUG
    freopen("in.txt","r",stdin);
    #endif
    int n,k,sum=0;
    scanf("%d%d",&n,&k);
    for(int i=1;i<=n;i++) 
        scanf("%s",g[i]);
    
    for(int i=1;i<=n;i++) 
        int st=-1,ed=-1;
        for(int j=0;j<n;j++) 
            if(g[i][j]=='B') 
                if(st==-1) st=j+1;
                ed=j+1;
            
        
        if(st==-1) sum++;
        else if(ed-st+1<=k) 
            int lx=max(1,i-k+1),ly=max(1,ed-k+1);
            int rx=i,ry=st;
            dif[lx][ly]++;
            dif[lx][ry+1]--;
            dif[rx+1][ly]--;
            dif[rx+1][ry+1]++;
        
    
    for(int j=0;j<n;j++) 
        int st=-1,ed=-1;
        for(int i=1;i<=n;i++) 
            if(g[i][j]=='B') 
                if(st==-1) st=i;
                ed=i;
            
        
        if(st==-1) sum++;
        else if(ed-st<=k) 
            int lx=max(1,ed-k+1),ly=max(1,j+1-k+1);
            int rx=st,ry=j+1;
            dif[lx][ly]++;
            dif[lx][ry+1]--;
            dif[rx+1][ly]--;
            dif[rx+1][ry+1]++;
        
    
    int ans=-1;
    for(int i=1;i<=n;i++) 
        for(int j=1;j<=n;j++) 
            dif[i][j]=dif[i][j]+dif[i][j-1]+dif[i-1][j]-dif[i-1][j-1];
        
    
    for(int i=1;i<=n;i++) 
        for(int j=1;j<=n;j++) 
            ans=max(ans,dif[i][j]);
        
    
    printf("%d\\n",sum+ans);

E. Compress Words

题意：
压缩单词，前面后缀和后面前缀有公共部分就压缩。
思路：
\\(KMP\\)裸题，不过文本串匹配位置可以用最大压缩位置开始，发现之前的题白做了，复习一下\\(KMP\\)。

\\(Next[i]\\)表示\\(i\\)之前，前缀和后缀相同的最大值。
比如\\(ababc\\)，\\(Next\\)数组为\\(\\-1,0,0,1,2\\\\)

简要梳理，\\(Next\\)数组的求法，根据模式串与模式串匹配递推得出。
如果\\(t[i]==t[j]\\)，那么\\(Next[++i]=++j\\)，意会emmm

匹配就不相等\\(j=Next[j]\\)，相等就都后移。

这道题就直接匹配，返回的\\(j\\)值，即能匹配成功的最后位置的下一位。

//#define DEBUG
#include<bits/stdc++.h>
using namespace std;
#define lson (rt<<1)
#define rson (rt<<1|1)
const int N=100010;
const int inf=0X3f3f3f3f;
const long long INF = 0x3f3f3f3f3f3f3f3f;
const double eps = 1e-6;
const double pi = acos(-1.0);
const int mod = 1000000007;
typedef long long ll;
 
int n;
string ans;
string s;
 
int Next[N*10];
void prekmp(string s) 
    int j=Next[0]=-1;
    int i=0;
    int len=s.size();
    while(i<len) 
        while(j!=-1&&s[i]!=s[j]) j=Next[j];
        Next[++i]=++j;
    

 
int kmp(int pos) 
    int i=pos,j=0;
    int lenans=ans.size();
    while(i<lenans) 
        if(j==-1||ans[i]==s[j]) 
            i++;
            j++;
         else j=Next[j];
    
    return j;

 
int main() 
    #ifdef DEBUG
    freopen("in.txt","r",stdin);
    #endif
    scanf("%d",&n);
    cin>>ans;
    for(int i=2;i<=n;i++) 
        cin>>s;
        prekmp(s);
        int pos=kmp(max(0,(int)ans.size()-(int)s.size()));
        for(int j=pos;j<s.size();j++) ans+=s[j];
    
    cout<<ans<<'\\n';