Crt and ExCrt
Posted liuz8848
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Crt and ExCrt相关的知识,希望对你有一定的参考价值。
\\(Crt\\)
求解不定方程组
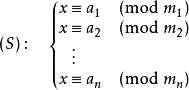
设\\(M=\\prod\\limits_i^nm_i\\)
\\(M_i=\\fracMm_i=\\prod\\limits_k,k\\neq i^nm_k\\)
\\(t_i\\)为\\(M_i\\)在模\\(m_i\\)时的逆元
先上结论 通解为\\(\\sum\\limits_i^na_iM_it_i mod LCM(m_i)\\)
证明:
对于方程组中第\\(i\\)个方程考虑
\\(\\because M_k(k\\neq i) mod m_i=0\\)
\\(\\therefore \\sum\\limits_k,k\\neq i^na_kM_kt_k\\equiv0 (mod m_i)\\)
又\\(\\because t_iM_i\\equiv1 (mod m_i)\\)
\\(\\therefore a_iM_it_i\\equiv a_i (mod m_i)\\)
$\\therefore \\sum\\limits_i^na_iM_it_i\\equiv a_i (mod m_i) $
解合法
得证,通解为\\(\\sum\\limits_i^na_iM_it_i mod LCM(m_i)\\)
void exgcd(int a,int b,int &x,int &y)
if(b==0) x=1; y=0; return;
exgcd(b,a%b,x,y);
int tp=x;
x=y; y=tp-a/b*y;
int china()
int ans=0,lcm=1,x,y;
for(int i=1;i<=k;++i) lcm*=b[i];
for(int i=1;i<=k;++i)
int tp=lcm/b[i];
exgcd(tp,b[i],x,y);//求逆元
x=(x%b[i]+b[i])%b[i];//x要为最小非负整数解
ans=(ans+tp*x*a[i])%lcm;
return (ans+lcm)%lcm;
ExCrt
扩展中国剩余定理解决的是\\(m_i\\)不互质的问题
不再是宏观上直接构造一个通解,因为它的通解无法直接用公式表示
用归纳法,考虑前\\(k-1\\)个方程的通解为\\(x(mod M), M=LCM(m_1到m_k-1)\\)
我们为了符合第\\(k\\)个方程,需要加一些数,但为了保证前\\(k-1\\)个方程仍然成立,所以只能加若干倍的\\(M\\),也就是说找到\\(x+t*M\\equiv a_k(mod m_k)\\)
上式整理得\\(t*M\\equiv a_k-x(mod m_k)\\)
可以用扩展欧几里得求解,若同余方程无解则整个方程组无解
否则新的解为\\(x+t*M(mod LCM(M,m_k))\\)
有一些细节对代码解释
lt exgcd(lt a,lt b,lt &x,lt &y)
if(b==0)x=1;y=0;return a;
lt gcd=exgcd(b,a%b,x,y);
lt tp=x;
x=y; y=tp-a/b*y;
return gcd;
lt excrt()
lt x,y,k;
lt M=bi[1],ans=ai[1];//一开始赋为初始值
for(int i=2;i<=n;i++)
lt a=M,b=bi[i],c=(ai[i]-ans%b+b)%b;//注意取模保证是正数
lt gcd=exgcd(a,b,x,y),bg=b/gcd;//t*M-y*mk=gcd,gcd为M和mk的gcd
if(c%gcd!=0) return -1; //因为求解是根据gcd而不是c,所以还要乘倍数,如果不是倍数证明无解
x=mul(x,c/gcd,bg);//将x乘倍数,这里取模mk/gcd的原因是x(也就是t)还要乘M,乘M之后不能超过LCM(M,mk),也就是不能超过M*m/gcd,所以这里直接对m/gcd取模即可
ans+=x*M;//答案更新
M*=bg;//模数更新
ans=(ans%M+M)%M;//处处取模小心负数
return (ans%M+M)%M;
以上是关于Crt and ExCrt的主要内容,如果未能解决你的问题,请参考以下文章