树的存储森林的存储

Posted 2022-07-28 sunbr

树的存储：

　　二叉树的存储：

　　　　1.  连续存储(顺序存储)【完全二叉树】，以数组实现

　　　　　　优点:

　　　　　　　　查找某个节点的父节点和子节点(包括判断有没有子节点和父节点)

　　　　　　缺点：

　　　　　　　　耗用内存空间过大

 

　　　　2.  链式存储：

　　　　　　一个节点包含三个部分：左子节点地址、数据域、右子节点地址

　　　　　　优点：耗内存小

 

　　一般树的存储：

　　　　　　由于计算机的内存是线性的，而树是非线性的。若在计算机里只存树的有效节点，便不能查找某个节点的子节点和父节点(或者说整个树的逻辑存储无法知晓)，所以必须要先转化成完全二叉树，把垃圾节点补上。

 

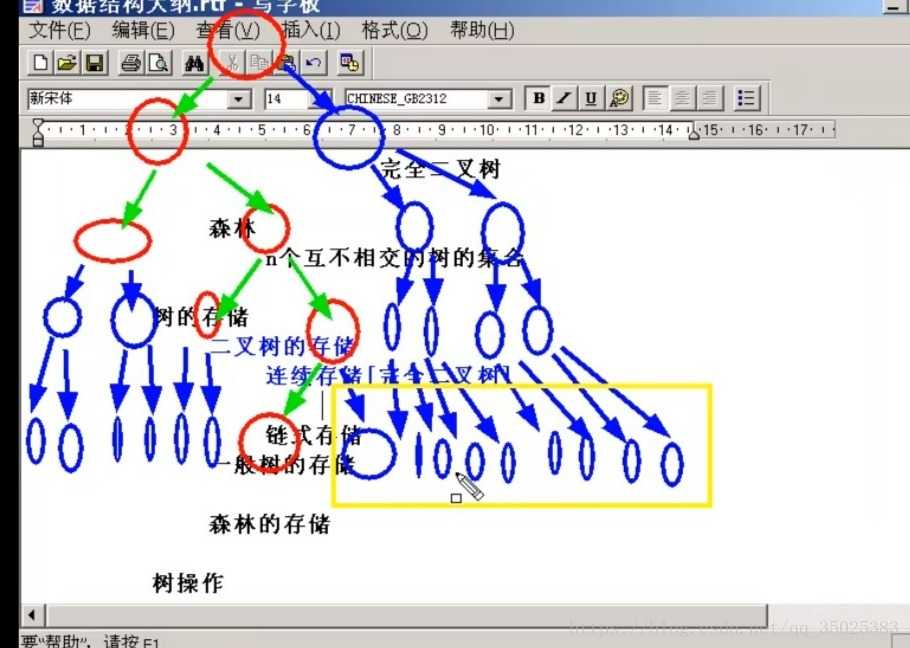
绿色的是普通树，蓝色的是转为满二叉树，黄色的是去掉了底层连续的叶子节点，即成了完全二叉树

 

　　双亲表示法：

由于树中的每个结点都有唯一的一个双亲结点，所以可用一组连续的存储空间（一维数组）存储树中的各个结点，数组中的一个元素表示树中的一个结点，每个结点含两个域，数据域存放结点本身信息，双亲域指示本结点的双亲结点在数组中位置(下标)。方便查询某结点的父结点

 

 

 

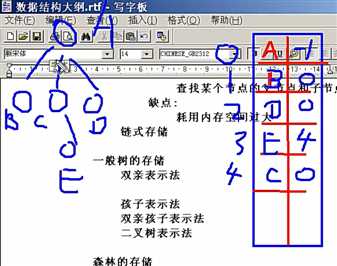
　　孩子表示法：

将树中的每个结点的孩子结点排列成一个线性表，用链表存储起来。对于含有 n 个结点的树来说，就会有 n 个单链表，将 n 个单链表的头指针存储在一个线性表中，这样的表示方法就是孩子表示法。如果结点没有孩子（例如叶子结点），那么它的单链表为空表。方便查询某结点的子节点

 

 

 

 

 

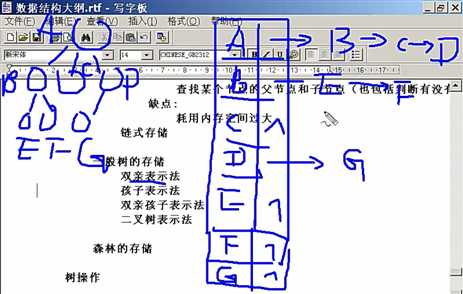
双亲孩子表示法：

　　方便查询某结点的子节点和父节点

 

 

 

 

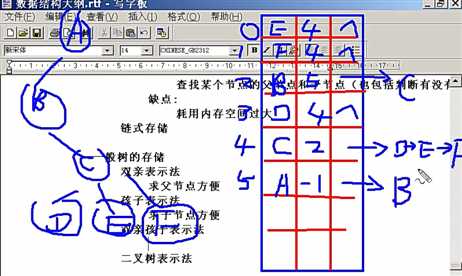
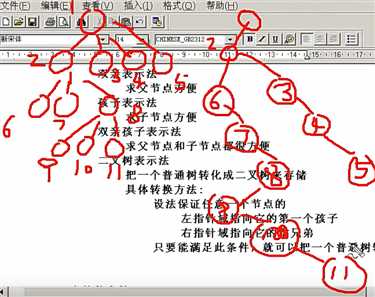
二叉树表示法(孩子兄弟表示法)：

把一个普通树转化成二叉树来存储，此二叉树的根节点没有右子树

使用链式存储结构存储普通树。链表中每个结点由 3 部分组成：

 

其中孩子指针域，表示指向当前结点的第一个孩子结点，兄弟指针域表示指向当前结点的下一个兄弟结点。

 

 

森林的存储：

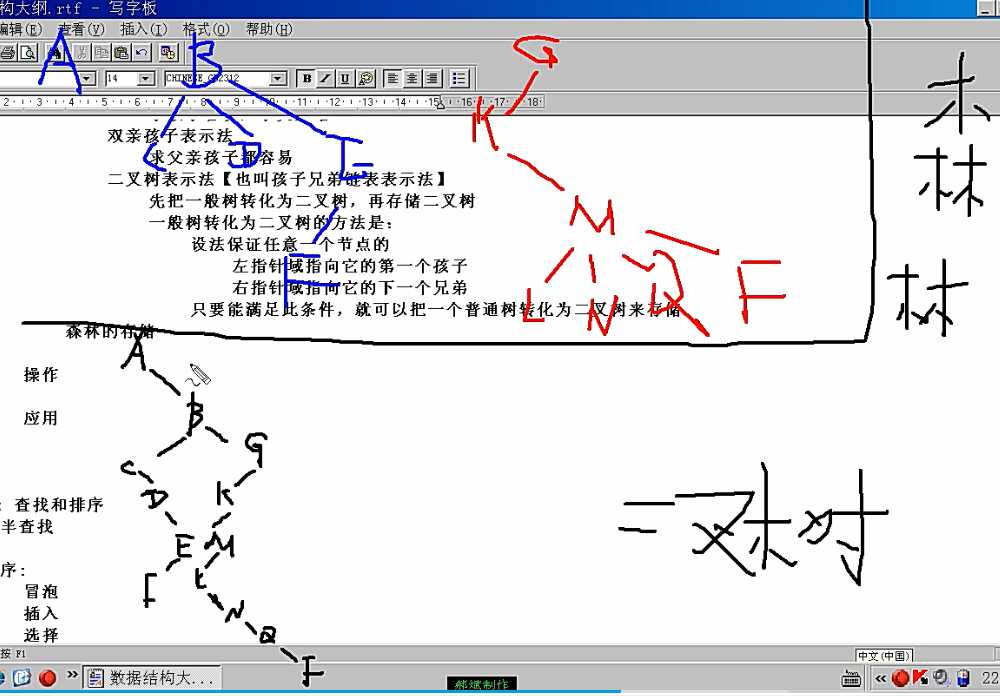
先把森林转化为二叉树，再存储二叉树

跟一般树转化为二叉树的过程相似，把不相交的根节点视为兄弟节点