floyd类型题UVa-10099-The Tourist Guide +Frogger POJ - 2253

Posted 2022-07-19 ofshk

The Tourist Guide

 Mr. G. works as a tourist guide. His current assignment is to take some tourists from one city to another. Some two-way roads connect the cities. For each pair of neighboring cities there is a bus service that runs only between those two cities and uses the road that directly connects them. Each bus service has a limit on the maximum number of passengers it can carry. Mr. G. has a map showing the cities and the roads connecting them. He also has the information regarding each bus service. He understands that it may not always be possible for him to take all the tourists to the destination city in a single trip. For example, consider the following road map of 7 cities. The edges connecting the cities represent the roads and the number written on each edge indicates the passenger limit of the bus service that runs on that road.

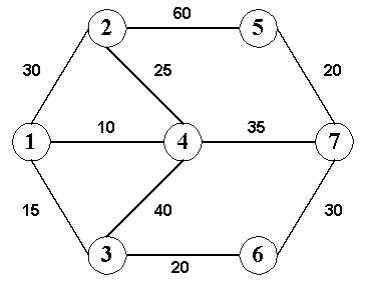
Now, if he wants to take 99 tourists from city 1 to city 7, he will require at least 5 trips and the route he should take is : 1 - 2 - 4 - 7. But, Mr. G. finds it difficult to find the best route all by himself so that he may be able to take all the tourists to the destination city in minimum number of trips. So, he seeks your help.

Input

The input will contain one or more test cases. The first line of each test case will contain two integers: N (N ≤ 100) and R representing respectively the number of cities and the number of road segments. Then R lines will follow each containing three integers: C1, C2 and P. C1 and C2 are the city numbers and P (P > 1) is the limit on the maximum number of passengers to be carried by the bus service between the two cities. City numbers are positive integers ranging from 1 to N. The (R + 1)-th line will contain three integers: S, D and T representing respectively the starting city, the destination city and the number of tourists to be guided. The input will end with two zeroes for N and R.

Output

For each test case in the input first output the scenario number. Then output the minimum number of trips required for this case on a separate line. Print a blank line after the output of each test case.

 1 #include<stdio.h>
 2 #include<string.h>
 3 #include<algorithm>
 4 #include<iostream>
 5 using namespace std;
 6 const int N=110;
 7 #define inf 0x3f3f3f3f
 8 int e[N][N];
 9 //int n;
10 
11 //void init(int nn)
12 //
13 //    for(int i=1; i<=nn; i++)
14 //    
15 //        for(int j=1; j<=nn; j++)
16 //        
17 //            if(i==j)
18 //                e[i][j]=0;
19 //            else
20 //                e[i][j]=inf;
21 //        
22 //    
23 //
24 
25 
26 int main()
27 
28     int n,m;
29     int tt=1;
30     while(~scanf("%d %d",&n,&m))
31     
32         //   init(n);
33         if(n==0&&m==0)
34             break;
35         memset(e,0,sizeof(e));
36         int aa,bb,cc;
37         for(int i=1; i<=m; i++)
38         
39             scanf("%d %d %d",&aa,&bb,&cc);
40             e[aa][bb]=e[bb][aa]=cc-1;
41             //  e[aa][bb]=e[bb][aa]=cc;
42         
43         for(int k=1; k<=n; k++)
44         
45             for(int i=1; i<=n; i++)
46             
47                 for(int j=1; j<=n; j++)
48                 
49                     //         if(e[i][j]!=inf&&e[i][k]!=inf&&e[k][j]!=inf)
50                     //     e[i][j]=max(e[i][j],e[i][k]+e[k][j]);
51                     e[i][j]=max(e[i][j],min(e[i][k],e[k][j]));
52                 
53             
54         
55 //        int tt=1;
56         //  cout<<e[1][7]<<"***"<<endl;
57         int a,b,c;
58         scanf("%d %d %d",&a,&b,&c);
59         int ans=(c-1)/e[a][b];
60         //  int ans=c/(e[a][b]-1);
61         if((c-1)%e[a][b]!=0)
62             //   if(c%e[a][b]!=0)
63             ans++;
64         //   ans=ans*2-1;
65         printf("Scenario #%d\\n",tt++);
66         printf("Minimum Number of Trips = %d\\n\\n",ans);
67     
68     return 0;
69 

 

 

Frogger

Freddy Frog is sitting on a stone in the middle of a lake. Suddenly he notices Fiona Frog who is sitting on another stone. He plans to visit her, but since the water is dirty and full of tourists‘ sunscreen, he wants to avoid swimming and instead reach her by jumping. 
Unfortunately Fiona‘s stone is out of his jump range. Therefore Freddy considers to use other stones as intermediate stops and reach her by a sequence of several small jumps. 
To execute a given sequence of jumps, a frog‘s jump range obviously must be at least as long as the longest jump occuring in the sequence. 
The frog distance (humans also call it minimax distance) between two stones therefore is defined as the minimum necessary jump range over all possible paths between the two stones. 

You are given the coordinates of Freddy‘s stone, Fiona‘s stone and all other stones in the lake. Your job is to compute the frog distance between Freddy‘s and Fiona‘s stone. 

Input

The input will contain one or more test cases. The first line of each test case will contain the number of stones n (2<=n<=200). The next n lines each contain two integers xi,yi (0 <= xi,yi <= 1000) representing the coordinates of stone #i. Stone #1 is Freddy‘s stone, stone #2 is Fiona‘s stone, the other n-2 stones are unoccupied. There‘s a blank line following each test case. Input is terminated by a value of zero (0) for n.

Output

For each test case, print a line saying "Scenario #x" and a line saying "Frog Distance = y" where x is replaced by the test case number (they are numbered from 1) and y is replaced by the appropriate real number, printed to three decimals. Put a blank line after each test case, even after the last one.

Sample Input

2
0 0
3 4

3
17 4
19 4
18 5

0

Sample Output

Scenario #1
Frog Distance = 5.000

Scenario #2
Frog Distance = 1.414

 1 #include<iostream>
 2 #include<string.h>
 3 #include<cmath>
 4 #include<iomanip>
 5 #define inf 0x3f3f3f3f
 6 using namespace std;
 7 
 8 //点点之间的距离floyd
 9 //找a-b所有路径中最大步数里面最小的
10 struct edge
11 
12 //    double x;
13 //    double y;
14     int x;
15     int y;
16  e[220];
17 
18 double a[220][220];
19 int n;
20 
21 double d(int x1,int y1,int x2,int y2)
22 
23     return sqrt(((x2-x1)*(x2-x1)*1.0+(y2-y1)*(y2-y1)*1.0)*1.0);
24 
25 
26 void init()
27 
28     for(int i=1;i<=n;i++)
29     
30         for(int j=1;j<=n;j++)
31         
32             if(i==j)
33                 a[i][j]=0;
34             else
35                 a[i][j]=inf;
36         
37     
38 
39 
40 int main()
41 
42     std::ios::sync_with_stdio(false);
43     cin.tie(0);
44     cout.tie(0);
45     int tt=1;
46     while(cin>>n)
47     
48         if(n==0)
49             break;
50         memset(e,0,sizeof(e));
51         memset(a,0,sizeof(a));
52         init();
53         for(int i=1; i<=n; i++)//n个顶点
54             cin>>e[i].x>>e[i].y;
55 
56    //     p=1;//p条边
57 
58         for(int i=1; i<=n; i++)
59         
60             for(int j=i+1; j<=n; j++)
61             
62               //  addedge[p++]=d(e[i].x,e[i].y,e[j].x,e[j].y);
63 
64                 double dd=d(e[i].x,e[i].y,e[j].x,e[j].y);
65                 if(a[i][j]>dd||a[j][i]>dd)
66                 
67                     a[j][i]=a[i][j]=dd;
68                 
69             
70         
71         //  sort(addedge+1,addedge+p+1,cmp1);
72         for(int k=1;k<=n;k++)
73         
74             for(int i=1;i<=n;i++)
75             
76                 for(int j=1;j<=n;j++)
77                 
78                     //if(a[i][j]a[i][k]+a[k][j])
79                         a[i][j]=min(a[i][j],max(a[i][k],a[k][j]));
80                 
81             
82         
83         double dis=a[1][2];
84         cout<<"Scenario #"<<tt++<<endl;
85         cout<<"Frog Distance = ";
86         cout<<setiosflags(ios::fixed)<<setprecision(3)<<dis<<endl<<endl;
87     
88     return 0;
89