二叉树——堆

Posted 2022-07-13 maider

一、堆的性质

　　结构性：用数组表示的完全二叉树

　　有序性：任意一结点的关键字是其子树所有结点的最大值（或最小值）

二、最大堆的操作

1、创建一个空的最大堆，堆从下标为1的地方开始存放（根结点下标为1）

2、最大堆的插入

首先，把要插入的结点放在数组的末尾，假设下标为H->size + 1

再将它与父结点比较，如果它比父结点大，两者互换位置

直到它比父结点小，这时候下标为0的很大的元素起到了哨兵作用。

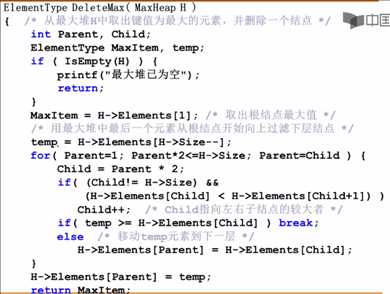
3、最大堆的删除：删除最大的元素，然后再调整剩余结点，使其仍然是一个最大堆

把最大堆的最后一个元素a挪到根结点

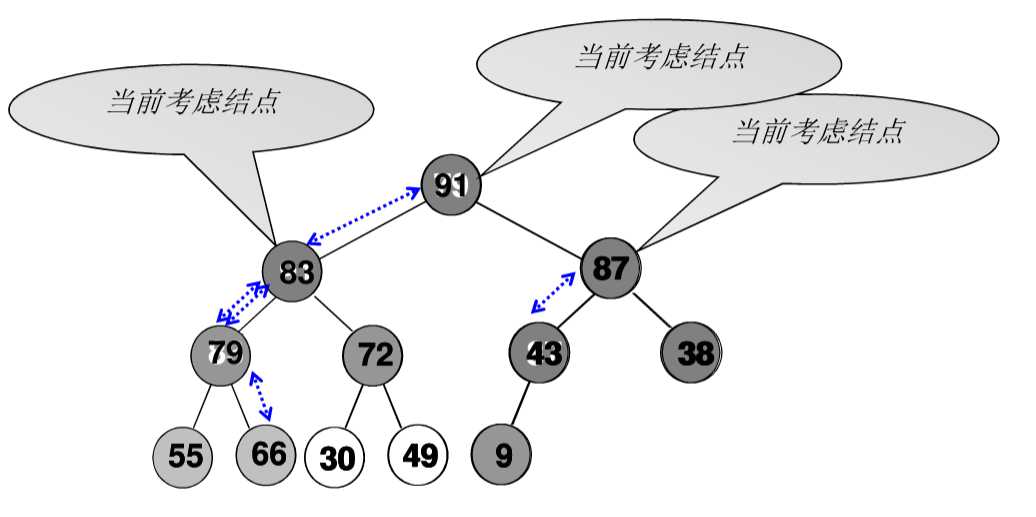
找出a现在的左右儿子中较大的那个

如果a比左右儿子中较大的那个要小

互换位置

继续比较a与左右儿子中较大的那个

直到a比左右儿子都要大

4、最大堆的建立：将N个元素按最大堆的要求存储在一维数组中

方法1：一个一个插入，效率较低

方法2：在线性时间复杂度下建立最大堆

　　　　（1）将N个元素按输入顺序存入，先满足完全二叉树的结构特性

　　　　（2）调整各结点位置，以满足最大堆的有序性

               

一个结点，左子树是一个最大堆，右子树是一个最大堆

从删除操作，我们已经知道如何将他们三者调成一个最大堆

那么现在我们可以倒过来，逐步建立最大堆

下图中，p表示结点——左子树——右子树模型中结点的下标

H表示完全二叉树，一开始不是最大堆，但执行完PerDown后是最大堆