挑战程序设计——二分图判定

Posted 2022-07-01 e-mperor

题目详情

Description

给定一个具有 n 个顶点的图。要给图上每个顶点染色，并且使相邻顶点颜色不同。问是否能最多用2种颜色进行染色？

限制条件：

1<= n <=1000

Input

第一行输入图中结点个数

接下来每一行依次输入：每个结点相邻的结点的个数，相邻的每个结点的值 

Output

Yes 或 No

Sample Input

3
2 1 2
2 0 2
2 0 1

Sample Output

No

题解

#include<bits/stdc++.h>
using namespace std;
 
const int MAX_V=1e3+5;
//输入
vector<int> G[MAX_V]; //图 
int V; //顶点数 
int color[MAX_V]; //顶点 i的颜色（1 or -1）
 
//把顶点染成1或-1 
bool dfs(int v,int c)
    color[v] = c; //把顶点 v染成颜色 c
    for(int i=0; i<G[v].size(); i++) //G[v].size()是与第 i个顶点相邻的顶点的数目
        //如果相邻顶点同色，返回 false
        if(color[G[v][i]] == c) return false;
        //如果相邻顶点未被染色，则染成 -c
        if(color[G[v][i]] == 0 && !dfs(G[v][i],-c)) return false;
    
    //如果所有顶点都被染色，返回 true
    return true;

void solve()
    for(int i=0; i<V; i++)
        if(color[i] == 0)
            //若顶点 i 未被染色，则染成 1
            if(!dfs(i,1))
                printf("No\\n");
                return;
            
        
    
    printf("Yes\\n");

 
int main(void)
    scanf("%d",&V);
    int count,vm;
    for(int i=0; i<V; i++)
        scanf("%d",&count); //该顶点相邻的顶点数
        for(int j=0; j<count; j++) //输入与第 i个结点相邻的各结点的数值 
            scanf("%d",&vm);
            G[i].push_back(vm);
        
        
    
    solve();
    return 0;

 
//4 //图中结点总数 
//2 1 3 //第一个数是该结点相邻的结点的个数，后两个数是相邻结点的值
//2 0 2
//2 1 3
//2 0 2
 
//Yes

 

把相邻顶点染成不同颜色的问题叫图着色问题。对图进行染色所需要的最小颜色数称为最小着色数。最小着色数是2的图称为二分图

如果只用2种颜色，确定一个顶点的颜色后，和它相邻的顶点的颜色也就确定。选择任意一个顶点出发，依次确定相邻顶点的颜色，就可以判断是否可以被2种颜色染色

可用深度搜索实现

如果是连通图，一次 dfs 就可以访问到所有的顶点。如果图不连通，需要依次检查每个顶点是否访问过，只需将 dfs 进行一些修改即可

---

图的种类

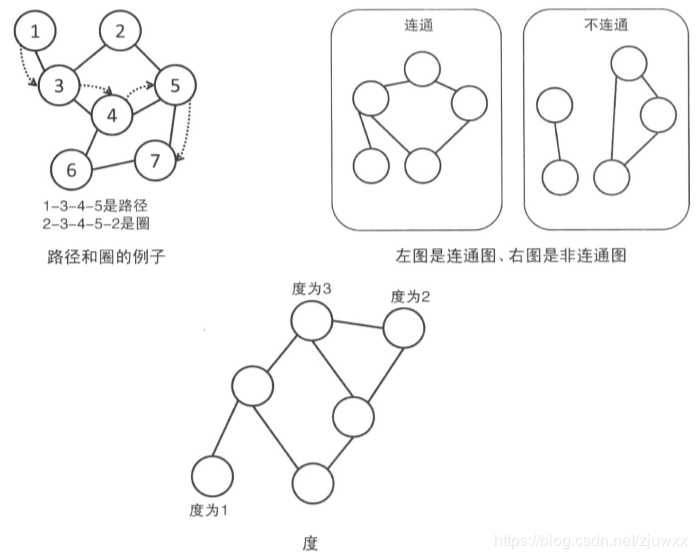
顶点的集合是V(vertex)、边的集合是E(edge)的图记为 G=(V, E)，连接两点u和v的边用 e=(u, v) 表示

1、无向图

顶点的边数叫这个顶点的度

相邻顶点的序列称为路径。起点和终点重合的路径称为圈

任意两点之间都有路径连接的图叫连通图。没有圈的连通图叫树（边数等于顶点数-1的连通图）。没有圈的非连通图叫森林

2、有向图

以有向图的顶点 v为起点的边的集合，其元素数目叫 v的出度。以顶点 v为终点的边的集合，其元素数目叫 v的入度

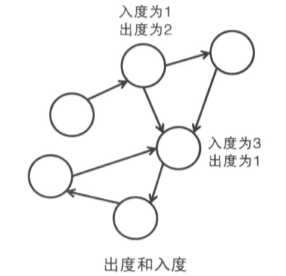
没有圈的有向图叫 DAG。在 DAG中给每个顶点一个编号，第 i 号顶点叫 vi。那么存在从顶点 vi 到顶点 vj 的边时就有 i < j 成立，这种编号方式叫拓扑序

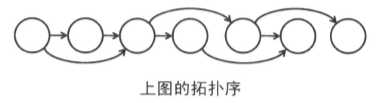
如果把图中的顶点按照拓扑序从左到右排序，那么所有的边都是从左指向右的。这样，有些 DAG问题就可以使用 DP解决

图的表示

记顶点和边的集合为 V和 E，|V|和 |E|表示顶点和边的数目。另外在 V中，顶点被编号为0~|V|-1

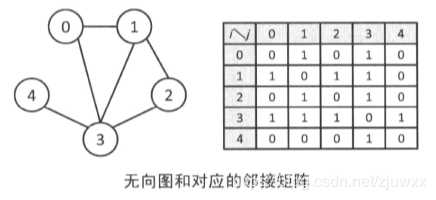
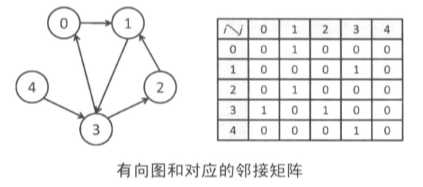
1、邻接矩阵

无向图中，如果顶点 i 和顶点 j 之间有边相连，那么 g[ i ][ j ] 和 g[ j ][ i ] 就设为1，否则设为0

 

有向图中，如果顶点 i 有一条指向顶点 j 的边，那么 g[ i ][ j ] 就设为1，否则设为0.不需要满足 g[ i ][ j ] =  g[ j ][ i ]

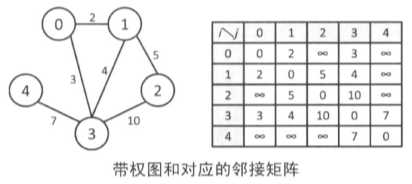
带权图中，g[ i ][ j ] 表示的是顶点 i 到顶点 j 的边的权值。在边不存在的情况下，令 g[ i ][ j ] 等于适当的较大的常数 INF

无向带权图仍要保持 g[ i ][ j ] =  g[ j ][ i ]

一条边上有多种不同权值时使用结构体或类作为数组的元素即可和原来一样对图进行处理

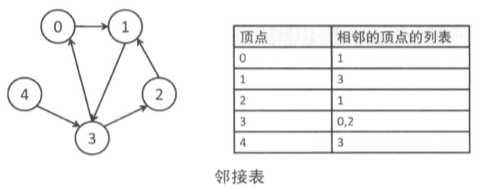
2、邻接表

用邻接矩阵表示稀疏图会浪费大量内存空间，用邻接表表示则可以大大节约，只需要 O( |V| + |E| ) 的内存空间

在带权图等边有附加属性的图中，将边用结构体或者类来表示即可方便的存储

在邻接表中查询两点间是否有边需要遍历一遍链表才能知道

数据输入：

3 3（顶点数 边数）
0 1（有一条0到1的边）
0 2（有一条0到2的边）
1 2（有一条1到2的边）

代码实现：

#include<bits/stdc++.h>
int V,E; //顶点，边 
const int MAX_V=1e3+50;
 
//样例一 
vector<int> G[MAX_V];
/*
 *边上有属性的情况
 *struct edge int to,cost; ;
 *vector<edge> G[MAX_V];
 */
 
int main()
    scanf("%d%d",&V,&E);
    for(int i=0;i<E;++i)
        //从 s向 t连边
        int s,t;
        scanf("%d%d",&s,&t);
        G[s].push_back(t);
        //如果是无向图，还需要再从 t向 s连边 
     
    /*
     *图的操作
     */
    return 0;

 
//样例二
struct vertex
    vertor<vertex*> edge;
    /*
     *顶点的属性 
     */
;
vertex G[MAX_V];
 
int main()
    scanf("%d%d",&V,&E);
    for(int i=0;i<E;++i)
        int s,t;
        scanf("%d%d",&s,&t);
        G[s].edge.push_back(&G[t]);
        //G[t].edge.push_back(&G[s]);
     
    /*
     *图的操作
     */
    return 0;