路径诱导系统
Posted
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了路径诱导系统相关的知识，希望对你有一定的参考价值。
要解决交通流的诱导问题就必须解决动态和随机的交通流量或平均车速在路段和交叉路口的分配问题，即“实时动态交通分配”。这一理论的主要功能是：预测交通运输系统状况、提供道路引导系统、引导车辆在最佳线路上行驶、为出行者提供出发时间和选择方式、提供诱导系统与交通控制系统的相互联系、为先进的交通管理系统和先进的交通信息系统提供了重要的理论基础。
为了有效的解决这一理论问题，需要运用交通规划相关理论，设计实际最优和预测最优动态交通分配算法。该模型的输入数据既是需要实施交通诱导区域内路网中各路段和路口的交通状态数据，建立目的地最优旅行线路的规划算法，最后产生诱导发布信息。诱导信息的构成将是当前最佳路径的引导。
下面简单介绍诱导系统及诱导算法。
1、智能交通系统（ITS）
意义：解决城市交通问题的最佳途径
关键技术基础：将信息、通信和计算机网络等技术有效地综合运用于地面交通管理体系，从而建立一种大范围、全方位的实时、准确、高效的交通管理系统。
主要功能：为道路使用者提供实时路况数据、道路图像信息、旅行时间服务、动态导航等服务，使公众出行更加便利，降低交通事故的发生率，缓解交通拥堵。
主要手段：
①车辆诱导系统：均衡道路网络交通负载的有效手段；
②城市交通信号控制：提高通行能力的重要手段。
本次主要对车辆诱导系统进行研究。
2、车辆诱导系统研究现状
2.1、美国TravTek系统
主要信息源：交叉口线圈、视频检测器。
通信模块：电话线路、调频广播、自动拨号蜂窝电话。
路径计算模块：车内定位计算机和路径优化计算机。
能根据用户的需求，从数据库中检索出当地的旅馆、饭店、加油站、停车场等服务信息，并制定最优路径。
属于分布式动态诱导系统，对车内的设施和信息传输技术要求较高，造价相对昂贵。
2.2德国Ali-Scout系统
主要信息源：磁场感应器、行程时间测量仪。
通信模块：道口两旁红外信标双向通信。
路径计算模块：车外路径诱导计算机。
属于中心式动态诱导系统，对交通信息处理中心要求较高。
2.3日本VICS系统
主要信息源：交通流检测器。
通信模块：无线电信标（高速公路）、红外信标（主干道）、FM多路广播；
属于中心式动态诱导系统。
日本VICS系统框架
3、车辆诱导系统的技术
3.1 常见车辆诱导系统结构
3.2 常用路径优化算法分析
常用路径优化算法分析
出行者对路径选择的要求会有所不同，根据不同的最优目标，定义相应的道路权重，反映到网络图上。
具体有以下几种方法：
①出行距离最短作为最优目标；
②出行时间最短；
③出行费用最小
④广义费用最小，是以目标中某两个或更多个的线性组合。
如
也可以采用CONTRAM费用方程:
,
其中C为出行费用，L:路段长度，T:出行时间，V：速度，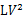
：耗油量，S：停车次数，D:延误，P：价格，R:危险程度，M：边际费用。
路径优化算法
①最短路径问题的经典算法
Dijkstra算法是典型最短路径算法, 是一种按路径长度递增的顺序产生最短路径的方法，能得出最短路径的最优解, 但由于它遍历计算的结点很多, 所以效率低。之后出现的Floyd算法在实际中搜索效率要好于Dijkstra算法，而Bellman算法虽然在时间复杂度方面由于Dijkstra算法，但实际效果往往不如Dijkstra算法。
A*算法是一种基于Dijkstra算法的启发式搜索算法，是目前广为流行的路径规划启发式算法, 它是一种最佳优先搜索算法, 对实现道路网的最佳优先搜索十分有用。启发式算法思想是引入启发式信息来提高搜索的效率，启发式信息有助于确定哪个结点最有希望成为后继结点并进行剪枝。
当以出行距离最短等静态网络作为路径优化目标时，可以直接使用Dijkstra算法或者A*算法。
idea：路段的权值也可以设计一个包含长度、交通环境以及时间段的函数。但依然是静态交通网络。
②基于时间依赖的动态交通网络最优路径算法
上面的算法都假设路段权值固定的静态网络，是以路径的空间距离作为优化目标。而在实际交通中，出行者往往关注的是关于时间费用，而不是空间距离，即网络中路段权值是依赖于时间的变量，属于动态交通网络。直接利用上述算法将出现错误。
图中结点a到d的最小路径为(a,b,c,d)=20，传统的Dijkstra算法结果是(a,c,d)=25。
因此我们的算法应该重点关注基于时间依赖网络的最优路径规划。
（1）目前主要的基于时间依赖的交通网络的最优路径算法，基本上采用这样的策略：首先使用Dijkstra或者A*算法根据当前估算的各路段行程时间计算一条从当前点到目标点的最优路径，以后每到一个路口结点，如果发现即将要通过的道路权重发生了较大改变，则根据当前路网各路段权重重新计算一条从当前点到目标点的最优路径。
这种方法所得一条路径实际上并不能保证是一条在动态路况中行程时间最少的路径。举个例子说明:假设当天道路的权重随时间变化的序列己经知道(实际上对将来发生的事情只能预测)，如图
在t1时刻车辆到达A，采用Dijkstra算法选择ABD这条路线到达目的地D，行驶了5分钟到B的时候，四条路段的权重都有了更新，BD从2变为4, CD还是保持3，继续行驶了4分钟到达D。实际上走ABD路径使用了9分钟，而走ACD只用8分钟。
《基于android的车载智能导航系统的研究与设计》夏国平 《一种基于实时路况信息的动态路径规划算法》雷东升
（2）基于时间预测的最优路径算法
算法的核心思想是，使用K条最短路径算法从静态权重的路网中选择K条备选路径，
然后根据路网中各路段行程时间的变化序列从这K条路径里面选出行程时间最少的路径。具体算法暂不在此叙述。
该算法需要知道一天的各路段行程时间序列，己经出现过的历史行程时间序列是可以确定的，应用算法可以得到实际的行程最少时间路径，但是实际应用需要知道当天的
行程时间序列，只能通过预测的方法得到，此时应用算法得到的路径是基于行程时间预测序列的行程时间最少路径，虽然不一定是实际行程时间最少的路径，但却可以随着预测精度的提高不断接近时间最少的最优路径。
该算法选择的路径也是一条十分接近实际行程时间最少的路径，完全可以满足实际的应用。但是算法的缺点是需要使用K最短路径算法，以及使用Dijkstra算法求出一个K条最短路径全程行驶时间的下界，下界如果不能起到过滤大量不可行路径的作用，还是需要在众多的路径中选择一条最优的路径，这会增加计算量，比普通的完全基于静态权重的求最优路径方法运算量要大，可行的改进方法是，针对使用最大权重计算得到的下界可能比较松的情形，需要对这个下界进一步收紧。具体改进方法不在此叙述。
《基于行程时间组合预测模型的动态路径诱导系统研究》陈悦
（3）一种时间最短路径算法
定理1为SPTDN算法的理论基础。
虽然能够在一定条件下求得最优解,但是由于其时间复杂度为(nmM2C),n是结点数，m是弧段数，M是时间段数，C是所有弧中最大的权值。当时间段数M比较大时，算法所用时间将比较大。
《时变_随机网络最优路径算法及其应用研究》谭国真
2、在SPTDN算法的基础上进行改进之后，算法有了更加广泛的适用范围。当城市实时导航系统给出的最小行程时间路径中某路段出现突发事件而被迫改变行进路线时，只要对当前位置进行相邻次数的计算，即可确定新的最小时间路径，极大地减少了路径搜索的次数。这样可以减少服务器的压力，这在城市实时导航系统中非常有用。所以改进后的最小时间路径算法更具实际应用价值。
改进后的最小时间路径算法已经成功应用于某市交警局中心系统中最短路径的搜索。该系统中以车牌自动识别系统的识别数据为源数据，通过相邻监测点间的识别数据比对来得到实测路段行程时间；用指数平滑法预测路段在未来若干个时间段内的行程时间。把行程时间作为时间段的一个函数，城市交通网络就抽象成了一个时间依赖的网络。
《车辆诱导系统及关键技术研究》翟晓峰
idea：在上述的改进算法中，用到了基于车牌自动识别系统的行程时间预测方法。如果能够结合已有的牌识实时算法库来获得各路段的预测行程时间，将极大地加快诱导算法的开发。
(4)其他算法
1、蚁群算法
将交通实时信息作为选择影响概率的一个因素—阻抗，应用于蚁群算法。将m只蚂蚁放到起点结点，迭代寻找最优路径，全部蚂蚁均将所有结点走过一遍。蚁群算法的准确性要高于Dijkstra算法，但蚁群算法则需要迭代上百次才能找出最优解,而且容易陷入局部最优,无法得到真正的最优路径，需要对传统蚁群算法进行改进。改进后的蚁群算法,在效率和准确性方面都远远超过前面的两种算法。
《基于实时交通信息的动态路径规划算法性能比较》黄西洲
改进的蚁群算法
给出一种在时变网络中蚁群算法的信息素更新策略, 使其能正确地反映边上权值的变化情况。针对传统蚁群算法收敛过早，容易陷入局部最优的问题，将蚁群算法与遗传算法相结合。
改进的算法在最优解概率和平均求解时间都得到明显提高，但是文中建立了40个结点的网络，只设置了8只蚂蚁参与运算。
参照其他资料，一般情况下，网络规模约为蚂蚁数目的1.5倍。蚂蚁数目的大小对运行时间的影响基本为线性相关。暂时难以估计实际中多结点的平均求解时间，有待于以后实验估计。
《改进蚁群算法求解时变网络中最短路径问题》刘永强
《交通网络路径选择及应用研究》陈京荣
2、遗传算法
①以一种随机Dijkstra算法为基础，运用遗传算法来求解动态网络最优路径。随机Dijkstra算法能够在不增加时间复杂度的基础上求解两点间最短路径问题，得出的路径适用于遗传算法初始种群的产生问题。
算法要比改进的Dijkstra算法在计算速度上快得多；同时由于遗传算法具有很强的鲁棒性，且初始种群的产生和交叉操作都是根据动态路径诱导最短路径问题(SPDRGS)而特别设计的，因此算法同时也具有很高的收敛效率, 能够在短时间内达到最优或较优解。
本文所采用的是广州市电子地图其中含有20000个结点、40000条路段、144个时间间隔。为了验证算法的有效性，本文在20000个结点中随机选取了50对OD，每对OD 进行了10 次计算。
《基于遗传算法的动态网络中最短路径问题算法》邹亮
《遗传算法在动态路径诱导系统中的应用》邹亮
②交互式遗传算法
与传统遗传算法相比，交互式遗传算法结合了人的偏好、直觉、情感和心理特征等主观因素。交互式遗传算法的优化结果更趋合理，更符合个体的需要。出行者可以根据自己的需要选择最佳的出行路径，这可以在一定程度上消除动态路径诱导中的Bracess现象，在一定程度上避免车辆选择相同的、以前并不拥挤的道路，使这条道路可能很快变得拥挤。
实验所用的数据是成都市区道路交通网络，此交通网络共有5427个结点，7978条边;共分260个时间间隔。随机选取了10对OD。每对OD选取不同的初始种群计算了3次，试验结果如表所示。
《基于GIS_T的城市交通最优路径诱导算法研究》张水舰
(5)多目标最优
利用k-最短路算法来获得双目标最短路的方法，获得多条有效路径,使得决策者可以对这些路径进行比较和选择。同时, 在求解的过程中,决策者可以根据获得有效路径的情况, 对各个目标的上限进行调整, 获得满足决策者要求的有效路径集合。
属于静态网络最优路径规划，只能用以出行距离最短等固定权值作为路径优化目标时。
《基于一种求解双目标最短路的方法》魏航
《双目标最短路有效解的快速算法》郝光
《多目标最短路径模型及算法》郝光
(6)考虑网络地理特征的改进思想
①层次型网络模型
近年来路径规划很多研究主要集中在对道路的预处理方法上，通过对道路网络的预处理来挖掘一些可以提高路径搜索效率的信息来优化路径计算的性能。其中的经验层级路网，是一种对道路网络做预处理的方法，这种预处理方法使路径规划的结果更加高效合理。思路是在预处理阶段建立一种经验的层级路网。首先，这里建立的层级路网，将路径计算中的道路优先级对应于路网的层级。层级性越高的道路在路径计算时其优先权越高。其次，这里的道路分层方法是基于一种经验方法，这种经验是从对于导航路径选择很熟悉的出租车司机的路径轨迹中挖掘出来的。采用这种经验来决定路径规划的道路网络层级性，也就是说在我们的经验层级路网中，层级性越高的应该就是经验上优先的道路。这样，在路径规划中我们就
可以采用高层道路优先的方法来高效地搜索出符合经验的“好”路径。
由于层次网络模型理论复杂，一般是在遇到现有算法无法满足复杂道路的情况下的最优路径规划时，用来提高路径搜索效率。
《面向导航路径选择的道路网络经验层级模型研究》曾喆
《时变_随机网络最优路径算法及其应用研究》谭国真
②限制搜索区域
针对椭圆限制搜索区域算法效率的不足，陆锋提出了基于椭圆的最小外接正矩形限制搜索区域的算法。矩形限制搜索区域算法的基础是椭圆限制搜索区域算法，椭圆算法中限制椭圆的长轴是采用统计分析方法完成的。具体方法暂不在此叙述。
《基于GIS的最优路径算法研究与实现》王海梅
日本VICS系统迅速发展的原因:
1、经过几十年的ITS建设，各种硬件和相关设施都比较完善；
2、日本各个相关部门有效的合作和积极推动；
3、VICS系统也在不断丰富信息内容提高信息的精确度；
4、良好的商业运作模式和市场化运作、积极推进国际标准、不断修正和完善。
与日本相比，目前我国的道路信息系统的不足：
1、道路交通信息采集体系还不够完善；
2、车载GPS终端种类繁多，车载信息服务标准化滞后， 车载信息服务还没有走向批量市场
3、各相关部门配合不够
基于此，对于车辆诱导系统的开发任务，应尽量利用较准确、稳定的交通信息采集方法，综合分析多种在实际应用中较为成熟的算法，包括数据融合、交通状态判别算法，最优路径算法等，以保证系统的准确性要求。
数据融合，在硬件设备不完善的前提下尽量获得足够多的交通信息，并进行有效处理，使得信息足够丰富和可靠。
交通状态判别，诱导系统可靠性的基础。
最优路径算法，系统核心，功能需求的多样化和用户个性化，算法的设计也应当丰富化。
以上是关于路径诱导系统的主要内容，如果未能解决你的问题，请参考以下文章
Knowledge Tracing -- 基于贝叶斯的学生知识点追踪（BKT）