Kalman FilterExtended Kalman Filter以及Unscented Kalman Filter介绍

Posted 2022-06-19 sunwq06

模型定义

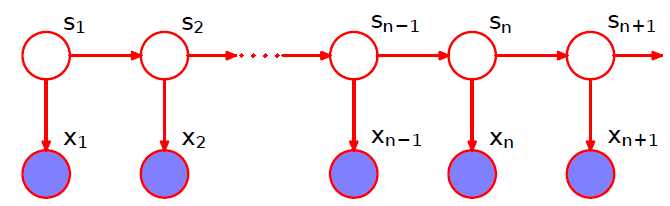
如上图所示，卡尔曼滤波(Kalman Filter)的基本模型和隐马尔可夫模型类似，不同的是隐马尔科夫模型考虑离散的状态空间，而卡尔曼滤波的状态空间以及观测空间都是连续的，并且都属于高斯分布，因此卡尔曼滤波又称为linear Gaussian Markov model，它的数学定义如下：$$\\underbraces_t=C s_t-1+G h_t+\\gamma_t_\\text latent process , \\quad \\underbracex_t=D s_t+\\varepsilon_t_\\text observed process $$其中$h_t$表示控制向量(control vector)，是已知量；$\\gamma_t \\sim N(0, Q)$表示状态误差，它包含了状态转换公式$C s_t-1+G h_t$中未考虑到的其它因素，是状态转换公式准确性的度量；$\\varepsilon_t \\sim N(0, V)$表示观测误差，是观测精度的度量。下面举一个简单的例子：

• 假设有一个二维空间上的物体位置的观测序列($x_t \\in \\mathbbR^2$)，观测有一定误差；该物体的状态$s_t=[p_t1,v_t1,p_t2,v_t2]^T$，其中$p_t$和$v_t$表示物体位置和速度，下标1和2表示方向；控制向量为$h_t=[a_t1,a_t2]^T$，$a_t$表示加速度。由基本的物理公式可知$$s_t=\\underbrace\\left[\\beginarraycccc1 & \\Delta t & 0 & 0 \\\\ 0 & 1 & 0 & 0 \\\\ 0 & 0 & 1 & \\Delta t \\\\ 0 & 0 & 0 & 1\\endarray\\right]_Cs_t-1+\\underbrace\\left[\\beginarraycc \\frac12(\\Delta t)^2 & 0 \\\\ \\Delta t & 0 \\\\ 0 & \\frac12(\\Delta t)^2 \\\\ 0 & \\Delta t\\endarray\\right]_Gh_t+\\gamma_t\\text 以及 x_t=\\underbrace\\left[\\beginarraycccc1 & 0 & 0 & 0 \\\\ 0 & 0 & 1 & 0\\endarray\\right]_Ds_t+\\varepsilon_t$$

卡尔曼滤波的目标是已知观测序列$x_1,x_2,\\cdots,x_t$，计算当前隐藏状态的分布函数，即$$s_t\\left|s_t-1 \\sim N\\left(C s_t-1+G h_t, Q\\right), \\quad x_t\\right| s_t \\sim N\\left(D s_t, V\\right)\\quad
\\Rightarrow\\quad p\\left(s_t | x_1, \\dots, x_t\\right);\\quad 1\\leq t \\leq T$$注意除观测序列以外，矩阵$C,G,Q,D,V$以及控制向量$h_t$也是给定的。 

模型求解

• 定义$S_t=(s_t | x_1, \\ldots, x_t)$，容易看出$S_t$满足高斯分布$N(\\mu_t, \\Sigma_t)$，$\\mu_t$以及$\\Sigma_t$即为需要求解的量
  • 为方便之后的计算，令$S_t-1=(s_t-1 | x_1, \\ldots, x_t-1)=\\underbrace\\mu_t-1_\\textmean+\\Delta S_t-1,\\quad \\Delta S_t-1 \\sim N(0,\\Sigma_t-1)$
• 定义$P_t= (s_t | x_1, \\ldots, x_t-1)$，有$P_t=CS_t-1+G h_t+\\gamma_t$
  • 为方便之后的计算，令$P_t=\\underbraceC\\mu_t-1+Gh_t_\\mu_P_t+\\underbraceC\\Delta S_t-1+\\gamma_t_\\Delta P_t$
• 定义$O_t= (x_t | x_1, \\ldots, x_t-1)$，有$O_t=DP_t+\\varepsilon_t$
  • 为方便之后的计算，令$O_t=\\underbraceD(C\\mu_t-1+Gh_t)_\\mu_O_t+\\underbraceDC\\Delta S_t-1+D\\gamma_t+\\varepsilon_t_\\Delta O_t$

由上述定义可知 $$\\left[\\beginarrayc P_t \\\\ O_t \\endarray\\right] \\sim N\\left(\\left[\\beginarrayc \\mu_P_t \\\\ \\mu_O_t \\endarray\\right], \\left[\\beginarraycc \\Sigma_PP & \\Sigma_PO\\\\ \\Sigma_PO^T & \\Sigma_OO \\endarray\\right] \\right)$$接下来计算协方差矩阵的这些项：

• $\\Sigma_PP=\\mathbbE[\\Delta P_t (\\Delta P_t)^T]=C\\mathbbE[\\Delta S_t-1 (\\Delta S_t-1)^T]C^T+\\mathbbE[\\gamma_t\\gamma_t^T]=C\\Sigma_t-1C^T+Q$
• $\\Sigma_PO=\\mathbbE[\\Delta P_t (\\Delta O_t)^T]=C\\mathbbE[\\Delta S_t-1 (\\Delta S_t-1)^T]C^TD^T+\\mathbbE[\\gamma_t\\gamma_t^T]D^T=C\\Sigma_t-1C^TD^T+QD^T$
• $\\Sigma_OO=\\mathbbE[\\Delta O_t (\\Delta O_t)^T]=DC\\mathbbE[\\Delta S_t-1 (\\Delta S_t-1)^T]C^TD^T+D\\mathbbE[\\gamma_t\\gamma_t^T]D^T+\\mathbbE[\\varepsilon_t\\varepsilon_t^T]=DC\\Sigma_t-1C^TD^T+DQD^T+V$

容易看出$S_t=(P_t | O_t)$，此外定义$$\\hat\\mu_t=\\mu_P_t=C \\mu_t-1+Gh_t，\\text  \\hat\\Sigma_t=\\Sigma_PP=C \\Sigma_t-1 C^T+Q\\text以及卡尔曼增益矩阵K_t=\\hat\\Sigma_tD^T[D\\hat\\Sigma_tD^T+V]^-1$$由高斯分布的性质可知

• $\\Sigma_t=\\Sigma_PP-\\Sigma_PO\\Sigma_OO^-1\\Sigma_PO^T=(I-K_tD)\\hat\\Sigma_t$
• $\\mu_t=\\mu_P_t+\\Sigma_PO\\Sigma_OO^-1(O_t-\\mu_O_t)=\\hat\\mu_t+K_t(x_t-D\\hat\\mu_t)$

上述求解过程可归纳为：

1. 初始化$\\mu_0$以及$\\Sigma_0$
2. 预测：$\\hat\\mu_t=C \\mu_t-1+Gh_t$以及$\\hat\\Sigma_t=C \\Sigma_t-1 C^T+Q$
3. 计算卡尔曼增益矩阵$K_t=\\hat\\Sigma_tD^T[D\\hat\\Sigma_tD^T+V]^-1$
4. 更新：$\\mu_t=\\hat\\mu_t+K_t(x_t-D\\hat\\mu_t)$以及$\\Sigma_t=(I-K_tD)\\hat\\Sigma_t$

Extended Kalman Filter

在Extended Kalman Filter中，状态之间的转化以及状态向观测的转化是非线性的，即$$s_t=g(s_t-1,h_t)+\\gamma_t,\\text  x_t=f(s_t)+\\varepsilon_t;\\text  其中g,f\\text代表非线性函数$$此时考虑使用泰勒公式将非线性函数近似为线性函数，延续上一部分的定义，有

• $P_t=g(S_t-1,h_t)+\\gamma_t=g(\\mu_t-1+\\delta S_t-1,h_t)+\\gamma_t=\\underbraceg(\\mu_t-1,h_t)_\\mu_P_t(\\texti.e., \\hat\\mu_t)+\\underbraceJ_g\\Delta S_t-1+\\gamma_t_\\Delta P_t$
• $O_t=h(P_t)+\\varepsilon_t=f(\\mu_P_t+\\Delta P_t)+\\varepsilon_t=f(\\mu_P_t)+J_f\\Delta P_t+\\varepsilon_t=\\underbracef(\\hat\\mu_t)_\\mu_O_t+\\underbraceJ_fJ_g\\Delta S_t-1+J_f\\gamma_t+\\varepsilon_t_\\Delta O_t$

其中$J_g$和$J_f$为Jacobian矩阵，假设状态为$m$维向量，观测为$n$维向量，并且$g(s,h)=[g_1(s,h),\\cdots,g_m(s,h)]^T$以及$f(s)=[f_1(s),\\cdots,f_n(s)]^T$，则有$$J_g=\\left[\\beginarraycccc\\frac\\partial g_1\\partial \\mu_t-1,1 & \\frac\\partial \\mu_1\\partial s_t-1,2 & \\cdots & \\frac\\partial g_1\\partial \\mu_t-1,m \\\\ \\vdots & \\vdots & \\vdots & \\vdots \\\\ \\frac\\partial g_m\\partial \\mu_t-1,1 & \\frac\\partial g_m\\partial \\mu_t-1,2 & \\cdots & \\frac\\partial g_m\\partial \\mu_t-1,m\\endarray\\right], \\text   J_f=\\left[\\beginarraycccc\\frac\\partial f_1\\partial \\hat\\mu_t,1 & \\frac\\partial f_1\\partial \\hat\\mu_t,2 & \\cdots & \\frac\\partial f_1\\partial \\hat\\mu_t,m \\\\ \\vdots & \\vdots & \\vdots & \\vdots \\\\ \\frac\\partial f_n\\partial \\hat\\mu_t,1 & \\frac\\partial f_n\\partial \\hat\\mu_t,2 & \\cdots & \\frac\\partial f_n\\partial \\hat\\mu_t,m\\endarray\\right]$$容易看出Extended Kalman Filter的求解过程可归纳为：

1. 初始化$\\mu_0$以及$\\Sigma_0$
2. 预测：$\\hat\\mu_t=g(\\mu_t-1,h_t)$以及$\\hat\\Sigma_t=J_g \\Sigma_t-1 J_g^T+Q$
3. 计算卡尔曼增益矩阵$K_t=\\hat\\Sigma_tJ_f^T[J_f\\hat\\Sigma_tJ_f^T+V]^-1$
4. 更新：$\\mu_t=\\hat\\mu_t+K_t[x_t-f(\\hat\\mu_t)]$以及$\\Sigma_t=(I-K_tJ_f)\\hat\\Sigma_t$

Unscented Kalman Filter

Unscented Kalman Filter和Extended Kalman Filter的模型定义一样，只是具体求解方法不同。相对于Extended Kalman Filter使用泰勒公式近似非线性函数，Unscented Kalman Filter通过选取多个样本点(the sigma points)直接估计均值和方差。仍然延续之前的定义，假设状态为$m$维向量，从随机变量$S_t-1$中选取$2m+1$个样本点，记为矩阵$\\mathcalX_t-1$($m$行$2m+1$列)，选取方式为$$\\mathcalX_t-1=\\left[\\beginarrayccc\\mu_t-1 & \\mu_t-1+\\sqrt(m+\\lambda )\\Sigma_t-1 & \\mu_t-1-\\sqrt(m+\\lambda )\\Sigma_t-1 \\endarray\\right]$$若将$\\Sigma_t-1$进行Cholesky分解得到$LL^T$，则$\\sqrt\\Sigma_t-1=L$；或者对$\\Sigma_t-1$进行特征值分解得到$U\\Lambda U^T$(其中$\\Lambda$为对角阵)，则$\\sqrt\\Sigma_t-1=U\\Lambda^1/2$。接下来对每个采样点分配权重：

• $\\vecw_a=\\left[\\beginarrayccccc\\frac\\lambdam+\\lambda & \\frac12(m+\\lambda) & \\frac12(m+\\lambda) & \\cdots & \\frac12(m+\\lambda)\\endarray\\right]$
• $\\vecw_c=\\left[\\beginarrayccccc\\frac\\lambdam+\\lambda+(1-\\alpha^2+\\beta) & \\frac12(m+\\lambda) & \\frac12(m+\\lambda) & \\cdots & \\frac12(m+\\lambda)\\endarray\\right]$

其中$\\vecw_a$为求均值时的权重，$\\vecw_c$为求协方差矩阵时的权重。针对一些参数的取值有以下建议：$$\\alpha \\in (0,1],\\text  \\beta=2,\\text  \\lambda=\\alpha^2(m+\\kappa)-m,\\text  \\kappa\\geq 0$$将$\\mathcalX_t-1$代入函数$g$可以得到$$\\hat\\mathcalX_t=\\left[\\beginarrayccccg(\\mathcalX_t-1^[1],h_t) & g(\\mathcalX_t-1^[2],h_t)  & \\cdots & g(\\mathcalX_t-1^[2m+1],h_t)\\endarray\\right]$$其中上标表示矩阵的列数，由$\\hat\\mathcalX_t$可以估计出$\\hat\\mu_t$以及$\\hat\\Sigma_t$，接下来可以通过两种方式得到观测的采样点$\\mathcalZ_t$：

1. 直接通过$\\hat\\mathcalX_t$进行计算，即$$\\mathcalZ_t=\\left[\\beginarraycccch(\\hat\\mathcalX_t^[1]) & h(\\hat\\mathcalX_t^[2])  & \\cdots & h(\\hat\\mathcalX_t^[2m+1]) \\endarray\\right]$$
2. 通过得到的$\\hat\\mu_t$以及$\\hat\\Sigma_t$重新采样，有公式$$\\hat\\mathcalX_t^*=\\left[\\beginarrayccc\\hat\\mu_t & \\hat\\mu_t+\\sqrt(m+\\lambda )\\hat\\Sigma_t & \\hat\\mu_t-\\sqrt(m+\\lambda )\\hat\\Sigma_t \\endarray\\right]$$然后计算过程同第一种方式，即$$\\mathcalZ_t=\\left[\\beginarraycccch(\\hat\\mathcalX_t^*[1]) & h(\\hat\\mathcalX_t^*[2])  & \\cdots & h(\\hat\\mathcalX_t^*[2m+1]) \\endarray\\right]$$

最后估计观测的均值和协方差矩阵，进而得到最终的结果，Unscented Kalman Filter的求解过程可归纳为：

1. 初始化$\\mu_0$以及$\\Sigma_0$
2. 预测：$\\hat\\mu_t=\\sum_j=1^2m+1w_aj\\hat\\mathcalX_t^[j]$以及$\\hat\\Sigma_t=\\sum_j=1^2m+1w_cj(\\hat\\mathcalX_t^[j]-\\hat\\mu_t)(\\hat\\mathcalX_t^[j]-\\hat\\mu_t)^T+Q$
3. 计算$\\mathcalZ_t$（从上述两种方式中选择一种），得到$\\mu_O_t=\\sum_j=1^2m+1w_aj\\mathcalZ_t^[j]$以及$\\Sigma_OO=\\sum_j=1^2m+1w_cj(\\mathcalZ_t^[j]-\\mu_O_t)(\\mathcalZ_t^[j]-\\mu_O_t)^T+V$
4. 计算$\\Sigma_PO=\\sum_j=1^2m+1w_cj(\\hat\\mathcalX_t^[j]-\\hat\\mu_t)(\\mathcalZ_t^[j]-\\mu_O_t)^T$，注意若使用第二种方式计算$\\mathcalZ_t$，需将公式中的$\\hat\\mathcalX_t$替换为$\\hat\\mathcalX_t^*$
5. 计算卡尔曼增益矩阵$K_t=\\Sigma_PO\\Sigma_OO^-1$
6. 更新：$\\mu_t=\\hat\\mu_t+K_t[x_t-\\mu_O_t]$以及$\\Sigma_t=\\hat\\Sigma_t-\\Sigma_PO\\Sigma_OO^-1\\Sigma_PO^T=\\hat\\Sigma_t-K_t\\Sigma_OOK_t^T$