hourglassnet网络解析

Posted 2022-06-19 yongjieshi

hourglassnet中文名称是沙漏网络，起初用于人体关键点检测，代码，https://github.com/bearpaw/pytorch-pose

后来被广泛的应用到其他领域，我知道的有双目深度估计，关于双目深度估计，自己最近会写一篇blog，这里先简单介绍一下。双目深度估计第一次用hourglassnet是在psmnet（https://github.com/JiaRenChang/PSMNet）中使用的的，后来的很多双目深度估计的工作也有很多继承这种hourglass的使用方法，比如gwcnet（https://github.com/xy-guo/GwcNet）

在这里就详细解说一下hourglassnet的网络结构，hourglassnet作者已经公开了代码，这里参考这个代码：https://github.com/bearpaw/pytorch-pose/blob/master/pose/models/hourglass.py

代码如下

import torch.nn as nn
import torch.nn.functional as F
from tensorboardX import SummaryWriter
# from .preresnet import BasicBlock, Bottleneck
import torch
from torch.autograd import Variable

class Bottleneck(nn.Module):
    expansion = 2

    def __init__(self, inplanes, planes, stride=1, downsample=None):
        super(Bottleneck, self).__init__()

        self.bn1 = nn.BatchNorm2d(inplanes)
        self.conv1 = nn.Conv2d(inplanes, planes, kernel_size=1, bias=True)
        self.bn2 = nn.BatchNorm2d(planes)
        self.conv2 = nn.Conv2d(planes, planes, kernel_size=3, stride=stride,
                               padding=1, bias=True)
        self.bn3 = nn.BatchNorm2d(planes)
        self.conv3 = nn.Conv2d(planes, planes * 2, kernel_size=1, bias=True)
        self.relu = nn.ReLU(inplace=True)
        self.downsample = downsample
        self.stride = stride

    def forward(self, x):
        residual = x

        out = self.bn1(x)
        out = self.relu(out)
        out = self.conv1(out)

        out = self.bn2(out)
        out = self.relu(out)
        out = self.conv2(out)

        out = self.bn3(out)
        out = self.relu(out)
        out = self.conv3(out)

        if self.downsample is not None:
            residual = self.downsample(x)

        out += residual

        return out

# houglass实际上是一个大的auto encoder
class Hourglass(nn.Module):
    def __init__(self, block, num_blocks, planes, depth):
        super(Hourglass, self).__init__()
        self.depth = depth
        self.block = block
        self.hg = self._make_hour_glass(block, num_blocks, planes, depth)

    def _make_residual(self, block, num_blocks, planes):
        layers = []
        for i in range(0, num_blocks):
            layers.append(block(planes*block.expansion, planes))
        return nn.Sequential(*layers)

    def _make_hour_glass(self, block, num_blocks, planes, depth):
        hg = []
        for i in range(depth):
            res = []
            for j in range(3):
                res.append(self._make_residual(block, num_blocks, planes))
            if i == 0:
                res.append(self._make_residual(block, num_blocks, planes))
            hg.append(nn.ModuleList(res))
        return nn.ModuleList(hg)

    def _hour_glass_forward(self, n, x):
        up1 = self.hg[n-1][0](x)
        low1 = F.max_pool2d(x, 2, stride=2)
        low1 = self.hg[n-1][1](low1)

        if n > 1:
            low2 = self._hour_glass_forward(n-1, low1)
        else:
            low2 = self.hg[n-1][3](low1)
        low3 = self.hg[n-1][2](low2)
        up2 = F.interpolate(low3, scale_factor=2)
        out = up1 + up2
        return out

    def forward(self, x):
        return self._hour_glass_forward(self.depth, x)


class HourglassNet(nn.Module):
    ‘‘‘Hourglass model from Newell et al ECCV 2016‘‘‘
    def __init__(self, block, num_stacks=2, num_blocks=4, num_classes=16):
        super(HourglassNet, self).__init__()

        self.inplanes = 64
        self.num_feats = 128
        self.num_stacks = num_stacks
        self.conv1 = nn.Conv2d(3, self.inplanes, kernel_size=7, stride=2, padding=3,
                               bias=True)
        self.bn1 = nn.BatchNorm2d(self.inplanes)
        self.relu = nn.ReLU(inplace=True)
        self.layer1 = self._make_residual(block, self.inplanes, 1)
        self.layer2 = self._make_residual(block, self.inplanes, 1)
        self.layer3 = self._make_residual(block, self.num_feats, 1)
        self.maxpool = nn.MaxPool2d(2, stride=2)

        # build hourglass modules
        ch = self.num_feats*block.expansion
        hg, res, fc, score, fc_, score_ = [], [], [], [], [], []
        for i in range(num_stacks):
            hg.append(Hourglass(block, num_blocks, self.num_feats, 4))
            res.append(self._make_residual(block, self.num_feats, num_blocks))
            fc.append(self._make_fc(ch, ch))
            score.append(nn.Conv2d(ch, num_classes, kernel_size=1, bias=True))
            if i < num_stacks-1:
                fc_.append(nn.Conv2d(ch, ch, kernel_size=1, bias=True))
                score_.append(nn.Conv2d(num_classes, ch, kernel_size=1, bias=True))
        self.hg = nn.ModuleList(hg)
        self.res = nn.ModuleList(res)
        self.fc = nn.ModuleList(fc)
        self.score = nn.ModuleList(score)
        self.fc_ = nn.ModuleList(fc_)
        self.score_ = nn.ModuleList(score_)

    def _make_residual(self, block, planes, blocks, stride=1):
        downsample = None
        if stride != 1 or self.inplanes != planes * block.expansion:
            downsample = nn.Sequential(
                nn.Conv2d(self.inplanes, planes * block.expansion,
                          kernel_size=1, stride=stride, bias=True),
            )

        layers = []
        layers.append(block(self.inplanes, planes, stride, downsample))
        self.inplanes = planes * block.expansion
        for i in range(1, blocks):
            layers.append(block(self.inplanes, planes))

        return nn.Sequential(*layers)

    def _make_fc(self, inplanes, outplanes):
        bn = nn.BatchNorm2d(inplanes)
        conv = nn.Conv2d(inplanes, outplanes, kernel_size=1, bias=True)
        return nn.Sequential(
                conv,
                bn,
                self.relu,
            )

    def forward(self, x):
        out = []
        x = self.conv1(x)
        x = self.bn1(x)
        x = self.relu(x)

        x = self.layer1(x)
        x = self.maxpool(x)
        x = self.layer2(x)
        x = self.layer3(x)

        for i in range(self.num_stacks):
            y = self.hg[i](x)
            y = self.res[i](y)
            y = self.fc[i](y)
            score = self.score[i](y)
            out.append(score)
            if i < self.num_stacks-1:
                fc_ = self.fc_[i](y)
                score_ = self.score_[i](score)
                x = x + fc_ + score_

        return out


if __name__ == "__main__":
    model = HourglassNet(Bottleneck, num_stacks=2, num_blocks=4, num_classes=2)
    model2 = Hourglass(block=Bottleneck, num_blocks=4, planes=128, depth=4)
    input_data = Variable(torch.rand(2, 3, 256, 256))
    input_data2 = Variable(torch.rand(2, 256, 64, 64))
    
    output = model(input_data)
    print(output)
    # writer = SummaryWriter(log_dir=‘../log‘, comment=‘source_arc‘)
    # with writer:
    #     writer.add_graph(model2, (input_data2, ))

View Code

这里一步一步讲

以往的auto-ecoder最小的单元可能是一个卷积层，这里作者最小的单元是一个Bottleneck

作者先写了hourglss这个module，hourglass具体的网络结构如下，图片有点儿大，可以右键在新窗口中打开高清图片

 

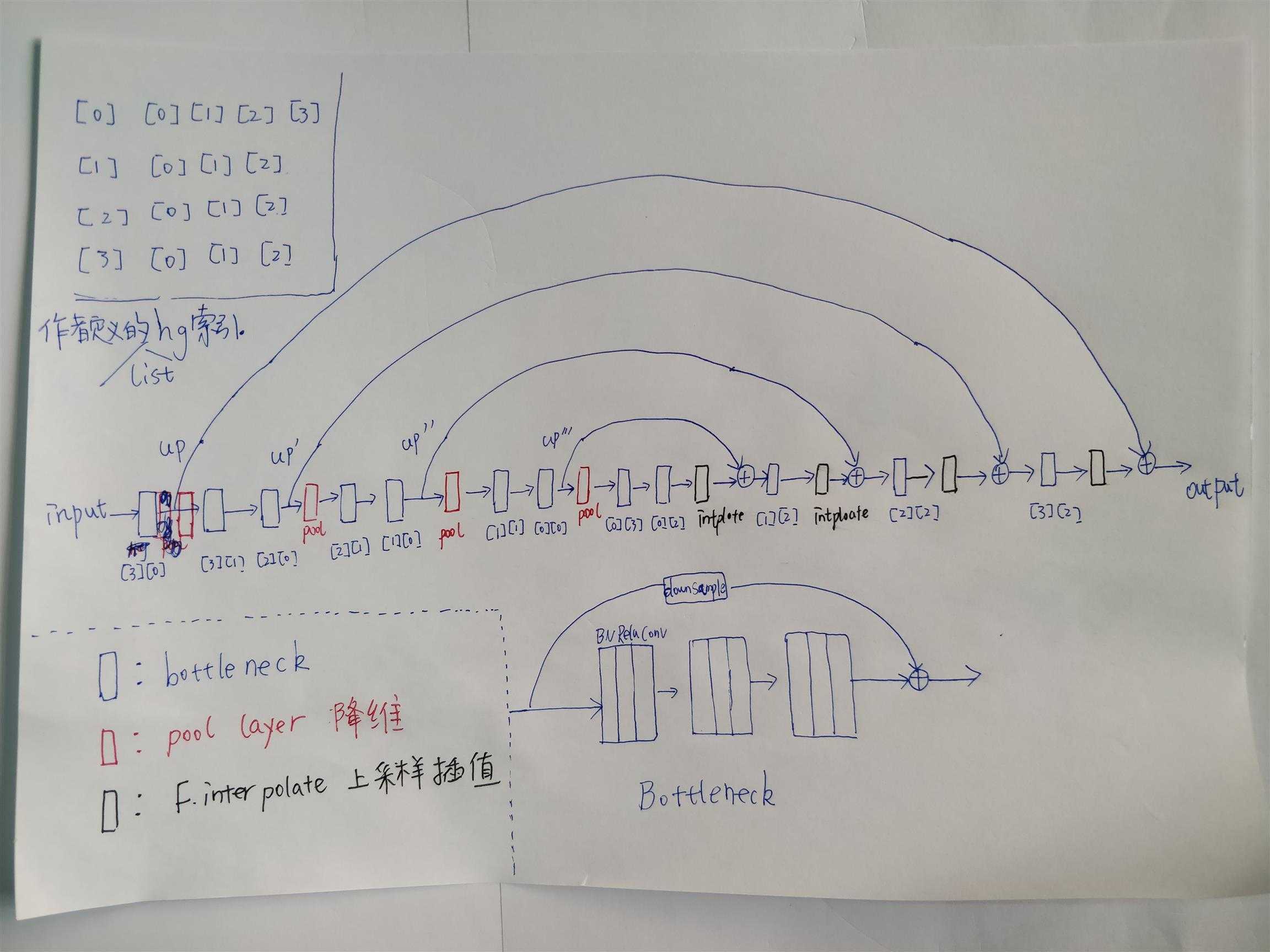
为了区分我还是说明一下几个概念，

bottleneck构成hourglass模块

hourglass模块以及其他模块构成最后的hourglass net

bottle模块代码如下

class Bottleneck(nn.Module):
    expansion = 2

    def __init__(self, inplanes, planes, stride=1, downsample=None):
        super(Bottleneck, self).__init__()

        self.bn1 = nn.BatchNorm2d(inplanes)
        self.conv1 = nn.Conv2d(inplanes, planes, kernel_size=1, bias=True)
        self.bn2 = nn.BatchNorm2d(planes)
        self.conv2 = nn.Conv2d(planes, planes, kernel_size=3, stride=stride,
                               padding=1, bias=True)
        self.bn3 = nn.BatchNorm2d(planes)
        self.conv3 = nn.Conv2d(planes, planes * 2, kernel_size=1, bias=True)
        self.relu = nn.ReLU(inplace=True)
        self.downsample = downsample
        self.stride = stride

    def forward(self, x):
        residual = x

        out = self.bn1(x)
        out = self.relu(out)
        out = self.conv1(out)

        out = self.bn2(out)
        out = self.relu(out)
        out = self.conv2(out)

        out = self.bn3(out)
        out = self.relu(out)
        out = self.conv3(out)

        if self.downsample is not None:
            residual = self.downsample(x)

        out += residual

        return out

View Code

hourglass模块代码如下

# houglass实际上是一个大的auto encoder
class Hourglass(nn.Module):
    def __init__(self, block, num_blocks, planes, depth):
        super(Hourglass, self).__init__()
        self.depth = depth
        self.block = block
        self.hg = self._make_hour_glass(block, num_blocks, planes, depth)

    def _make_residual(self, block, num_blocks, planes):
        layers = []
        for i in range(0, num_blocks):
            layers.append(block(planes*block.expansion, planes))
        return nn.Sequential(*layers)

    def _make_hour_glass(self, block, num_blocks, planes, depth):
        hg = []
        for i in range(depth):
            res = []
            for j in range(3):
                res.append(self._make_residual(block, num_blocks, planes))
            if i == 0:
                res.append(self._make_residual(block, num_blocks, planes))
            hg.append(nn.ModuleList(res))
        return nn.ModuleList(hg)

    def _hour_glass_forward(self, n, x):
        up1 = self.hg[n-1][0](x)
        low1 = F.max_pool2d(x, 2, stride=2)
        low1 = self.hg[n-1][1](low1)

        if n > 1:
            low2 = self._hour_glass_forward(n-1, low1)
        else:
            low2 = self.hg[n-1][3](low1)
        low3 = self.hg[n-1][2](low2)
        up2 = F.interpolate(low3, scale_factor=2)
        out = up1 + up2
        return out

    def forward(self, x):
        return self._hour_glass_forward(self.depth, x)

View Code

不仅仅是这里用到了bottleneck模块，后面的整体网络中也用到了此模块

如上图，bottleneck这个模块作为一个基本的单元构成了hourglass模块，可以看出网络还是挺庞大的，中间用pool进行降维，之后用F.interpolate函数进行升维，F.interpolate有一个参数是缩放多少倍，代替了反卷积复杂的步骤，直接进行成倍缩放。关于这个函数和反卷积之间的区别，我也不是特别理解

这样就基本上构成了一个大的auto-encoder，传统意义上来说，比如说分割，或者是其他的dense prediction的任务，到这里就结束了，因为一个auto-encoder就能够解决问题，但是作者不这样做，作者把这个架构作为一个基本的单元进行叠加，还可以重复很多这样的单元来提高精度，显然显存是一个很大的瓶颈，所以作者在实验的时候只叠了两层，见下图

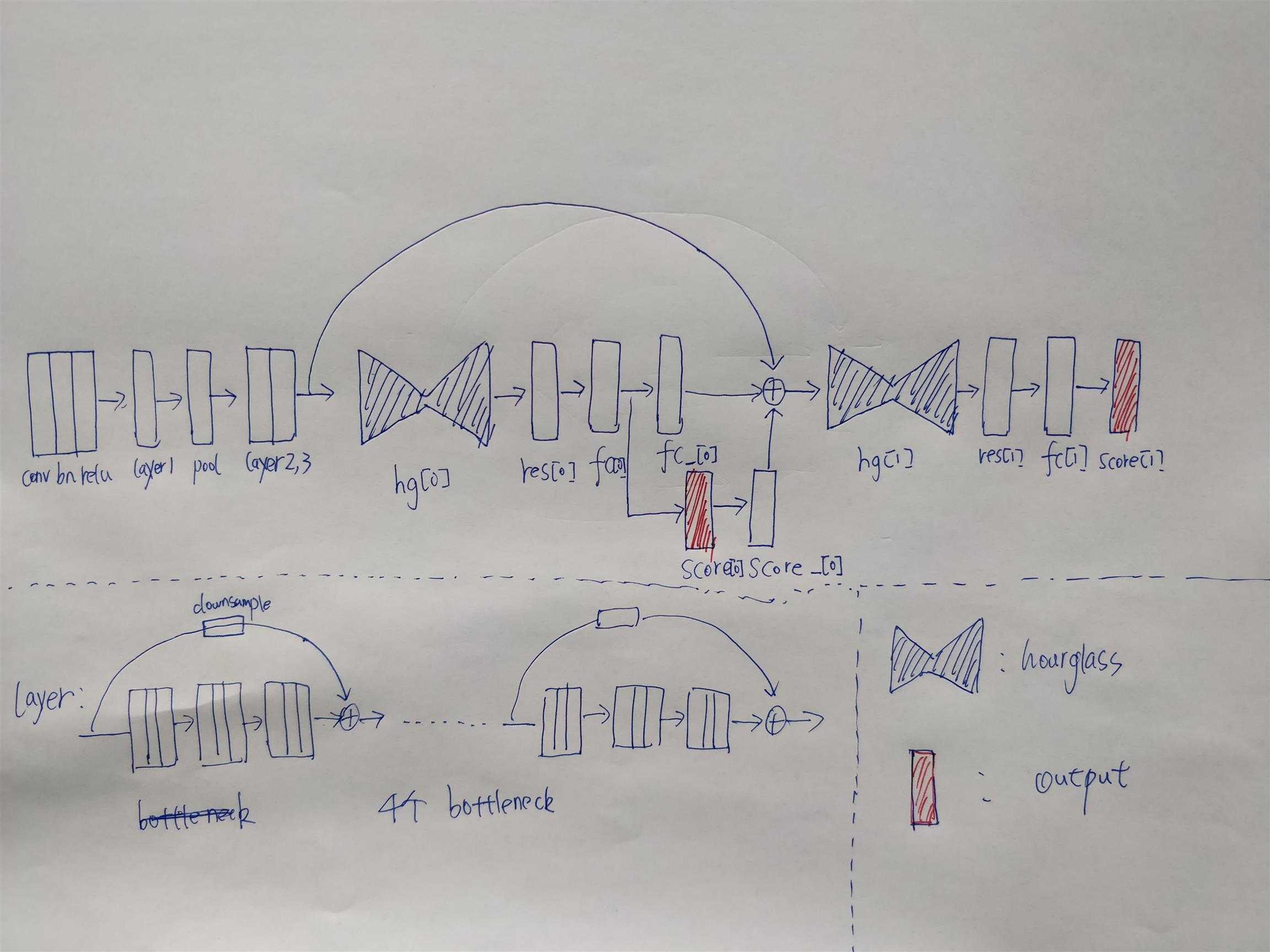
而在叠两层之前，显然需要对feature进行降维， 作者这里也是比较粗暴，用了三个大的layer，每个layer用4个基本的bottleneck，所以一共是12个bottleneck对图像进行降维以及提取high-level的feature，这个作者也在paper说明了，因为关键点检测依赖于高层次的语义信息，所以需要多加一些网络层。

实际上到这里，网络的参数已经少了，但是作者后面还跟了两个hourglass结构，每个hourglass网络结构后面跟一个输出，如上图的红色部分，所以作者实际上有两个输出，相当与是对中间提前加上监督信息

上图中的一个hourglass后面跟了一个res模块，res模块是由4个bottleneck组成，不太清楚作者这里为何还用一个res模块

以及fc模块进行通道融合，最后score模块来保证正输出的channel和ground truth是一样的

大概就是这样的