线段树---区间修改

Posted 2022-06-19 jjl0229

首先的区间增值和区间改值差别很大。

区间增值

思路：

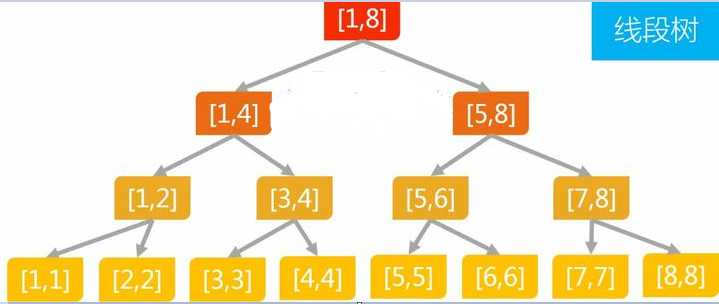
为每个节点引入一个懒标记，例如在[1,8]区间内,更新[3,5]，更新时只需将5节点（[3,4]）,12节点（[5]），标记并更新，以及他们的父节点更新。当查询到一个被标记的区间，若查询区间完全包含它时只需下放标记，更新本节点的值，然后退出（因为懒嘛，不直接访问不更新）。若更新一个区间的过程中，若已存在一个标记，下放这个标记，直到子区间上有标记而父区间没有（其实没有这部操作也可以，因为查询时会清除查询区间的所有节点，两个标记并不冲突，只是加快了查询速度）。例如，查询[2,4]。（标记的作用可以理解为此节点的子节点需要更新）

 

 

代码： 

const int N=1e5;
int a[N],sum[N],lazy[N*4];
void init()
    memset(a,1,sizeof(a));
    memset(sum,0,sizeof(sum));
    memset(lazy,0,sizeof(lazy));

void push_up(int rt)
    sum[rt]=sum[rt<<1]+sum[rt<<1|1];

void bulid(int rt,int l,int r)
    if(l==r)
        sum[rt]=a[l];
        return ;
    
    int mid=(l+r)>>1;
    bulid(rt<<1,l,mid);
    bulid(rt<<1|1,mid+1,r);
    push_up(rt);

void push_down(int rt,int l,int r)
    if(lazy[rt])
        int m=(l+r)>>1;
        lazy[rt<<1]+=lazy[rt];
        lazy[rt<<1|1]+=lazy[rt];
        sum[rt<<1]+=lazy[rt]*(m-l+1);
        sum[rt<<1|1]+=lazy[rt]*(r-m);
        lazy[rt]=0;
    

void update(int rt,int l,int r,int ll,int rr,int v)
    if(ll<=l&&r<=rr)　　//递归边界：查询区间完全包含当前区间 
        lazy[rt]+=v;　　　　//标记（次代码中，lazy有值，说明节点被更新，子节点没更新）
        sum[rt]+=v*(r-l+1);　　//更新当前节点
        return ;  　　//　因为懒，所以更新到此即可
    
    push_down(rt,l,r);　　//当lazy[rt]有值，更新子区间,将标记下传到子节点，清除当前节点标记。没有这段也可以
    int m=(l+r)>>1;
    if(ll<=m) update(rt<<1,l,m,ll,rr,v);
    if(rr>m) update(rt<<1|1,m+1,r,ll,rr,v);
    push_up(rt); //回溯 更新父节点

long long query(int rt,int l,int r,int ll,int rr)
    if(ll<=l&&r<=rr) return sum[rt];
    push_down(rt,l,r); //检查lazy，看节点是否更新,否则更新节点，清空标记
    int m=(l+r)>>1;
    long long res=0;
    if(ll<=m) res+=query(rt<<1,l,m,ll,rr);
    if(rr>m) res+=query(rt<<1|1,m+1,r,ll,rr);
    return res;

 太晚了，改值明天写吧