An overnight dance in discotheque题解

Posted 2022-06-18 ljk123-de-bo-ke

An overnight dance in discotheque题解

其实可以看做一道结论题：只将覆盖次数为2的圆放到另一组。

我们可以将结论分解为两部分：

1.将覆盖次数为2的圆放到另一组。

2.不将覆盖次数大于2的圆放到另一组

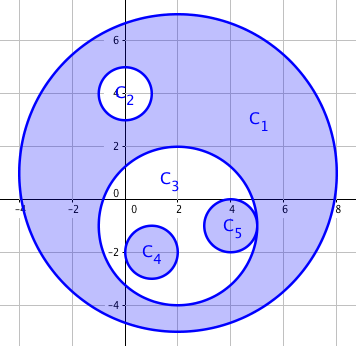
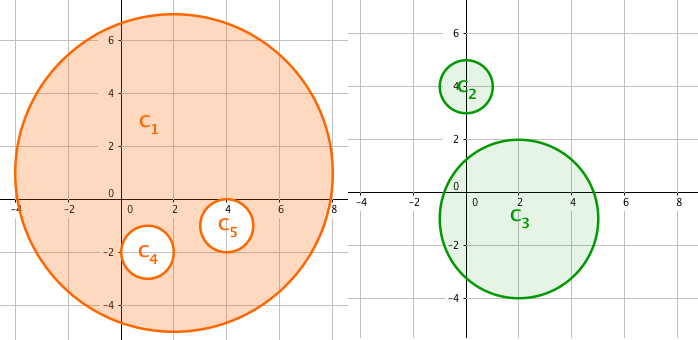
在图中我们可以看到，覆盖次数为2的圆c3被放到另一空间，

此操作增加的面积为2(S圆c3-(S圆c4+S圆c5)[即S阴影<原来的>])=2S空<原来的>

覆盖次数为2的圆，S圆肯定大于等于S阴影<原来的>，S空<原来的>一定大于等于0，

就算里面的圆也有一些放放到另一组，S圆也一定定大于等于S阴影，故一定放。

将覆盖次数为2的圆放到另外一空间后，

原来覆盖次数大于2的圆，我们对任意互相包含的一组进行讨论。

若每组最外围的圆原先覆盖次数为奇数，即为阴影，则

放到另一空间，阴影变成空，空变成阴影，变化后的S阴影仍然小与S在外围的圆=S阴+S空（现在的）
减小的量为S空（现在的），S阴之前的。

而原先被这一组包括，却没有放到另一空间的，

若最外围为阴影，不变。

否则，增量<=S最外围的圆<=S阴（放到另一空间的之前的）(即减少量)，故不放。

若每组最外围的圆原先覆盖次数为偶数，即为空，

现在的空就是之前的空，不变，则第一空间的增量<=S最外围的圆，另一空间的减少量等于S最外围的圆，故也不放。
得证

没有画图工具，口胡说得很绕，敬请理解。

大家还是感性理解一下算了。

贴一下代码：

#include<bits/stdc++.h>
using namespace std;
const int N=1006;
int n,cnt=0,f[N],rr[N],head[N];
struct edgeint nxt,to;e[N];
struct circlelong long x,y,r;o[N];
double ans=0.00,pai=3.1415926535898;
inline void add(int u,int v)e[++cnt].nxt=head[u],e[cnt].to=v,head[u]=cnt;
inline int read()
   int T=0,F=1; char ch=getchar();
   while(ch<'0'||ch>'9')if(ch=='-') F=-1; ch=getchar();
   while(ch>='0'&&ch<='9') T=(T<<3)+(T<<1)+(ch-48),ch=getchar();
   return F*T;

bool check(int u,int v)
     double t=sqrt((o[u].x-o[v].x)*(o[u].x-o[v].x)+(o[u].y-o[v].y)*(o[u].y-o[v].y));
     return (1.0000*o[v].r>=t+o[u].r);

void dfs(int u,int d,long long v)
     if(d==2) v*=-1;
     ans+=v*pai*o[u].r*o[u].r;
     for(int i=head[u];i;i=e[i].nxt) dfs(e[i].to,d+1,-v); 

bool cmp(circle u,circle v)return u.r>v.r;
int main()
    n=read();
    for(int i=1;i<=n;++i) f[i]=n+1,rr[i]=1e7,o[i].x=read(),o[i].y=read(),o[i].r=read();
    sort(o+1,o+n+1,cmp);
    for(int i=1;i<=n;++i)
        for(int j=1;j<i;++j)
            if(check(i,j)&&o[j].r<rr[i]) f[i]=j,rr[i]=o[j].r;
    for(int i=1;i<=n;++i) add(f[i],i);
    dfs(n+1,0,-1),printf("%.9lf",ans);
    return 0;