最短路总结

Posted 2022-06-18 philo-zhou

 

 

 

 

 

---恢复内容开始---

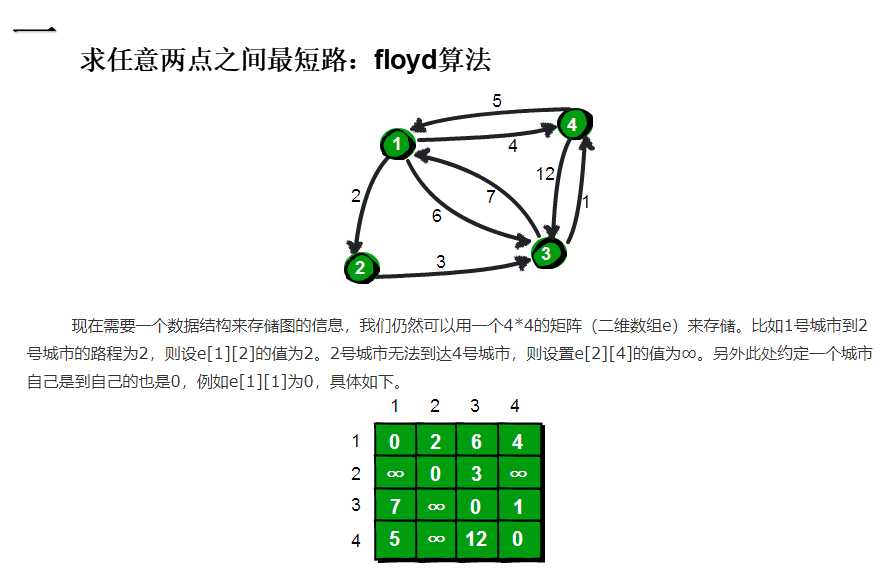
看到的结论：E是边数，n是点数量。

Dijkstra（迪杰斯特拉）：适用于权值为非负的图的单源最短路径，优先队列优化 O(E+nlgn)

SPFA：适用于权值有负值，且没有负环的图的单源最短路径，SPFA的最坏情况是O(Vn).

Floyd（弗洛伊德）：任意两点之间的最短路径。O（n^3)

给出结论：
(1)单源最短路，当权值为非负时，用Dijkstra,。
(2)单源最短路，当权值有负值，且没有负环，则用SPFA，SPFA能检测负圈，但是不能输出负圈。
(3)数据小，无负环，任意两点之间的距离。弗洛伊德

弗洛伊德

 

 

 

二 迪杰斯特拉

朴实无华迪杰斯特拉

#define inf 0x3f3f3f3f
const int N = 100;
int ma[N][N];
int vis[N], dis[N], ne[N];

void dijkstra(int u)
    memset(dis, inf, sizeof(dis));
    memset(vis, 0, sizeof(vis));
    int st = u;
    for(int i = 1; i <= n; i++)
        dis[i] = min(dis[i], ma[st][i]);
    
    for(int i = 1; i < n; i++)
        int mi = inf;
        for(int j = 1; j <= n; j++)
            if(!vis[j] && mi > dis[j])
                st = j;
                mi = dis[j];
            
        
        vis[st] = 1;
        for(int i = 1; i <= n; i++)
            dis[i] = min(dis[i], dis[st] + ma[st][i]);
        
    

 

Dijkstra优化

这个是用前向星模拟vector，然后优先队列优化。
#include <bits/stdc++.h>
#define inf 0x3f3f3f
using namespace std;
const int N = 110;
int m, n, tot;
int vis[N], dis[N], ne[N];
struct node
    int  di, num; di是距离，num是编号。
;
bool operator < (node a, node b)     //重载函数，表示在优先队列里排序是怎么排的，是按照x值的从小到大排的。
      return a.di > b.di;        //从小到大，这个定义是>，是相反的。

struct qq
    int u, v, w, next;
 p[110000];
void add(int u, int v, int w)
    p[++tot] = (qq)u, v, w, ne[u];
    ne[u] = tot;

void betterdis(int st)

    priority_queue<node> q;
    dis[st] = 0;
    q.push((node)0,st);
    while(q.size())
    
        node now = q.top();
        q.pop();
        if(vis[now.num]) continue;
        else vis[now.num] = 1;
        for(int i = ne[now.num]; i != 0; i = p[i].next)
        
            int u = p[i].u, v = p[i].v, w = p[i].w;
            if(!vis[v] && dis[v] > dis[u] + w)
            
                dis[v] = dis[u] + w;
                q.push((node)dis[v], v);
            
        
    

int main()

    while(cin>> n >> m)
    
        memset(dis, inf, sizeof(dis));
        memset(ne, 0, sizeof(ne));
        memset(vis, 0, sizeof(vis));
        memset(p, 0, sizeof(p));
        tot = 0;
        for(int i = 1; i <= m; i++)
        
            int u, v, w;
            cin >> u >> v >> w;
            add(u, v, w);
            add(v, u, w); //无向图
        
        betterdis(1);       算的是从1到其他点的距离。
        cout << dis[n] << endl;
    
    return 0;

 

---恢复内容结束---