公钥密码学

Posted 2020-07-28 block2016

意义：公钥密码学的发展是整个密码学发展历史中最伟大的一次革命，也许可以说是唯一的一次革命。轮转机和DES是密码学发展的重要标志，但是它们都是基于代替和置换这些初等方法上。

提出背景：为了解决传统密码中最困难的两个问题而提出。1、密码分配；2、数字签名

特点：1、公钥算法是基于数学函数而不是基于代替和置换；2、公钥密码是非对称的，使用两个独立的密钥。

传统密码和公钥密码的区别

　　 

几个误解：

　　1、公钥密钥比传统密码安全

　　　　任何加密方法的安全性依赖于密钥长度和破译密文所需要的计算量

　　2、公钥密码将替代传统密码

　　　　由于现有公钥密码计算量大，不太可能取代传统密码，主要用在密钥管理和签名中

 

公钥密码体制

　　

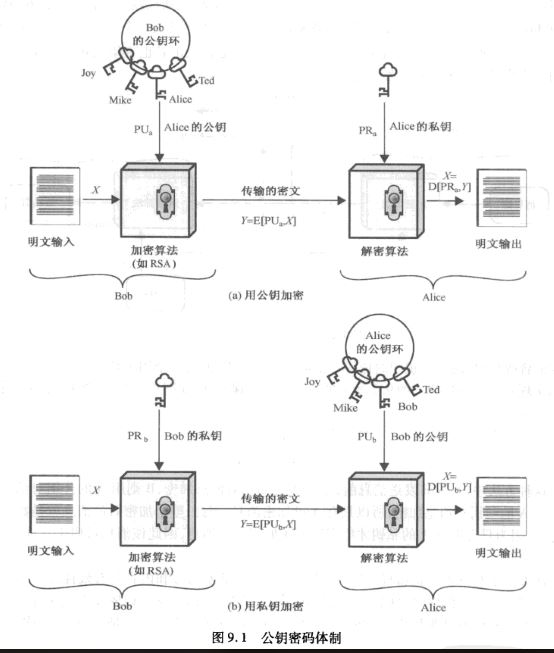
公钥算法依赖于一个加密密钥和一个与之相关的解密密钥，这些算法具有如下特点：

　　1、仅根据密码算法和加密密钥来确定解密密钥在计算上是不可行的；

　　2、对于有些算法（如RSA）还满足以下特点

　　　　两个密钥中的任何一个都可用来加密，另一个用来解密。

 

公钥密码体制有6个组成部分：明文、加密算法、公钥、私钥、密文、解密算法

其加密的主要操作步骤如下：

　　1、每个用户产生一对密钥，其中一个存于公开的寄存器或文件中以供访问，称为公钥。另一个则保持私密，称为私钥。每个用户都可以拥有很多其他用户的公钥。

　　2、若A要发消息给B，则A用B的公钥来加密消息，由于只有B有私钥，故而也只有B可以对消息解密，其他任何接受者都不能解密消息。

 

此外公钥体制还可以用于认证，具体操作如下：

　　1、A向B发送消息前，先用A的私钥对消息加密，因为B只有用A的公钥才能对消息解密，因此该消息可以用于认证源和数据完整性。

　　由于对整个消息的认证加密过于耗费计算时间和存储空间，可以对此进行改进。只对一个称为认证符的小数据块进行加密，该认证块是整个消息的函数，对该消息的任何修改必然会引起认证符的变化，因此用发送方的私钥对认证符进行加密，加密的结果可作为数字签名，它能验证消息源、消息和通信序列的有效性。

 

为了同时保证加密和认证，则需要先用发送方的私钥进行数字签名，再用接收方的公钥对整个消息进行加密。不过这种方法的缺点是每次通信中要执行四次复杂的公钥算法。

 

公钥密码体制的应用

一般，公钥密码体制的应用分三类：

　　1、加密/解密：发送方用接收方公钥对信息加密

　　2、数字签名：发送方用自身的私钥对消息“签名”

　　3、密钥交换：通信双方交换会话密钥（传统密码的密钥）

 

对公钥密码的要求

　　1、接收方B产生一对密钥在计算上是容易的

　　2、已知公钥和要加密的消息M，发送方A产生相应的密文在计算上是容易的  

　　　　C = E(PU_b,M)

　　3、接收方B使用私钥对接收的密文解密以恢复明文在计算上是容易的

　　　　M = D(PR_b,C) = D(PR_b,E(PU_b,M))

　　4、已知公钥PU_b，攻击者要确定私钥PR_b在计算上是不可行的

　　5、已知公钥PU_b和密文C，攻击者要恢复明文M在计算上是不可行的

　　6、对于部分公钥密码应用，还应满足加密和解密函数的顺序可以交换

　　　　M = D(PU_b,E(PR_b,M)) = D(PR_b,E(PU_b,M))

事实上，要满足上述条件即是要找到一个单向陷门函数。单向陷门函数满足下列性质：

　　若k和X已知，求Y = f_k(X)  容易计算

　　若k和Y已知，求X = f_k^-1(Y) 容易计算

　　若Y已知但k未知，则求X = f_k^-1(Y)是不可行的

 

以上计算上容易是指：一个问题可以在输入长度的多项式时间内得到解决，即若输入长度为n位，计算的时间复杂度为n^a，a为常数。

计算上不可行是指：解决一个问题所需时间比输入规模的多项式增长更快。如输入长度是n位，计算时间复杂度是2ⁿ。

 

公钥密码分析

　　1、穷举攻击：解决办法是使用长密钥，但是长密钥将使加密/解密变慢（公钥密码加密/解密时间对密钥长度的非线性增长），因此限制了公钥密码的应用。

　　2、根据公钥计算私钥：目前未能做数学上的证明确定该攻击不可行，但也没有可行的办法做这样的攻击。

　　3、穷举消息攻击（公钥体制特有）：根据消息本身的特点（公钥经常用来传递传统密码的密钥）来进行对消息的穷举攻击，如发送56位DES密钥。解决办法就是在要发送的消息后附加一个随机数。