斐波那契查找

Posted 2022-06-12 zhoubo123

斐波那契查找

斐波那契查找也是折半查找的一种改良版；斐波那契查找最主要的就是找mid这个点；

在该种查找算法中，我们要找的mid这个点为数组中的黄金分割点，要求黄金分割点

我们就要用到斐波那契数列了；我们可以看一下这个数列：1,1,2,3,5,8,13,21,34,55..........;

可以看出俩个规律：

1：从第三项开始每一项等于它的前两项的和；

2：数列越往后，前后两项的比值越接近0.618，也就是黄金比例的比值；

利用这两个规律我们就可以来找这个黄金分割点；我们令这个数组为F[],下标为k；

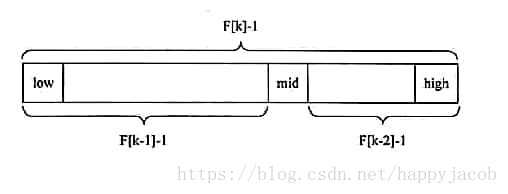
斐波那契查找的核心就是在mid前面的长度为F[k-1]-1,在mid的后面的长度为F[k-2]-1;

具体步骤：（记待查找的数组为A）

1：构建斐波那契数组；

2：找到n（A数组的长度）在斐波那契数组中的位置，并将数组补全（可用A（n-1）来补）；

3：计算mid=low+F（k-1）-1；

4：如果A[mid]>key(key为要查找的数）high=mid-1；k=k-1；（mid前面的长度）

5：如果A[mid[<key  low=mid+1；k=k-2（mid后面的长度）；

6：如果A[mid]=key &&mid<=high 则返回下标值（即mid的值）；否则查找失败；

 

#include<iostream>
using namespace std;
int max_size=20;
void fbnq_list(int *A)//构建斐波那契数组； 

    A[0]=A[1]=1;
    for(int i=2;i<20;i++)
    
        A[i]=A[i-1]+A[i-2];
    

int fbnq_search(int A[],int n,int key)

    int F[max_size];
    fbnq_list(F);
    int low=0;
    int high=n-1;
    int mid=0;
    int k=0;
    while(n>F[k]-1)//找出n在斐波那契数列中的位置 
        k++;
    for(int i=n;i<F[k]-1;i++)//将数组补全，大于n的下标对于的数全部为A【high】； 
        A[i]=A[high];
    while(low<=high)
    
        mid=low+F[k-1]-1;//mid的位置为黄金分割点； 
        if(A[mid]>key)
        
            high=mid-1;
            k=k-1;//F[k-1]-1为mid前面的元素个数； 
        
        else if(A[mid]<key)
        
            low=mid+1;
            k=k-2;//F[k-1] -1为mid后面的元素个数； 
        
     else
        
            if(mid <= high)//如果为真则找到相应的位置
                return mid;
            else
                return -1;
        
    
    return -1;
    

int main()

    int A[]=-1,2,3,45,54,78,95,102,158,458,1651,1656400;
    int key;
    cin>>key; 
    int x=fbnq_search(A,12,key);
    if(x!=-1) cout<<x;//输出所对应的下标； 
    else cout<<"没有该元素"; 
    return 0;

 

斐波那契查找是折半查找的升级版，那么也要求序列是有序的序列；

在最坏情况下，斐波那契查找的时间复杂度还是O(log2n)，且其期望复杂度也为O(log2n)，

但是与折半查找相比，斐波那契查找的优点是它只涉及加法和减法运算，而不用除法，

而除法比加减法要占用更多的时间，因此，斐波那契查找的运行时间理论上比折半查找小，

但是还是得视具体情况而定。