B树与B+详解

Posted 2022-06-11 jing99

一、前言

　　动态查找树主要包括：二叉查找树，平衡二叉树，红黑树，B树，B-树，查找的时间复杂度就为O(log₂N)，通过对数就可以发现降低树的深度就会提高查找效率。在大数据存储过程，大量的数据会存储到外存磁盘，外存磁盘中读取与写入某数据的时候，首先定位到磁盘中的某一块，这就有个问题：如何才能有效的查找磁盘中的数据呢，这就需要一种高效的外存数据结构，也就引出了下面的课题。

　　B树为了存储设备或者磁盘而设计的一种平衡查找树，与红黑树类似（拓展会讲）。

　　拓展：

　　B树与红黑树的

　　不同在于：B树的节点可以有很多子女，从几个到几万个不等，

　　相同：一颗含有n个节点的B树高度和红黑树是一样的，都是O(lgn)。

二、定义

　　1.B树

　　（1）一棵m阶的B树，特性如下：

　　利用书面的定义（参考书籍-《数据结构》）

　　1）树中的每个结点最多含有m个孩子；

　　2）除了根结点和叶子结点，其他结点至少有[ceil(m / 2)（代表是取上限的函数）]个孩子；

　　3）若根结点不是叶子结点时，则至少有两个孩子（除了没有孩子的根结点）

　　4）所有的叶子结点都出现在同一层中，叶子结点不包含任何关键字信息；

　　B树的类型与节点定义

    /**
     * B树中的节点。
     */
    private static class BTreeNode<K, V> 
        /**
         * 节点的项，按键非降序存放
         */
        private List<Entry<K, V>> entries;
        /**
         * 内节点的子节点
         */
        private List<BTreeNode<K, V>> children;
        /**
         * 是否为叶子节点
         */
        private boolean leaf;
        /**
         * 键的比较函数对象
         */
        private Comparator<K> kComparator;

        private BTreeNode() 
            entries = new ArrayList<>();
            children = new ArrayList<>();
            leaf = false;
        
        ... ...

　　2.B+树

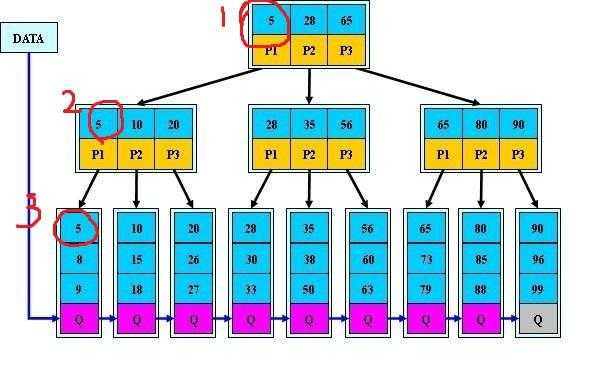
　　B+树可以说是B树的一种变形，它把数据都存储在叶结点，而内部结点只存关键字和孩子指针，因此简化了内部结点的分支因子，B+树遍历也更高效，其中B+树只需所有叶子节点串成链表这样就可以从头到尾遍历，其中内部结点是并不存储信息，而是存储叶子结点的最小值作为索引，下面将讲述到。

　　定义：参考数据《数据结构》与百度百科

　　B+树用于数据库和文件系统中，NTFS等都使用B+树作为数据索引，

　　1）有n棵子树的结点含有n个关键字，每个关键字都不会保存数据，只会用来索引，并且所有数据都会保存在叶子结点；

　　2）所有的叶子结点包含所有关键字信息以及指向关键字记录的指针，关键字自小到大顺序连接；

　　　　　　　　　　

三、问答

　　1.为什么说B+树比B树更适合做操作系统的数据库索引和文件索引？

　　（1）B+树的磁盘读写的代价更低

　　　　B+树内部结点没有指向关键字具体信息的指针，这样内部结点相对B树更小。

　　（2）B+树的查询更加的稳定

　　　　因为非终端结点并不是最终指向文件内容的结点，仅仅是作为叶子结点中关键字的索引。这样所有的关键字的查找都会走一条从根结点到叶子结点的路径。所有的关键字查询长度都是相同的，查询效率相当。 

四、B树与B+树操作

　　1.B树

　　1.1 B树的插入

　　B树的插入是指插入一条记录，如果B树已存在需要插入的键值时，用新的值替换旧的值；若B树不存在这个值时，则是在叶子结点进行插入操作。

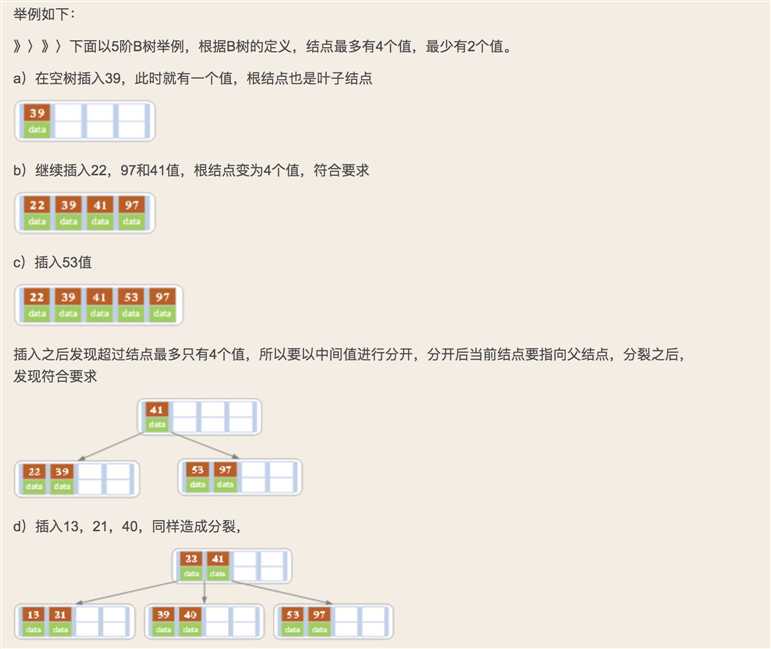
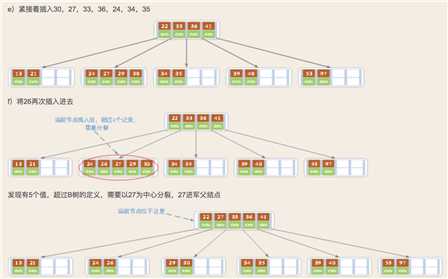
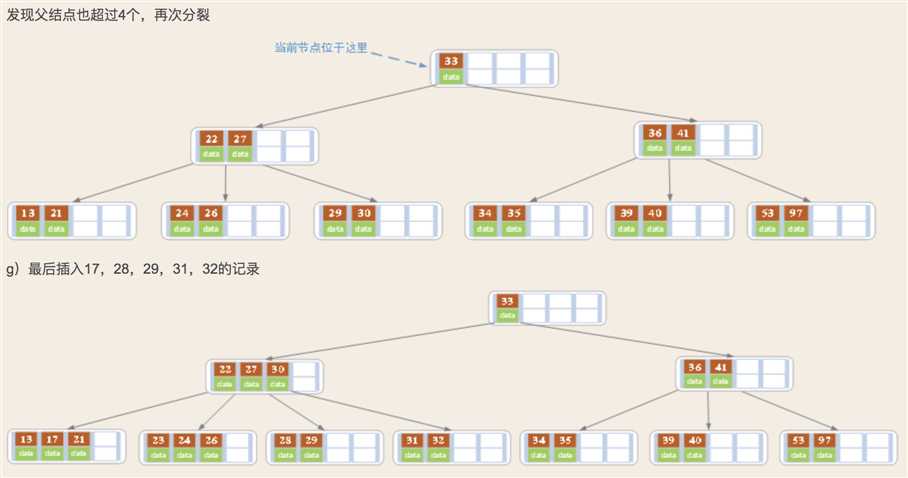
　　对高度为h的m阶B树，新结点一般插第h层。通过检索可以确定关键码应插入的位置，

　　1）若该结点中关键码个数小于m-1，则直接插入就可

　　2）若该结点中关键码个数等于m-1，则将引起结点的分裂，以中间的关键码为界将结点一分为二，产生了一个新的结点，并将中间关键码插入到父结点中；

　　重复上述过程，最坏情况一直分裂到根结点， 建立一个新的根结点，整个B树就增加一层。

　

   

　

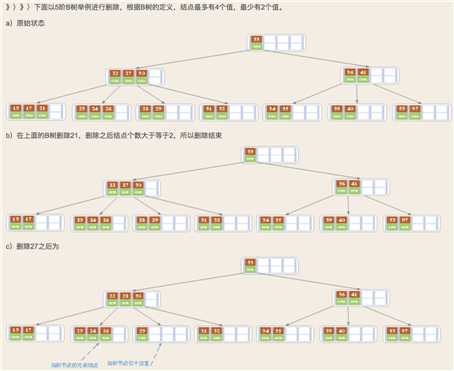
　　1.2 B树的删除

　　B树删除：首先要查找该值是否在B树中存在，如果存在，判断该元素是否存在左右孩子结点，如果有，则上移孩子结点中的相近结点（左孩子最右边的结点或者有孩子最左边的结点）到父结点中，然后根据移动之后的情况；如果没有，进行直接删除；如果不存在对应的值，则删除失败。

　　1）如果当前要删除的值位于非叶子结点，则用后继值覆盖要删除的值，再用后继值所在的分支删除该后继值。（该后继值必须位于叶子结点上）

　　2）该结点值个数不小于Math.ceil(m/2)-1（取上线函数），结束删除操作，否则下一步

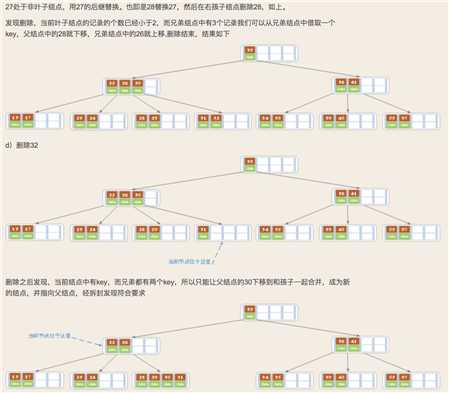
　　3）如果兄弟结点值个数大于Math.ceil(m/2)-1，则父结点中下移到该结点，兄弟的一个值上移，删除操作结束。

　　将父结点的key下移与当前的结点和他的兄弟姐妹结点key合并，形成一个新的结点，

　　有些结点可能有左兄弟，也有右兄弟，我们可以任意选择一个兄弟结点即可。

   

　

　　2.B+树

　　2.1 B+树的插入

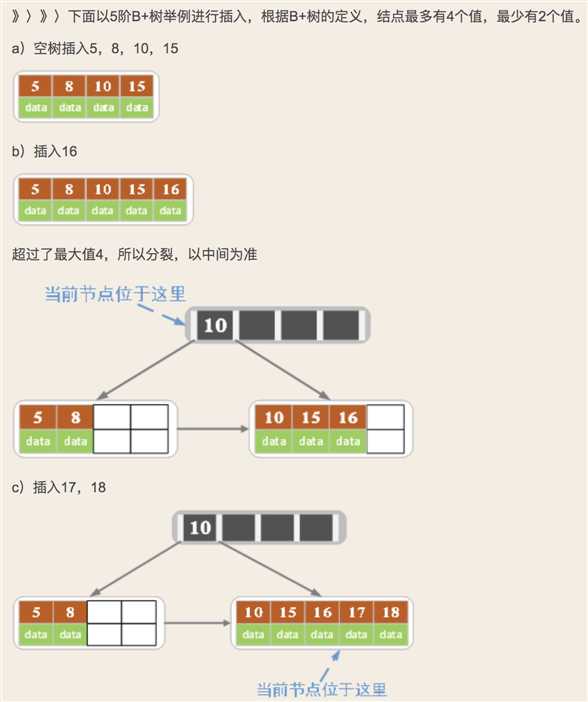
　　B+树插入：

　　1）若为空树，直接插入，此时也就是根结点

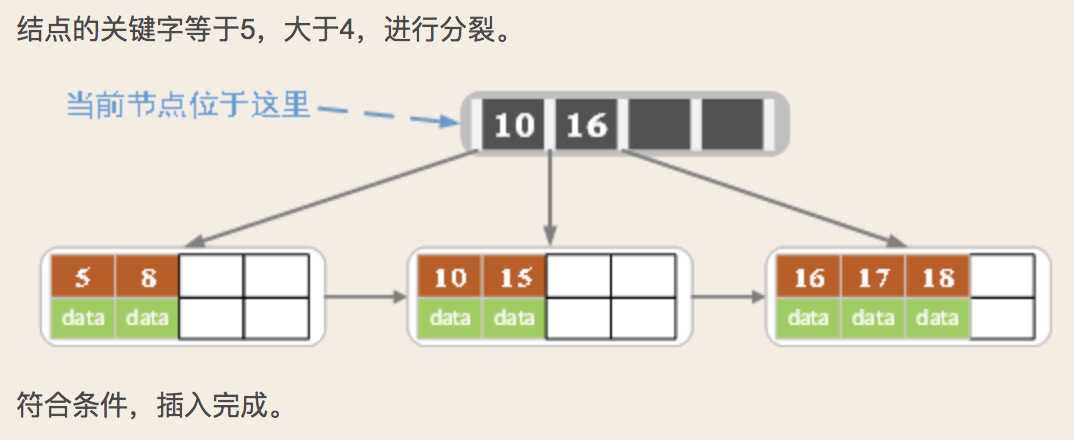
　　2）对于叶子结点：根据key找叶子结点，对叶子结点进行插入操作。插入后，如果当前结点key的个数不大于m-1，则插入就结束。反之将这个叶子结点分成左右两个叶子结点进行操作，左叶子结点包含了前m/2个记录，右结点包含剩下的记录key，将第m/2+1个记录的key进位到父结点中（父结点必须是索引类型结点），进位到父结点中的key左孩子指针向左结点,右孩子指针向右结点。

　　3）针对索引结点：如果当前结点key的个数小于等于m-1，插入结束。反之将这个索引类型结点分成两个索引结点，左索引结点包含前(m-1)/2个数据，右结点包含m-(m-1)/2个数据，然后将第m/2个key父结点中，进位到父结点的key左孩子指向左结点, 父结点的key右孩子指向右结点。
　

　

　　2.2 B+树删除

　

　

　

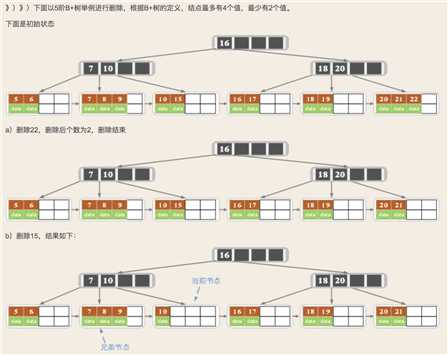
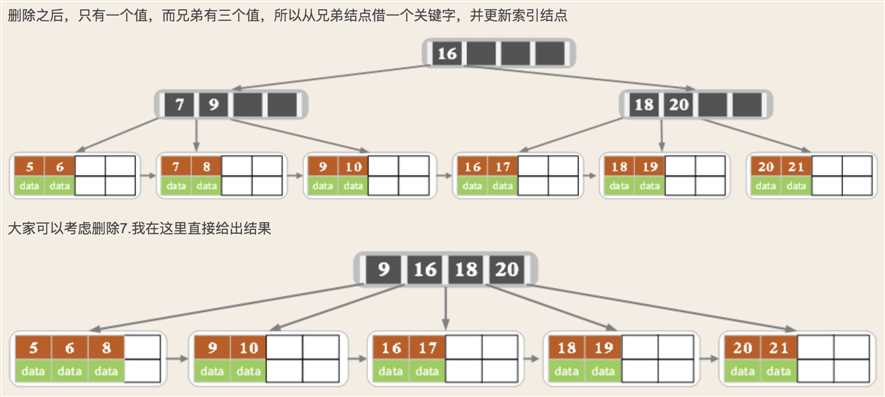
　　以上就是B树和B+树的操作。