[数学]卡特兰数

Posted 2022-06-10 linzhengmin

前言

咕比赛写博客的我。哭哭。
在本篇文章的剩余部分中，我们定义\\(C(n)\\)为卡特兰数的第\\(n\\)项

定义

翻阅了一堆文章，也没找到真正的定义，暂且拿这个充当定义:
\\(C(n)\\)表示，从原点出发，每次向x或y轴正方向移动1单位，到达点(n,n)，且在移动过程中不越过第一象限平分线的移动方案数。

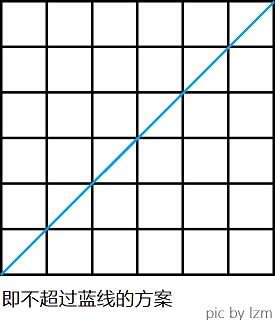
通项公式

我们记\\(C(n)\\)为卡特兰数的第\\(n\\)项
\\[C(n)= \\left( \\beginmatrix2n \\\\ n\\endmatrix \\right) - \\left( \\beginmatrix2n \\\\ n + 1\\endmatrix \\right)\\]

证明

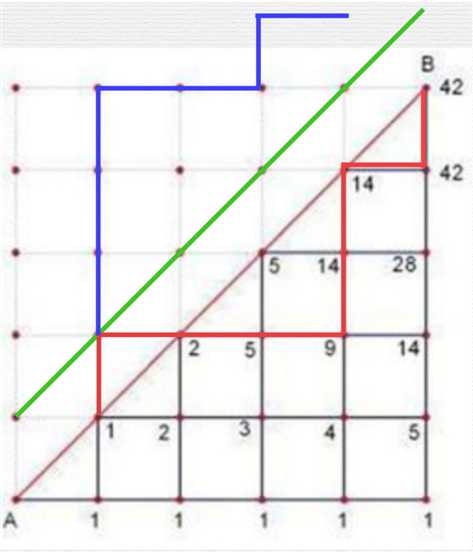
首先根据组合数学，我们知道如果不考虑第一象限平分线的限制，方案数为\\(\\left(\\beginmatrix2n \\\\ n\\endmatrix\\right)\\)。
注意到任何一种非法的方案，都至少有一个点\\(p\\)碰到了直线\\(y=x+1\\)，那么我们将这条路径在\\(p\\)点以上的在直线\\(y=x+1\\)以下的部分沿直线\\(y=x+1\\)镜像到直线\\(y=x+1\\)上。
看图理解:上图中的绿线为\\(y=x+1\\)，红线为原非法路径在\\(p\\)上的部分，蓝线为镜像后的结果。
我们会发现任何一种非法方案都可以变换成(0,0)到(n-1,n+1)的一条路径，且存在一一映射关系，所以总方案数为:\\(\\left(\\beginmatrix2n \\\\ n\\endmatrix\\right)-\\left(\\beginmatrix2n \\\\ n+1\\endmatrix\\right)\\)

化简

\\[C(n)=\\left(\\beginmatrix2n \\\\ n\\endmatrix\\right)-\\left(\\beginmatrix2n \\\\ n+1\\endmatrix\\right)\\]
\\[=\\frac(2n)!n!n!-\\frac(2n)!(n+1)!(n-1)!\\]
\\[=\\frac1n+1(\\frac(2n)!(n+1)n!n!-\\frac(2n)!n!(n-1)!)\\]
\\[=\\frac1n+1(\\frac(2n)!(n+1)n!n!-\\frac(2n)!\\times nn!n!)\\]
\\[=\\frac1n+1\\frac(2n)!(n+1)-(2n)! \\times nn!n!\\]
\\[=\\frac1n+1\\frac(2n)!n!n!\\]
\\[=\\frac1n+1\\left(\\beginmatrix2n \\\\ n\\endmatrix\\right)\\]

变形

\\[C(n)=\\frac1n+1\\sum_i=0^n\\left(\\beginmatrixn \\\\ i \\endmatrix\\right)^2\\]

递推

\\[C(n+1)=\\sum_i=0^nC(i)C(n-i),\\ C(0)=1\\]
\\[C(n+1)=\\frac2(2n+1)n+2C(n),\\ C(0)=1\\]

应用

1. n对括号的合法配对方案书
2. n个节点的二叉树的形态数
3. n+1个叶子(n个非叶节点)的满二叉树的形态数, 走到左儿子+1,走到 右儿子-1,类似于括号匹配(大致同2)
4. n个数入栈后出栈的排列总数
5. 对凸n+2边形进行不同的三角形分割的方案数(分割线断点仅为顶点，且分割线仅在顶点上相交)
6. n层的阶梯切割为n个矩形的切法数

卡特兰数与OI初赛

首先背诵上述应用场景，然后记忆卡特兰数的前几项:1,1,2,5,14,42,132。

拓展

\\(n+m\\)个人排队买票，并且满足\\(n \\geq m\\)，票价为50元，其中n个人有且仅有一张\\(50\\)元钞票，m个人有且仅有一张\\(100\\)元钞票，初始时候售票窗口没有钱，问有多少种排队的情况数能够让大家都买到票。
如果\\(n=m\\)可以直接用Catalan数解决，也就是将有50元的人看成是上述应用中的左括号，有100元的人看成是右括号。
对与\\(n>m\\)的情况，假设所有人都可以买到票的情况数是\\(A_n,m\\)，不能让每个人都买到的情况数是\\(B_n,m\\)，设最早买不到票的人为\\(p\\)，他一定手持100元且售票处没有50元，那么这时将前p个人的钱从50元变成100元，从100元变成50元(不考虑顺序，所以没有影响)，这时候就有\\(n+1\\)个人有50元，\\(m-1\\)个有100元的，所以就得到\\(B_n,m=\\left(\\beginmatrixn+m \\\\ n+1\\endmatrix\\right)\\)，那么\\(A_n,m=\\left(\\beginmatrixn+m \\\\ n\\endmatrix\\right)-\\left(\\beginmatrixn+m \\\\ n+1\\endmatrix\\right)\\)。
这正是应用了上文证明的"翻折"思想。