HDU2019多校K - Function (推式子）

Posted 2022-06-02 zhangbuang

 

 

 

 

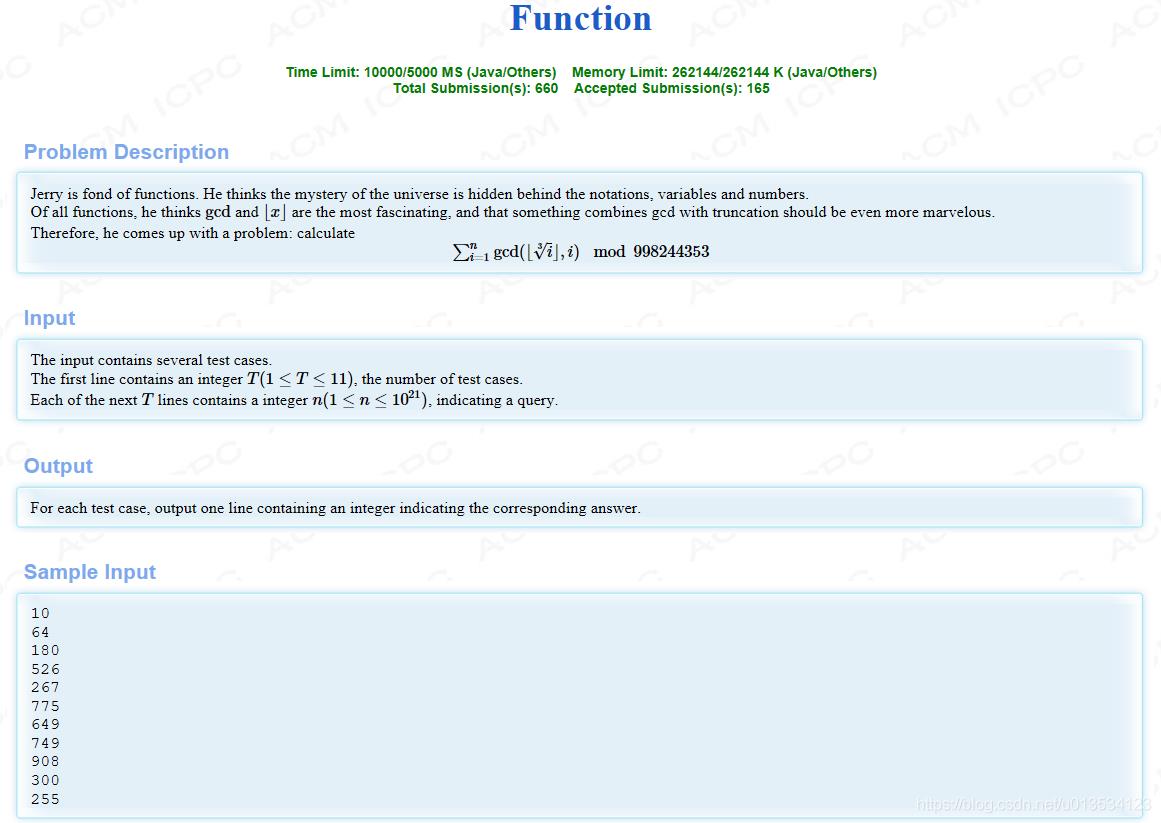
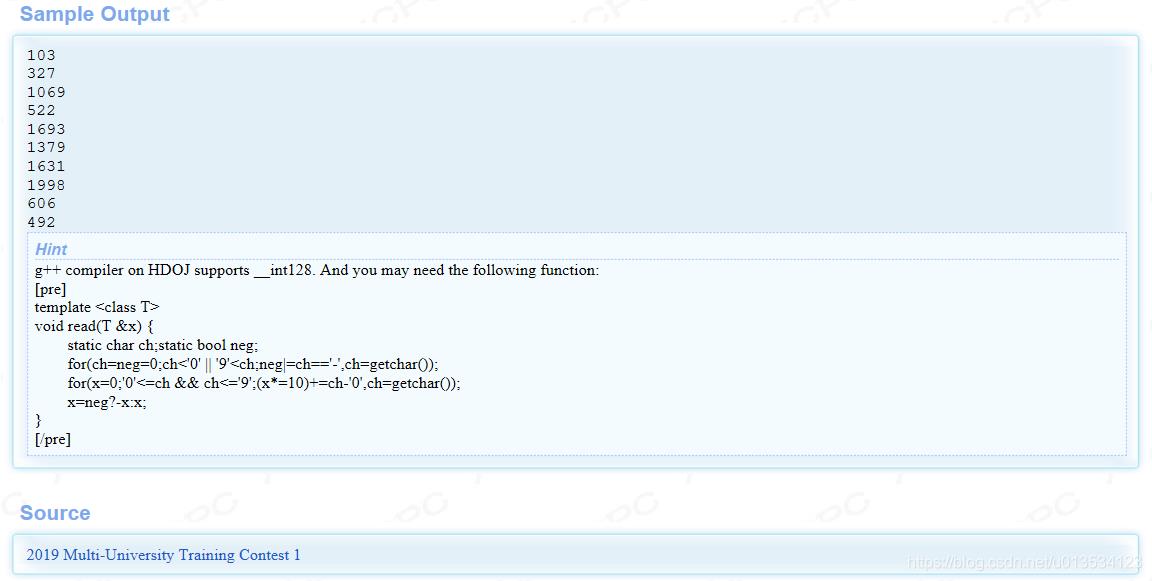
SOLUTION:

https://www.90yang.com/2019hdu-multi1-k-function/

phi 卷 id 不会线性筛

https://www.cnblogs.com/DeaphetS/p/11228116.html

phi 卷 id 不会线性筛  这有一个nlogn的筛法

 

#include <bits/stdc++.h>
typedef long long lld;
using namespace std;
const size_t MAXN = 1e7+5;
const int MOD = 998244353;
bool isnp[MAXN];
int pcn, pri[MAXN/10];
lld g[MAXN];
lld p[MAXN];
int phi[MAXN], q[MAXN];
int mod;

void init_prime()

    g[1] = q[1] = phi[1] = 1;

    for (int i = 2; i < MAXN; i++)
    
        if (!isnp[i])
        

            q[i] = i-1;
            phi[i] = i-1;
            pri[pcn++] = i;
        

        for (int j = 0; j < pcn; j++)
        
            int k = i * pri[j];
            if (k >= MAXN) break;
            isnp[k] = true;

            if (i % pri[j] == 0)
            
                q[k] = q[i] * pri[j];
                phi[k] = phi[i] * pri[j];
                break;
            
            else
            
                phi[k] = phi[i] * (pri[j] - 1);
                q[k] = q[pri[j]];
            
        
    

   for(int d=1;d*d<MAXN;d++) // 就是枚举一个因子d，他是一些数的小于等于sqrt这个数的因子
      for(int n=d*d;n<MAXN;n+=d)
         
           p[n]=(p[n]+1ll*d*phi[n/d])%MOD;
         if(d*d<n)p[n]=(p[n]+1ll*(n/d)*phi[d])%MOD;
        
    
    for (int i = 1; i < MAXN; i++)
    
        g[i] = (g[i-1] + i + (3 * i + 3) * (g[i] % MOD)) % MOD;
    


int two(__int128 n)

    if (n < 8) return 1;
    int l = 1, r = 1e9+7, m;
    while (r - l > 1)
    
        m = (l + r) >> 1;
        if (m > n / m / m)
            r = m;
        else
            l = m;
    
    return r-1;


void solve()

    __int128 n = 0;
    char buf[30];
    scanf("%s", buf);
    for (int i = 0; buf[i]; i++)
        n = n * 10 + (buf[i] - ‘0‘);
    int m = two(n);
    lld ans = g[m-1];
    __int128 qwq = m; qwq *= m; qwq *= m; qwq -= 1;

    ans=0;

    for(int i=1;i<m;i++)
    
        ans+=i; ans%=MOD;
        ans += p[i]*(3*i+3)%MOD;
        
    

    for (int i = 1; i * i <= m; i++)
    
        if (m % i == 0)
        
            ans += phi[i] * ((n / i % MOD) - (qwq / i % MOD)) % MOD;
            if (m != i * i)
                ans += phi[m / i] * (n / (m / i) % MOD - (qwq / (m / i) % MOD)) % MOD;
        
    
    ans %= MOD;
    if (ans < 0) ans += MOD;
    printf("%lld\\n", ans);


int main()

    init_prime();
    int T;
    scanf("%d", &T);
    while (T--) solve();
    return 0;