二叉树的重建

Posted 2022-05-31 zlhdbk

二叉树的三种遍历方式

1.按照根结点，左子树，右子树的顺序输出结点编号，这称为树的前序遍历（Preorder Tree Walk）

2.按照左子树，根结点，右子树的顺序输出结点编号，这称为树的中序遍历（Inorder Tree Walk）

3.按照左子树，右子树，根结点的顺序输出结点编号，这称为树的后序遍历（Postorder Tree Walk）

所有的遍历方式都是递归的

注意:二叉树的遍历会对树的每个结点进行一次访问，因此算法复杂度为O(n)。但使用递归实现遍历算法时要注意，一旦树的结点数量庞大且分布不均，很可能导致递归深度过深。

前序遍历先访问根结点，然后前序遍历左子树，再前序遍历右子树

中序遍历先遍历根结点的左子树，再访问根结点，最后中序遍历右子树

后序遍历是从后往前，先左子树，再右子树，最后结点。

以上三个遍历方法的特点，我们可以总结出来Pre的第一个元素即为二叉树的根，Pro的最后一个元素也为二叉树的根。

那么已知前序和中序遍历的情况下，设Preorder遍历的当前结点为c,c在in中的位置为m，则m左侧就是c的左子树，右侧就是右子树，然后同理递归。

举一个例子

Preorder的输入为pre=1，2，3，4，5，6，7，8，9，Inorder的输入为in=3，2，5，4，6，1，8，7，9；

例如当前结点为1，其在in中为3 2 5 4 6 [1] 8 7 9，那么当前树的根就是1，左右子数就是3 2 5 4 6和 8 7 9，接下来在3 2 5 4 6组成的树中，Preorder遍历的下一个结点2是根（3 [2] 5 4 6），3和5 4 6 是两个子树，那么我们就可以得到如下图的一个二叉树。

 

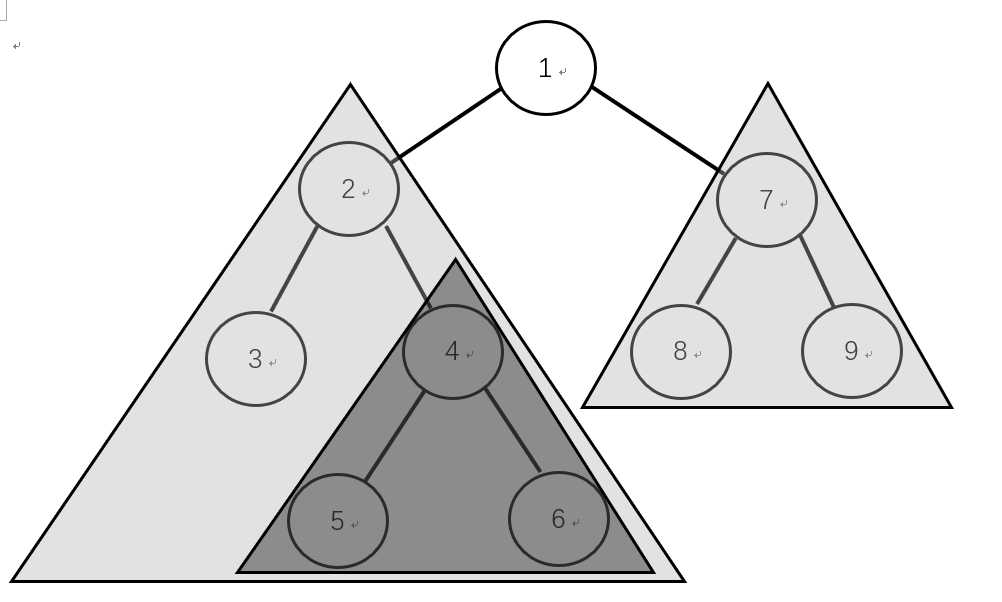
已知前序和中序遍历，可以确定一棵二叉树。已知中序和后序遍历，可以确定一棵二叉树。但是，已知前序和后序遍历，不能确定一棵二叉树。

洛谷P1030 求先序排列（已知中序和后序）

 

这个题目是根据一棵树的中序和后序排列求出其的先序排列，同上面的方法一样，首先我们还是需要把这个二叉树建立出来。

 先根据样例（第一行为中序，第二行为后序）来看一下解题的思路

求先序排列其实是一个不断的找根的一个过程，首先我们根据后序遍历的性质可以知道主根为A，那么找到中序遍历中的A，根据中序遍历的性质我们知道A的中序遍历的左子树为B，右子树为DC，对应可以找到A的后序遍历的左子树为B，右子树为DC，那么问题就变成了求

1.中序遍历B,后序遍历B的树      2.中序遍历DC，后序遍历DC的树

再根据后序遍历的方法，找到两个根B，和C然后以同样的方法一直递归下去就可以建成整个树。

再用一个复杂一点的例子

中序ACGDBHZKX，后序CDGAHXKZB，首先可找到主根B，同理可将中序遍历分为ACGD和HZKX两棵子树，对应可找到后序遍历CDGA和HXKZ

从而问题就变成求1.中序遍历ACGD，后序遍历CDGA的树 2.中序遍历HZKX，后序遍历HXKZ的树；

接着递归，按照原先方法，找到1.子根A，再分为两棵子树2.子根Z，再分为两棵子树。一直递归即可

 具体看代码 还不能理解的话用上面的例子手动模拟一遍会更容易理解一些

 

 

里面有用到一些string类的函数这里统一说明

str.find(x)就是返回元素x在字符串str中第一次出现的位置

str.substr(pos，n)就是获得一个从pos开始长度为n的字符串str的拷贝（pos的默认值是0，n的默认值是s.size() - pos，即不加参数会默认拷贝整个str）

 1 #include <iostream>
 2 #include <cstring>
 3 #include <string>
 4 #include <algorithm>
 5 #include <queue>
 6 #include <stack>
 7 #include <stdio.h>
 8 #include <cmath>
 9 #include <string.h>
10 #include <vector>
11 
12 #define ll long long
13 using namespace std;
14 void solve(string in,string post)//递归找根
15 
16     if(!in.size())
17     return ;
18     char root=post[post.size()-1];//找到并且输出根
19     cout<<root;
20     int i=in.find(root);//找到根在中序中的位置从而分左右子树
21     //cout<<i<<endl;
22     solve(in.substr(0,i),post.substr(0,i));//左子树的中序遍历和后序遍历
23     solve(in.substr(i+1),post.substr(i,in.size()-i-1));//右子树的中序遍历和后序遍历
24 
25 int main()
26 
27     //freopen("C:\\\\Users\\\\16599\\\\Desktop\\\\in.txt","r",stdin);
28     string in,post;
29     cin>>in>>post;
30     solve(in,post);
31     return 0;
32 

 PS：后期如果做到根据前序和中序输出后序的题目的话会再加进去