[算法模版]莫队

Posted 2022-05-31 gavinzheng

[算法模版]莫队

莫队是一个极其有意思的玄学算法，常用于暴力骗分。

首先，莫队是通过暴力转移区间来求解答案的。那么显然，完成单组询问复杂度是\\(O\\left(x^*(|r 1-r 2|+|(l1-l2 |))\\right.\\)。其中\\(x\\)为每次的转移复杂度。

莫队算法的总复杂度是\\(n \\sqrt m\\)。（虽然我也不知道怎么证的）

莫队的精髓在于将序列分块，块的大小也因题而异。对于不带修的普通莫队，最优分块方法是

而对于带修改的莫队，分块方法是：

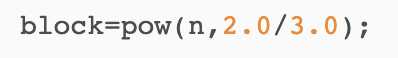
带修莫队只要添加一个第三关键字——按照时间排序即可。

再介绍一种极其玄学的奇偶优化：

我们只需把

int cmp(query a, query b) 
    return belong[a.l] == belong[b.l] ? a.r < b.r : belong[a.l] < belong[b.l];

换成

int cmp(query a, query b) 
    return (belong[a.l] ^ belong[b.l]) ? belong[a.l] < belong[b.l] : ((belong[a.l] & 1) ? a.r < b.r : a.r > b.r);

即可。

具体原理见：莫队——奇偶优化详解

---

这里放一道莫队+玄学优化卡常能过的暴力题。

[SDOI2009]HH的项链

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#define maxn 500500
using namespace std;
int block[maxn],val[maxn],n,m,cnt[1020000],tot,ans[maxn];
struct gg 
    int l,r,id;
q[500500];
inline void add(int col) 
    if(!cnt[col])tot++;
    cnt[col]++;

inline void del(int col) 
    if(cnt[col]==1)tot--;
    cnt[col]--;

inline bool cop(gg x,gg y)return (block[x.l]^block[y.l])?x.l<y.l:((block[x.l]&1)?(x.r<y.r):(x.r>y.r));
int main() 
    scanf("%d",&n);
    for(int i=1;i<=n;i++)scanf("%d",&val[i]);
    scanf("%d",&m);
    int bl=n/sqrt(m*2/3);
    for(int i=1;i<=n;i++)block[i]=(i-1)/bl+1;
    for(int i=1;i<=m;i++)scanf("%d%d",&q[i].l,&q[i].r);q[i].id=i;
    sort(q+1,q+1+m,cop);
    int l=1,r=1;cnt[val[1]]++;tot=1;
    for(int i=1;i<=m;i++) 
        int tl=q[i].l,tr=q[i].r;
        while(tl<l)l--;add(val[l]);
        while(r<tr)r++;add(val[r]);
        while(l<tl)del(val[l]);l++;
        while(tr<r)del(val[r]);r--;
        ans[q[i].id]=tot;
    
    for(int i=1;i<=m;i++)printf("%d\\n",ans[i]);