神经网络DNN ——正则化

Posted 2022-05-30 dwithy

一、过拟合与正则化作用

1、先了解什么是过拟合

了解什么是过拟合问题，以下面图片为例，我们能够看到有两个类别，蓝色是分类曲线模型。

 

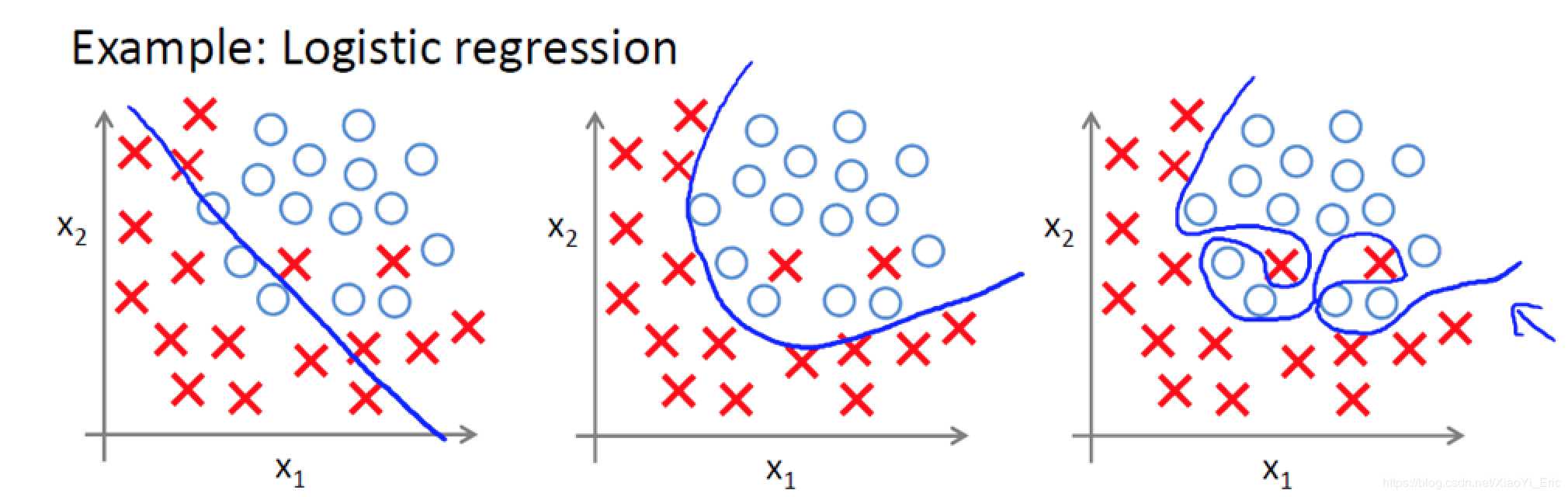
• 欠拟合：图1分类，不能很好的将X和O很好的分类，属于欠拟合。
• 正拟合：图2有两个X被误分类，但是大部分数据都能很好的分类，误差在可接受范围内，分类效果好，属于良好的拟合模型。
• 过拟合：图3虽然能够全部分类正确，但分类曲线明显过于复杂，模型学习的时候学习了过多的参数项，但其中某些参数项是无用的特征。当我们进行识别测试集数据时，就需要提供更多的特征，如果测试集包含海量的数据，模型的时间复杂度可想而知。

2、正则化作用

模型过拟合是因为模型过于复杂，可以通过对特征变量系数的调整来避免过拟合，而引入正则化正是为了实现这个目的，具体如何实现将在下一节说明。

常见的正则化方法有这几种：

• 当参数是向量的时候（如logistics回归，参数为$\\left (\\theta _i:\\theta _1,\\theta _2,...,\\theta _n  \\right )$），有L1正则化、L2正则化。

• 当参数是矩阵的时候（如神经网络的权重矩阵W），这时候用的是F-1范数正则化、F-2范数正则化，现在基本都是使用F-2范数正则化比较多。
• 神经网络还有Drop正则化。
• 增加训练集的数据量可以避免过拟合，另外有些模型可以用集成学习的Bagging、boost方法来进行正则化。

 

二、神经网络的正则化

1、矩阵的F-1范数、F-2范数（Frobenius范数，注意：这里和logistics回归的L1、L2正则化的向量范数不一样）

• 矩阵的F-1范数：矩阵所有元素的绝对值之和：

$$\\left \\| W \\right \\|_1=\\sum_i,j\\left |\\omega _i,j  \\right |$$

• 矩阵的F-2范数：矩阵所有元素的平方求和后开根号：

$$\\left \\| W \\right \\|_2=\\sqrt\\sum_i,j\\left (\\omega _i,j  \\right )^2$$

 

2、L1正则化与L2正则化

假设神经网络的损失函数为J(W,b)，参考逻辑回归的正则化，是在损失函数J(W,b)后面加一个正则化项，神经网络DNN也是一样的，只是变成了加F-范数，L1正则化与L2正则化如下所示：

$$L2: J(W,b)+\\frac\\lambda 2m\\sum_l\\epsilon L\\left \\| W \\right \\|_2=J(W,b)+\\frac\\lambda 2m\\sum_l\\epsilon L\\sqrt\\sum_i,j\\left (\\omega _i,j  \\right )^2$$

$$L1: J(W,b)+\\frac\\lambda 2m\\sum_l\\epsilon L\\left \\| W \\right \\|_1=J(W,b)+\\frac\\lambda m\\sum_l\\epsilon L\\sum_i,j\\left |\\omega _i,j  \\right |$$

这里m为样本数，l为各个隐藏层，$\\lambda$为超参数，需要自己调试。

 

3、以L2正则的权重衰减防止过拟合

由于L1正则与L2正则原理相似，而且大多数神经网络模型使用L2正则，所以这里以L2为例来说明为什么能防止过拟合。

直观理解：

原损失函数$J(W,b)$加上正则项$\\frac\\lambda 2m\\sum_l\\epsilon L\\left \\| W \\right \\|_2$之后的新损失函数$J(W,b)^‘=J(W,b)+\\frac\\lambda 2m\\sum_l\\epsilon L\\left \\| W \\right \\|_2$，在使用梯度下降训练模型时，目标是要最小化新的损失函数$ J(W,b)^‘$，我们在训练前先设置超参数$\\lambda$，若设置较大的超参数$\\lambda=0.9$，则相对于设置较小的超参数$\\lambda=0.1$，我们需要更小的权重F-2范数$\\left \\| W \\right \\|_2$才能够使得我们达到最小化$ J(W,b)^‘$的目的。所以如果我们使用较大的超参数$\\lambda$的时候，会使得W整体变得更加的稀疏，这样就可以使得W的影响减少，从而避免了由于模型过于复杂导致的过拟合。

 

公式推导：

$$新损失函数：J(W,b)^‘=J(W,b)+\\frac\\lambda 2m\\sum_l\\epsilon L\\left \\| W \\right \\|_2$$