DP专题——棋盘分割

Posted 2022-05-17 nelson992770019

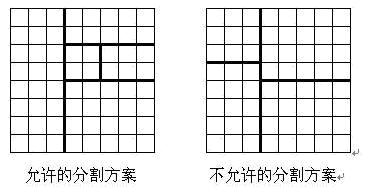
题目：https://www.luogu.org/problem/P1436 题目描述 将一个８*８的棋盘进行如下分割：将原棋盘割下一块矩形棋盘并使剩下部分也是矩形，再将剩下的两部分中的任意一块继续如此分割，这样割了(n-1)次后，连同最后剩下的矩形棋盘共有n块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行) 原棋盘上每一格有一个分值，一块矩形棋盘的总分为其所含各格分值之和。现在需要把棋盘按上述规则分割成n块矩形棋盘，并使各矩形棋盘总分的平方和最小。 请编程对给出的棋盘及n，求出平方和的最小值。 输入格式 第1行为一个整数n(1 < n < 15)。 第2行至第9行每行为8个小于100的非负整数，表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。 输出格式 仅一个数，为平方和。

　　一道典型的dp题，思路很简单，我们用（a,b,c,d）来描述左上角为(a,b),右下角为（c,d）的矩形，对于每个矩形，我们考虑竖着切一刀or横着切一刀，每次考虑切下来的两块哪一块作为下次切的对象即可。

　　优化：用sum[i][j]描述（1,1,i,j）的面积，求某个矩形面积用容斥即可。

上代码：

 

 1 #include<iostream>
 2 #include<cstdio> 
 3 #include<cmath>
 4 using namespace std;
 5 const int inf=1e9;
 6 int n;
 7 int ma[20][20];
 8 int sum[20][20];
 9 int dp[20][20][20][20][20];
10 int cal(int a,int b,int c,int d)
11     return sum[c][d]+sum[a-1][b-1]-sum[c][b-1]-sum[a-1][d];
12 
13 int main()
14     scanf("%d",&n);
15     for(int i=1;i<=8;i++)
16         for(int j=1;j<=8;j++)
17             scanf("%d",&ma[i][j]);
18             sum[i][j]=sum[i-1][j]+sum[i][j-1]+ma[i][j]-sum[i-1][j-1];
19         
20     
21     for(int a=1;a<=8;a++)
22         for(int b=1;b<=8;b++)
23             for(int c=a;c<=8;c++)
24                 for(int d=b;d<=8;d++)
25                     dp[a][b][c][d][0]+=cal(a,b,c,d);
26                     dp[a][b][c][d][0]*=dp[a][b][c][d][0];
27                 
28             
29         
30     
31     for(int t=1;t<n;t++)
32     for(int a=1;a<=8;a++)
33         for(int b=1;b<=8;b++)
34             for(int c=a;c<=8;c++)
35                 for(int d=b;d<=8;d++)
36                     int q=inf;
37                     for(int y=b;y<d;y++)
38                         q=min(q,min(dp[a][b][c][y][0]+dp[a][y+1][c][d][t-1],dp[a][y+1][c][d][0]+dp[a][b][c][y][t-1]));
39                     
40                     for(int x=a;x<c;x++)
41                         q=min(q,min(dp[x+1][b][c][d][0]+dp[a][b][x][d][t-1],dp[x+1][b][c][d][t-1]+dp[a][b][x][d][0]));//这两句容易错，注意考虑切入点与区间关系
42                     
43                     dp[a][b][c][d][t]=q;
44                 
45             
46         
47     
48 //     for(int i=1;i<=8;i++)
49 //        for(int j=1;j<=8;j++)
50 //            cout<<sum[i][j]<<" ";
51 //        
52 //        cout<<endl;
53 //    
54     cout<<dp[1][1][8][8][n-1]<<endl;
55     return 0;
56