深度学习面试题21:批量归一化(Batch Normalization,BN)
Posted itmorn
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了深度学习面试题21:批量归一化(Batch Normalization,BN)相关的知识,希望对你有一定的参考价值。
目录
BN的由来
BN的作用
BN的操作阶段
BN的操作流程
BN可以防止梯度消失吗
为什么归一化后还要放缩和平移
BN在GoogLeNet中的应用
BN在GoogLeNet中的应用
|
BN的由来 |
BN是由Google于2015年提出,论文是《Batch Normalization_ Accelerating Deep Network Training by Reducing Internal Covariate Shift》,这是一个深度神经网络训练的技巧,主要是让数据的分布变得一致,从而使得训练深层网络模型更加容易和稳定。所以目前BN已经成为几乎所有卷积神经网络的标配技巧了。
|
BN的作用 |
Internal Convariate shift是BN论文作者提出来的概念,表示数据的分布在网络传播过程中会发生偏移,我们举个例子来解释它,假设我们有一个玫瑰花的深度学习网络,这是一个二分类的网络,1表示识别为玫瑰,0则表示非玫瑰花。我们先看看训练数据集的一部分:

直观来说,玫瑰花的特征表现很明显,都是红色玫瑰花。 再看看训练数据集的另一部分:

很明显,这部分数据的玫瑰花各种颜色都有,其特征分布与上述数据集是不一样的。
通俗地讲,刚开始的数据都是同一个分布的,模型学习过程中,模型的参数已经适合于一种分布,突然又要适应另一种分布,这就会让模型的参数发生很大的调整,从而影响到收敛速度和精度,这就是Internal covariate shift。
而BN的作用就是将这些输入值或卷积网络的张量进行类似标准化的操作,将其放缩到合适的范围,从而加快训练速度;另一方面使得每一层可以尽量面对同一特征分布的输入值,减少了变化带来的不确定性。
|
BN的操作阶段 |
某一批次的张量通过卷积层并加上偏置后,relu激活之前,即

|
BN的操作流程 |
假设某一批次的数据为2个2行2列2深度的张量,BN的过程如下:
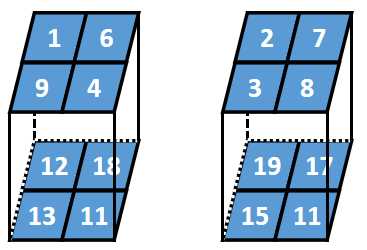
第一步:
计算每一层深度的均值和方差
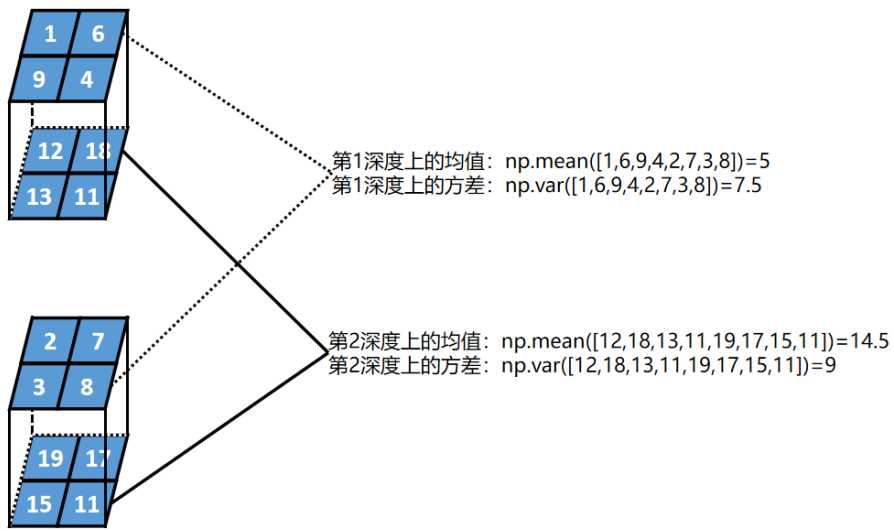
第二步:
对每一层设置2个参数,γ和β。假设第1深度γ=2、β=3;第2深度γ=5、β=8。
计算公式:

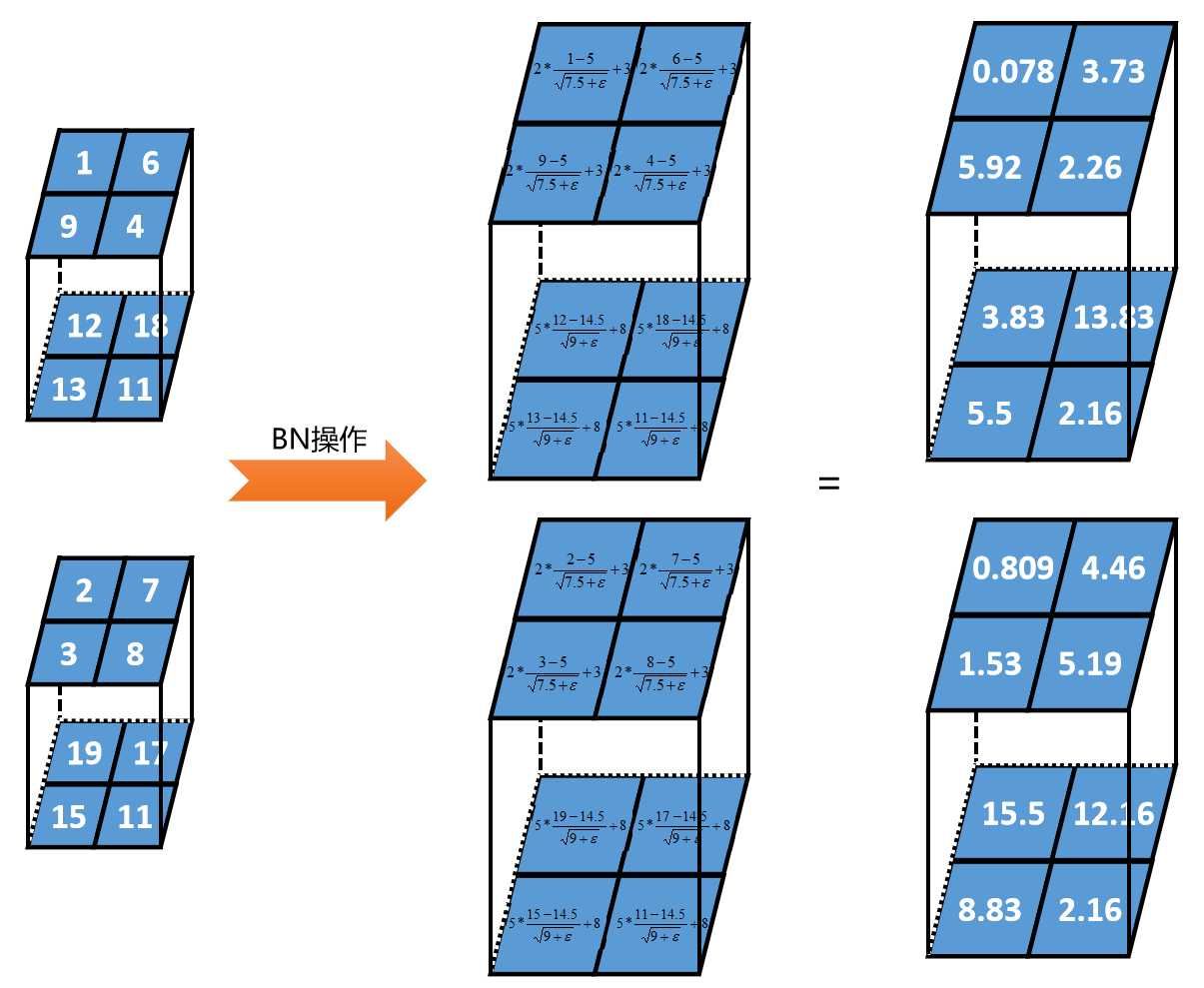
|
BN可以防止梯度消失吗 |
BN可以防止学习过程中梯度消失,这一点论文中有阐述,作者说可以如果使用sigmod激活函数的时候,如果不用BN的话,会让反向传播的过程中梯度消失(当输出值较大或较小时,sigmod函数就会进入饱和区域,导致其导数几乎为零),但是可以通过使用Relu激活函数来解决,那就意味着BN主要还是让数据分布变为一致。
|
为什么归一化后还要放缩和平移 |
如果激活函数选择的sigmod函数,我们知道多层线性神经网络其实可以用一层线性网络来表示,那我们使用BN算法将输入值投射到激活函数的线性区域,会不会使得深度网络效果下降呢?答案是肯定的,如果仅仅是归一化各层输入值到一个近似的线性区域,我们的深层网络能力将大大降低。
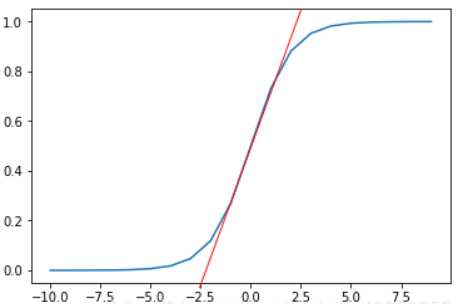
因此,BN算法其实还有另一个步骤,那就是再将归一化的数据放大,平移回非线性区域。
但是个人感觉如果选用了relu激活函数,这个缩放和平移影响不大
PS:γ和β也是待学习的参数,在网络学习的过程中会被更新

|
BN在GoogLeNet中的应用 |
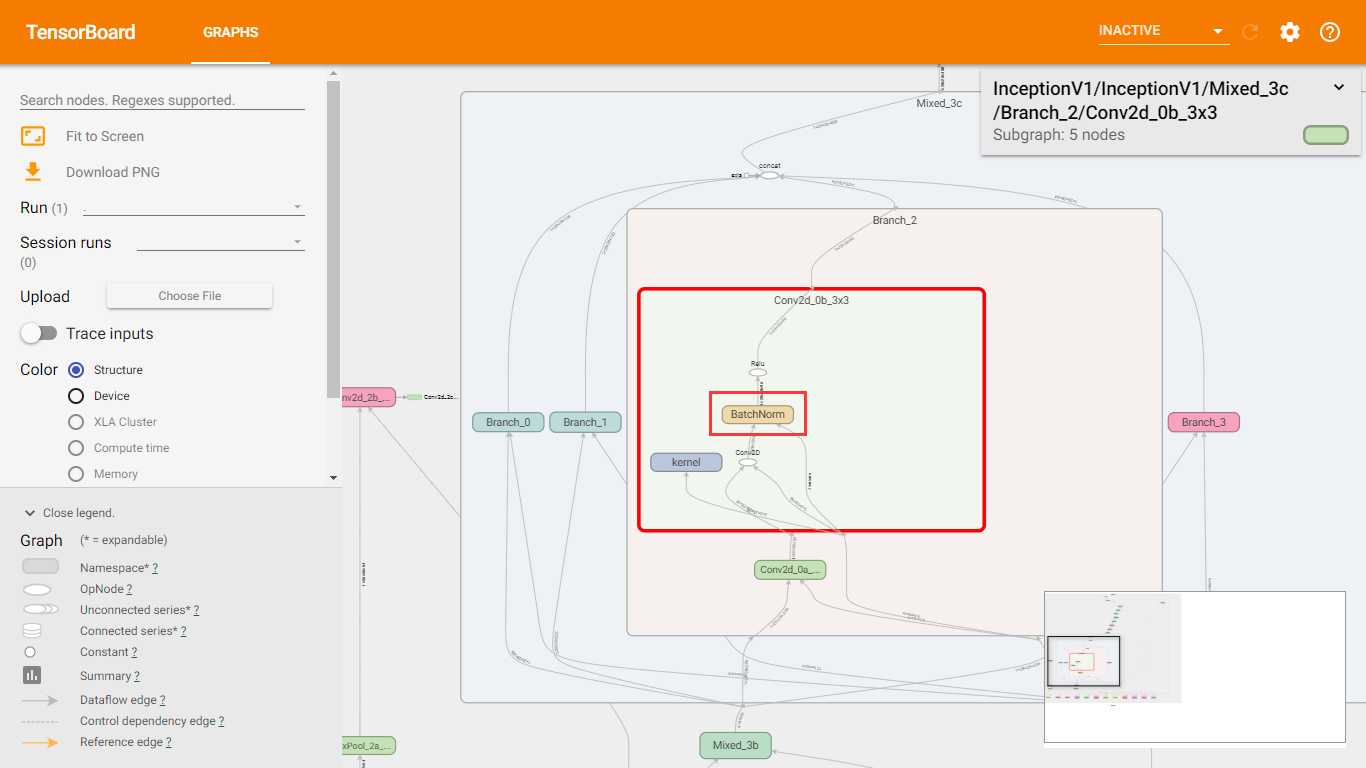
在slim中,BN已经用在了InceptionV1中了,如下图所示。
BN是2015年提出的,InceptionV1是2014年提出的,但是slim的代码是2016年完成的。在Inception的其他版本中也有应用BN。
|
参考资料 |
《图解深度学习与神经网络:从张量到TensorFlow实现》_张平
inceptionV1-Going Deeper with Convolutions
《深-度-学-习-核-心-技-术-与-实-践》
【深度学习】批归一化(Batch Normalization)
https://www.cnblogs.com/skyfsm/p/8453498.html
深度学习基础系列(七)| Batch Normalization
https://www.cnblogs.com/hutao722/p/9842199.html
深度学习 --- 优化入门四(Batch Normalization(批量归一化)一)
https://blog.csdn.net/weixin_42398658/article/details/84560411
以上是关于深度学习面试题21:批量归一化(Batch Normalization,BN)的主要内容,如果未能解决你的问题,请参考以下文章