[Comet OJ - Contest #4 D][39D 1584]求和_"数位dp"

Posted 2022-05-10 shurak

求和

题目大意：

数据范围：

---

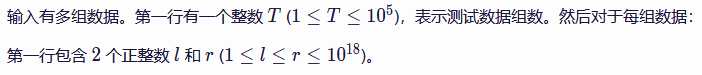
题解：

脑筋急转弯可还行.....

我们发现只需要最后枚举个位/xk/xk

因为前面的贡献都是确定的了。

故此我们最后暴力统计一下就好咯。

不知道为啥我组合数一直过不去，暴力求过了呜呜。

代码：

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;

char *p1, *p2, buf[100000];

#define nc() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1 ++ )

ll rd() 
	ll x = 0;
	int f = 1;
	char c = nc();
	while (c < 48) 
		if (c == ‘-‘)
			f = -1;
		c = nc();
	
	while (c > 47) 
		x = (((x << 2) + x) << 1) + (c ^ 48), c = nc();
	
	return x * f;


int a[20], cnt, b[20];

ll C[20][20];

void init() 
	C[0][0] = 1;
	for (int i = 1; i <= 19; i ++ ) 
		C[i][0] = 1;
		for (int j = 1; j <= i; j ++ ) 
			C[i][j] = (C[i - 1][j] + C[i - 1][j - 1]) % 10;
		
	


inline ll f(ll x) 
	cnt = 0;
	while (x) 
		a[ ++ cnt] = x % 10;
		x /= 10;
	
	ll mdl = 0;
	for (int i = cnt; i >= 2; i -- ) 
		(mdl += C[cnt - 1][i - 1] * a[i] % 10) %= 10;
	
	return mdl;


// inline ll f(ll x) 
// 	cnt = 0;
// 	for (; x; x /= 10)
// 		a[cnt ++ ] = x % 10;
// 	reverse(a, a + cnt);
// 	while(cnt != 1) 
// 		int m = 0;
// 		for (int i = 1; i < cnt; i ++ ) 
// 			int c = (a[i] + a[i-1]) % 10;
// 			if(!m && !c) continue;
// 			b[m ++ ] = c;
// 		
// 		if (!m)
// 			b[m ++ ] = 0;
// 		cnt = m;
// 		for (int i = 0; i < cnt; i ++ )
// 			a[i] = b[i];
// 	
// 	return a[0];
// 

ll calc(ll x) 
	if (x < 10ll) 
		return (x + 1) * x / 2;
	
	ll ans = x / 10 * 45;
	ll mdl = f(x / 10 * 10);
	// cout << mdl << endl ;
	int tmp = x % 10;
	for (int i = 0; i <= tmp; i ++ ) 
		ans += (mdl + i) % 10;
	
	return ans;


int main() 
	int T = rd();
	init();
	while (T -- ) 
		ll l = rd(), r = rd();
		printf("%llu\\n", calc(r) - calc(l - 1));
	
	return 0;

 

小结：真·脑筋急转弯.....