卡特兰数总结

Posted 2022-05-02 oi-zzyy

tip：

　　卡特兰数是组合数学中经常出现在计数问题的数列，出栈次序是卡特兰数的一个应用。 我们将入栈视为 +1，出栈视为 -1，则限制条件为在任意位置前缀和不小于 0。

　　卡特兰数公式：

 

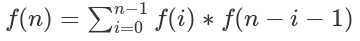
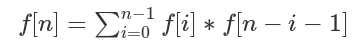
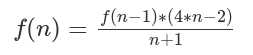
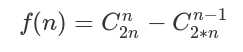
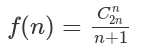
　　卡特兰数前几项为：1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452。

实战：

T1：「BZOJ3907」网格

题干：

　　某城市的街道呈网格状，左下角坐标为 A(0,0)，右上角坐标为 B(n,m)，其中 n≥m。现在从 A(0,0) 点出发，只能沿着街道向正右方或者正上方行走，且不能经过图示中直线左上方的点，即任何途径的点 (x,y) 都要满足 x≥y，请问在这些前提下，到达 B(n,m) 有多少种走法。

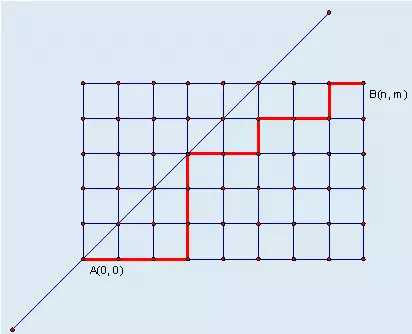
题解：

　　一道 catalan 裸题。但是 n 不一定等于 m，所以我们就需要变换一下 catalan 的式子。catalan 的定义式就是两个组合数相减的形式，是一个单步容斥。

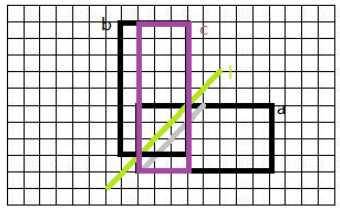
　　看一下上图，我们单步容斥减去的就是不合法的情况（紫框）。不合法的情况一定会碰到黄线，我们可以将碰到黄线以后的部分进行沿黄线翻折，这个翻折后的路径一定在紫框内，减去即可。即：

$ans=C_n+m^n-C_n+m^m-1$