test

Posted 2022-04-26 nickchen121

　　　　在循环神经网络(RNN)模型与前向反向传播算法中，我们总结了对RNN模型做了总结。由于RNN也有梯度消失的问题，因此很难处理长序列的数据，大牛们对RNN做了改进，得到了RNN的特例LSTM（Long Short-Term Memory），它可以避免常规RNN的梯度消失，因此在工业界得到了广泛的应用。下面我们就对LSTM模型做一个总结。

1. 从RNN到LSTM

　　　　在RNN模型里，我们讲到了RNN具有如下的结构，每个序列索引位置t都有一个隐藏状态\\(h^(t)\\)。

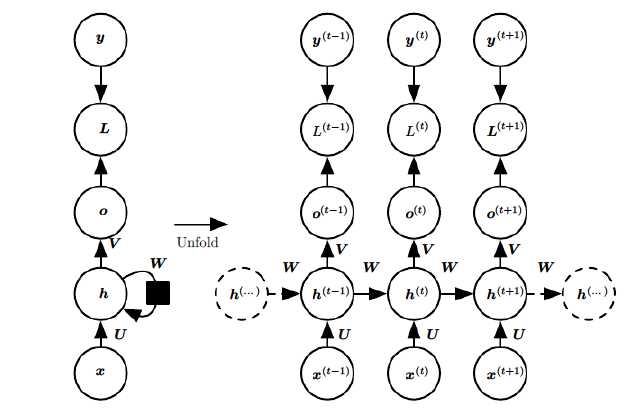
　　　　如果我们略去每层都有的\\(o^(t), L^(t),?y^(t)\\)，则RNN的模型可以简化成如下图的形式：

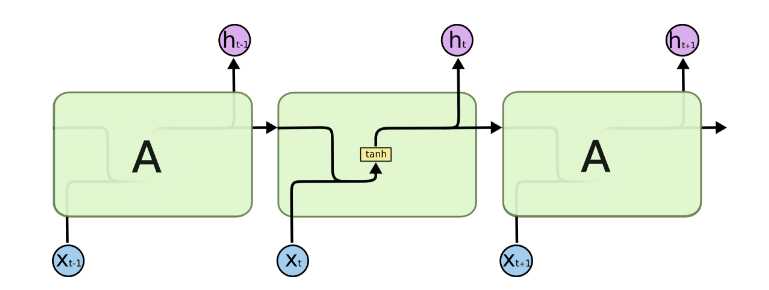
　　　　图中可以很清晰看出在隐藏状态\\(h^(t)\\)由\\(x^(t)\\)和\\(h^(t-1)\\)得到。得到\\(h^(t)\\)后一方面用于当前层的模型损失计算，另一方面用于计算下一层的\\(h^(t+1)\\)。
　　　　由于RNN梯度消失的问题，大牛们对于序列索引位置t的隐藏结构做了改进，可以说通过一些技巧让隐藏结构复杂了起来，来避免梯度消失的问题，这样的特殊RNN就是我们的LSTM。由于LSTM有很多的变种，这里我们以最常见的LSTM为例讲述。LSTM的结构如下图：

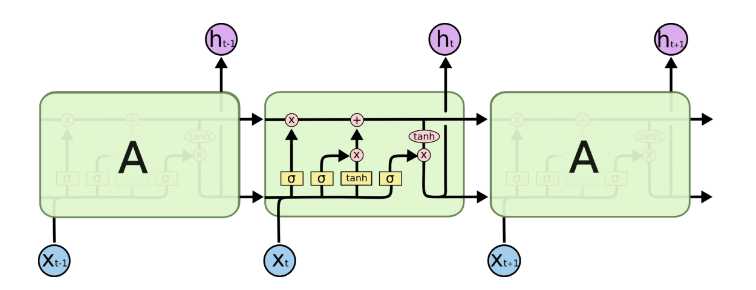
　　　　可以看到LSTM的结构要比RNN的复杂的多，真佩服牛人们怎么想出来这样的结构，然后这样居然就可以解决RNN梯度消失的问题？由于LSTM怎么可以解决梯度消失是一个比较难讲的问题，我也不是很熟悉，这里就不多说，重点回到LSTM的模型本身。

?2. LSTM模型结构剖析

　　　　上面我们给出了LSTM的模型结构，下面我们就一点点的剖析LSTM模型在每个序列索引位置t时刻的内部结构。
　　　　从上图中可以看出，在每个序列索引位置t时刻向前传播的除了和RNN一样的隐藏状态\\(h^(t)\\)，还多了另一个隐藏状态，如图中上面的长横线。这个隐藏状态我们一般称为细胞状态(Cell State)，记为\\(C^(t)\\)。如下图所示：

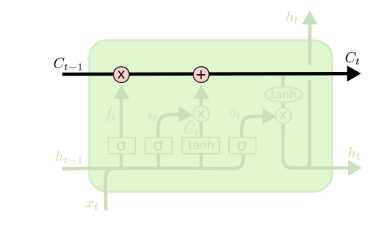
　　　　除了细胞状态，LSTM图中还有了很多奇怪的结构，这些结构一般称之为门控结构(Gate)。LSTM在在每个序列索引位置t的门一般包括遗忘门，输入门和输出门三种。下面我们就来研究上图中LSTM的遗忘门，输入门和输出门以及细胞状态。

?2.1 LSTM之遗忘门

　　　　遗忘门（forget gate）顾名思义，是控制是否遗忘的，在LSTM中即以一定的概率控制是否遗忘上一层的隐藏细胞状态。遗忘门子结构如下图所示：

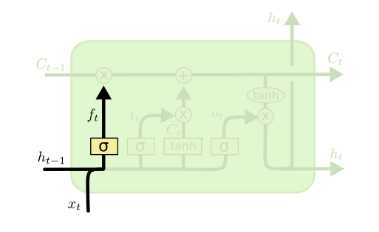
　　　　图中输入的有上一序列的隐藏状态\\(h^(t-1)\\)和本序列数据\\(x^(t)\\)，通过一个激活函数，一般是sigmoid，得到遗忘门的输出\\(f^(t)\\)。由于sigmoid的输出\\(f^(t)\\)在[0,1]之间，因此这里的输出f^(t)代表了遗忘上一层隐藏细胞状态的概率。用数学表达式即为：\\[f^(t) = \\sigma(W_fh^(t-1) +?U_fx^(t) + b_f)\\]
　　　　其中\\(W_f, U_f, b_f\\)为线性关系的系数和偏倚，和RNN中的类似。\\(\\sigma\\)为sigmoid激活函数。

2.2 LSTM之输入门

　　　　输入门（input gate）负责处理当前序列位置的输入，它的子结构如下图：

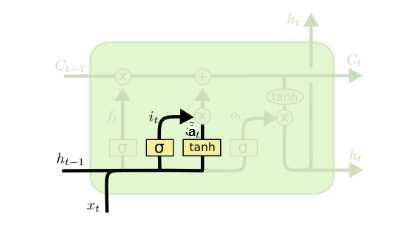
　　　　从图中可以看到输入门由两部分组成，第一部分使用了sigmoid激活函数，输出为\\(i^(t)\\),第二部分使用了tanh激活函数，输出为\\(a^(t)\\), 两者的结果后面会相乘再去更新细胞状态。用数学表达式即为：\\[i^(t) = \\sigma(W_ih^(t-1) +?U_ix^(t) + b_i)\\]\\[a^(t) =tanh(W_ah^(t-1) +?U_ax^(t) + b_a)\\]
　　　　其中\\(W_i, U_i, b_i, W_a, U_a, b_a,\\)为线性关系的系数和偏倚，和RNN中的类似。\\(\\sigma\\)为sigmoid激活函数。

2.3 LSTM之细胞状态更新

　　　　在研究LSTM输出门之前，我们要先看看LSTM之细胞状态。前面的遗忘门和输入门的结果都会作用于细胞状态\\(C^(t)\\)。我们来看看从细胞状态\\(C^(t-1)\\)如何得到\\(C^(t)\\)。如下图所示：

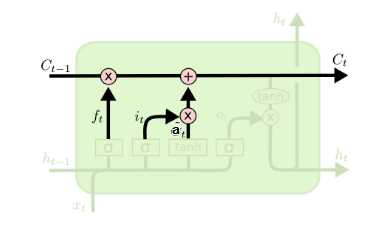
　　　　细胞状态\\(C^(t)\\)由两部分组成，第一部分是\\(C^(t-1)\\)和遗忘门输出\\(f^(t)\\)的乘积，第二部分是输入门的\\(i^(t)\\)和\\(a^(t)\\)的乘积，即：\\[C^(t) = C^(t-1) \\odot?f^(t) +?i^(t)?\\odot?a^(t)\\]
　　　　其中，\\(\\odot\\)为Hadamard积，在DNN中也用到过。

2.4 LSTM之输出门

　　　　有了新的隐藏细胞状态\\(C^(t)\\)，我们就可以来看输出门了，子结构如下：

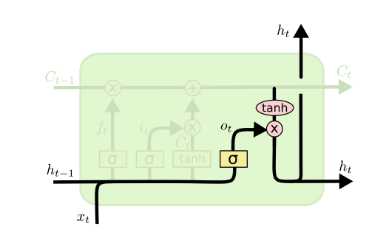
　　　　从图中可以看出，隐藏状态\\(h^(t)\\)的更新由两部分组成，第一部分是\\(o^(t)\\), 它由上一序列的隐藏状态\\(h^(t-1)\\)和本序列数据\\(x^(t)\\)，以及激活函数sigmoid得到，第二部分由隐藏状态\\(C^(t)\\)和tanh激活函数组成, 即：\\[o^(t) = \\sigma(W_oh^(t-1) +?U_ox^(t) + b_o)\\]\\[h^(t) = o^(t) \\odot tanh(C^(t))\\]
　　　　通过本节的剖析，相信大家对于LSTM的模型结构已经有了解了。当然，有些LSTM的结构和上面的LSTM图稍有不同，但是原理是完全一样的。

3. LSTM前向传播算法

　　　　现在我们来总结下LSTM前向传播算法。LSTM模型有两个隐藏状态\\(h^(t), C^(t)\\)，模型参数几乎是RNN的4倍，因为现在多了\\(W_f, U_f, b_f, W_a, U_a, b_a, W_i, U_i, b_i, W_o, U_o, b_o\\)这些参数。
　　　　前向传播过程在每个序列索引位置的过程为：
　　　　1）更新遗忘门输出：\\[f^(t) = \\sigma(W_fh^(t-1) +?U_fx^(t) + b_f)\\]
　　　　2）更新输入门两部分输出：\\[i^(t) = \\sigma(W_ih^(t-1) +?U_ix^(t) + b_i)\\]\\[a^(t) = tanh(W_ah^(t-1) +?U_ax^(t) + b_a)\\]
　　　　3）更新细胞状态：\\[C^(t) = C^(t-1) \\odot?f^(t) +?i^(t)?\\odot?a^(t)\\]
　　　　4）更新输出门输出：\\[o^(t) = \\sigma(W_oh^(t-1) +?U_ox^(t) + b_o)\\]\\[h^(t) = o^(t) \\odot tanh(C^(t))\\]
　　　　5）更新当前序列索引预测输出：\\[\\haty^(t) = \\sigma(Vh^(t) + c)\\]

4. ?LSTM反向传播算法推导关键点

　　　　有了LSTM前向传播算法，推导反向传播算法就很容易了， 思路和RNN的反向传播算法思路一致，也是通过梯度下降法迭代更新我们所有的参数，关键点在于计算所有参数基于损失函数的偏导数。
　　　　在RNN中，为了反向传播误差，我们通过隐藏状态\\(h^(t)\\)的梯度\\(\\delta^(t)\\)一步步向前传播。在LSTM这里也类似。只不过我们这里有两个隐藏状态\\(h^(t)\\)和\\(C^(t)\\)。这里我们定义两个\\(\\delta\\)，即：\\[\\delta_h^(t) = \\frac\\partial L\\partial h^(t)\\]\\[\\delta_C^(t) = \\frac\\partial L\\partial?C^(t)\\]
　　　　为了便于推导，我们将损失函数\\(L(t)\\)分成两块，一块是时刻\\(t\\)位置的损失\\(l(t)\\)，另一块是时刻\\(t\\)之后损失\\(L(t+1)\\)，即：\\[L(t) = \\begincases l(t) + L(t+1) &amp; \\textif \\, t <;?\\tau \\\\ l(t) &amp; \\textif \\, t = \\tau\\endcases\\]　　　　
　　　　而在最后的序列索引位置\\(\\tau\\)的\\(\\delta_h^(\\tau)\\)和?$\\delta_C^(\\tau) \\(为：\\)\\(\\delta_h^(\\tau) =(\\frac\\partial O^(\\tau)\\partial?h^(\\tau))^T\\frac\\partial L^(\\tau)\\partial O^(\\tau)? = V^T(\\haty^(\\tau) - y^(\\tau))\\)\\[$\\delta_C^(\\tau) =(\\frac\\partial h^(\\tau)\\partial?C^(\\tau))^T\\frac\\partial L^(\\tau)\\partial h^(\\tau)? = \\delta_h^(\\tau) \\odot ?o^(\\tau) \\odot (1 - tanh^2(C^(\\tau)))\\]
　　　　接着我们由\\(\\delta_C^(t+1),\\delta_h^(t+1)\\)反向推导\\(\\delta_h^(t), \\delta_C^(t)\\)。
　　　　\\(\\delta_h^(t)\\)的梯度由本层t时刻的输出梯度误差和大于t时刻的误差两部分决定，即：\\[? \\delta_h^(t) =\\frac\\partial L\\partial?h^(t)? =\\frac\\partial l(t)\\partial?h^(t) + (?\\frac\\partial h^(t+1)\\partial?h^(t))^T\\frac\\partial L(t+1)\\partial?h^(t+1)? = V^T(\\haty^(t) - y^(t)) + (\\frac\\partial h^(t+1)\\partial?h^(t))^T\\delta_h^(t+1) \\]
　　　　整个LSTM反向传播的难点就在于$?\\frac\\partial h^(t+1)\\partial?h^(t)\\(这部分的计算。仔细观察，由于\\)h^(t) = o^(t) \\odot tanh(C^(t))\\(, 在第一项\\)o^(t)\\(中，包含一个\\)h\\(的递推关系，第二项\\)tanh(C^(t))\\(就复杂了，\\)tanh\\(函数里面又可以表示成：\\)\\(C^(t) = C^(t-1) \\odot?f^(t) +?i^(t)?\\odot?a^(t)\\)$
　　　　\\(tanh\\)函数的第一项中，\\(f^(t)?\\)包含一个\\(h\\)的递推关系，在\\(tanh\\)函数的第二项中，\\(i^(t)\\)和\\(a^(t)\\)都包含\\(h\\)的递推关系，因此，最终$?\\frac\\partial h^(t+1)\\partial?h^(t)$这部分的计算结果由四部分组成。即：
\\[\\Delta C = o^(t+1) \\odot [1-tanh^2(C^(t+1))]\\]
\\[\\frac\\partial h^(t+1)\\partial h^(t) = W_o^T [o^(t+1) \\odot (1-o^(t+1)) \\odot tanh(C^(t+1))] +? W_f^T [\\Delta C? \\odot f^(t+1) \\odot (1-f^(t+1)) \\odot C^(t)] + W_a^T \\ \\Delta C? \\odot i^(t+1) \\odot [1-(a^(t+1))^2] \\? + W_i^T [\\Delta C? \\odot a^(t+1) \\odot? i^(t+1)? \\odot (1-i^(t+1))]\\]
　　　　而\\(\\delta_C^(t)\\)的反向梯度误差由前一层\\(\\delta_C^(t+1)\\)的梯度误差和本层的从\\(h^(t)\\)传回来的梯度误差两部分组成，即：\\[\\delta_C^(t) =(\\frac\\partial ?C^(t+1)\\partial?C^(t)?)^T\\frac\\partial L\\partial C^(t+1) + (\\frac\\partial h^(t)\\partial C^(t)?)^T\\frac\\partial L\\partial h^(t)= (\\frac\\partial ?C^(t+1)\\partial?C^(t)?)^T\\delta_C^(t+1) + \\delta_h^(t) \\odot ?o^(t) \\odot (1 - tanh^2(C^(t))) = \\delta_C^(t+1) \\odot f^(t+1) + \\delta_h^(t) \\odot ?o^(t) \\odot (1 - tanh^2(C^(t)))\\]
　　　　有了\\(\\delta_h^(t)\\)和\\(\\delta_C^(t)\\)， 计算这一大堆参数的梯度就很容易了，这里只给出\\(W_f\\)的梯度计算过程，其他的\\(U_f, b_f, W_a, U_a, b_a, W_i, U_i, b_i, W_o, U_o, b_o，V, c\\)的梯度大家只要照搬就可以了。\\[\\frac\\partial L\\partial W_f =\\sum\\limits_t=1^\\tau [\\delta_C^(t) \\odot?C^(t-1) \\odot f^(t)\\odot(1-f^(t))] (h^(t-1))^T\\]

5. LSTM小结

　　　　LSTM虽然结构复杂，但是只要理顺了里面的各个部分和之间的关系，进而理解前向反向传播算法是不难的。当然实际应用中LSTM的难点不在前向反向传播算法，这些有算法库帮你搞定，模型结构和一大堆参数的调参才是让人头痛的问题。不过，理解LSTM模型结构仍然是高效使用的前提。
（欢迎转载，转载请注明出处。欢迎沟通交流： [e-mail]）

参考资料：

1）?Neural Networks and Deep Learning?by?By Michael Nielsen
2）?Deep Learning, book by Ian Goodfellow, Yoshua Bengio, and Aaron Courville
3）?UFLDL Tutorial
4）Understanding-LSTMs