二叉树三种深度遍历方法和实现

Posted 2022-04-19 sinlyfly

三种遍历的基本思想

先序遍历：根节点 -> 左子树 -> 右子树

中序遍历：左子树 -> 根节点 -> 右子树

后序遍历：左子树 -> 右子树 -> 根节点

如，以下二叉树遍历：

 

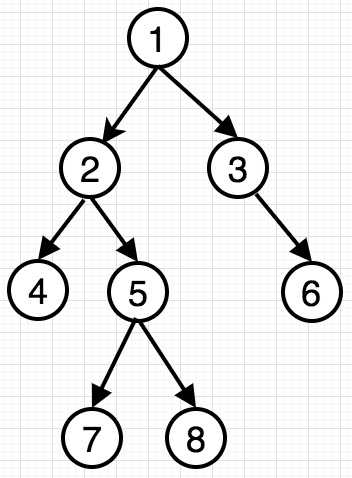
先序遍历结果：1 2 4 5 7 8 3 6

中序遍历结果：4 2 7 5 8 1 3 6

后序遍历结果：4 7 8 5 2 6 3 1

 

二叉树基本结构

1 function TreeNode(val) 
2 
3 　　this.val = val;
4 
5 　　this.left = this.right = null;
6 
7 

一、先序遍历

• 递归实现：先处理当前节点，然后递归处理左子节点，最后递归处理右子节点

1 function preVisitRecursive(root) 
2     if(root) 
3         console.log(root.val);       //处理当前节点
4         preVisit(root.left);         //递归处理左子节点
5         preVisit(root.right);        //递归处理右子节点
6     
7 

• 非递归实现：使用栈（后进先出）来保存返回需要处理的节点

 1 function preVisit(root) 
 2     let curNode = root, treeNode = [];
 3     while(curNode !== null  || treeNode.length > 0) 
 4         if(curNode!== null) 
 5             console.log(curNode.val);      //处理当前节点
 6             treeNode.push(curNode);        
 7             curNode = curNode.left;        //指向左子节点做同样处理
 8          else 
 9             curNode = treeNode.pop();      //栈顶元素出栈
10             curNode = curNode.right;       //指向右子节点
11         
12     
13 

二、中序遍历

• 递归实现：先递归处理左子节点，再处理当前节点，最后递归处理右子节点

1 function midVisitRecursive(root) 
2     if(root) 
3         preVisit(root.left);         //递归处理左子节点
4         console.log(root.val);       //处理当前节点    
5         preVisit(root.right);        //递归处理右子节点
6     
7 

• 非递归实现：使用栈（后进先出）来保存返回需要处理的节点

 1 function midVisit(root) 
 2     let curNode = root, treeNode = [];
 3     while(curNode !== null  || treeNode.length > 0) 
 4         if(curNode!== null) 
 5             treeNode.push(curNode);        
 6             curNode = curNode.left;        //指向左子节点做同样处理
 7          else 
 8             curNode = treeNode.pop();      //栈顶元素出栈
 9             console.log(curNode.val);      //处理当前节点
10             curNode = curNode.right;       //指向右子节点
11         
12     
13 

三、后序遍历

• 递归实现：先递归处理左子节点，然后递归处理右子节点，最后处理当前节点

1 function postVisitRecursive(root) 
2     if(root) 
3         preVisit(root.left);         //递归处理左子节点    
4         preVisit(root.right);        //递归处理右子节点
5         console.log(root.val);       //处理当前节点
6     
7 

• 非递归实现：需要保证左子节点和右子节点都被访问 且 右子节点在左子节点访问之后 才能访问根节点

1）对于任一结点P，将其入栈，然后沿其左子树一直往下搜索，直到搜索到没有左孩子的结点，此时该结点出现在栈顶，但是此时不能将其出栈并访问，因为其右孩子还未被访问。

    所以接下来按照相同的规则对其右子树进行相同的处理，当访问完其右孩子时，该结点又出现在栈顶，此时可以将其出栈并访问。这样就保证了正确的访问顺序。

    可以看出，在这个过程中，每个结点都两次出现在栈顶，只有在第二次出现在栈顶时，才能访问它。因此需要多设置一个变量标识该结点是否是第一次出现在栈顶。

 1 function postVisit(root) 
 2     let curNode = root, treeNode = [];
 3     while(curNode !== null || treeNode.length > 0) 
 4     
 5             if(curNode !== null)
 6             
 7                 curNode.isFirst = true;
 8                 treeNode.push(curNode);  //当前节点入栈
 9                 curNode = curNode.left;  //指向left，进行步骤1处理
10              else 
11                 curNode = treeNode.pop();  //指向栈顶元素
12                 if(curNode.isFirst)       //表示第一次出栈顶
13                     curNode.isFirst = false;
14                     treeNode.push(curNode);
15                     curNode =curNode.right
16                  else                  //第二次出栈顶
17                     console.log(curNode.val);
18                     curNode = null;     //进行步骤2
19                 
20             
21     
22         
23 

View Code

觉得不错的另外的实现

 

2）要保证左子节点和右子节点都被访问之后才能访问根节点。对于任一节点P，先将其入栈。如果其不存在左子节点和右子节点，可直接访问；亦或其存在左子节点或右子节点，且其左子节点和右子节点已被访问过，则可直接访问该节点；其他情况下，则将其右子节点和左子节点依次入栈，这样保证了出栈时左子节点在右子节点之前被访问，根节点在子节点之后被访问

 1 function postVisit(root) 
 2     let treeNode = [], 
 3             curNode,             //当前节点
 4             pre = null;          //上一次访问的节点
 5     treeNode.push(root);
 6     while(treeNode.length > 0) 
 7         curNode = treeNode[treeNode.length - 1];
 8         // 若当前节点没有左子节点和右子节点或者孩子节点均被访问过
 9         if((curNode.left === null && curNode.right === null) || (pre && (pre === curNode.left || pre === curNode.right))) 
10             console.log(curNode.val);
11             treeNode.pop();
12             pre = curNode;
13          else 
14             if(curNode.right) 
15                 treeNode.push(curNode.right);
16             
17             if(curNode.left) 
18                 treeNode.push(curNode.left);
19             
20         
21     
22 

View Code

 四、二叉树与数组相结合

从二叉搜索树(BST)中找出是否存在两个节点的和等于某个值k

 1 /**
 2  * @param TreeNode root
 3  * @param number k
 4  * @return boolean
 5  */
 6 var findTarget = function(root, k) 
 7   let treeNode = [], numsArr = [], curNode = root;
 8   while(curNode !== null || treeNode.length > 0) 
 9     if(curNode !== null) 
10       treeNode.push(curNode);
11       curNode = curNode.left;
12      else 
13       curNode = treeNode.pop();
14       numsArr.push(curNode.val);
15       curNode = curNode.right;
16     
17   
18   let m = 0, n = numsArr.length - 1, sum = numsArr[m] + numsArr[n];
19   while(m < n) 
20     if(sum === k) return true;
21     sum < k ? m++ : n--;
22     sum = numsArr[m] + numsArr[n];
23   
24   return false
25 ;