(算法)压缩算法(哈夫曼树)

Posted 2022-04-13 fangdongdemao

哈夫曼树(赫夫曼树/霍夫曼树 /最优树)

若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树

应用场景文件压缩,又叫压缩算法

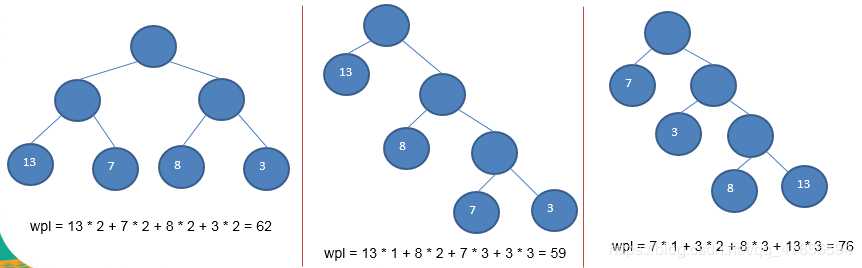
现在有3课二叉树,都有四个节点,分别带权13,7,8,3

一段字符串中计算每一个字符重复的次数

let a = 'ab cbdal abc'
console.log(a.split('').reduce((acc, val) => 
    acc[val] = (acc[val] || 0) + 1
    return acc
, ))
//升级版
const getFreqs = text => [...text]
    .reduce((acc, val) => (acc[val]
            ? ...acc, [val]: acc[val] + 1
            : ...acc, [val]: 1
    ), )
console.log(getFreqs('abc abx'))

//第二种
const cal = str => 
    let map = 
    let i = 0
    while (str[i]) 
        //首先添加str[i]的属性,因为刚开始没值,所以复制为1
        map[str[i]] ? map[str[i]]++ : map[str[i]] = 1
        i++
    
    return map

console.log(cal('abc ab cc '))

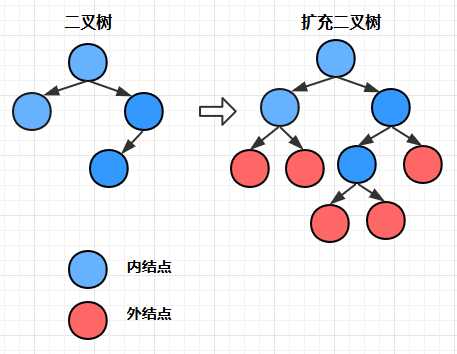
扩充二叉树

对于一颗已有的二叉树,如果我们为他添加一系列新结点,使得他原有的所有结点的度都为2,那么我们得到了一颗扩充二叉树:

其中原有的结点叫做内结点(非叶子结点),新增加的结点叫做叶结点(叶子结点)

外结点数=内结点数+1

总结点数=2*外结点数-1

那什么结点的度?

• 结点的度指的是二叉树结点的分支数目,如果某个节点没有孩子结点,即使没有分支,那么他的度是0,如果有一个孩子的结点,那么他的度数是1,如果既有左孩子也有右孩子,那么这个结点的度是2

赫夫曼树的外结点和内结点

性质区别: 外结点是携带了关键数据的节点,二内部节点没有携带这种数据,只作为导向最终的外结点所走的路径而使用

正因如此,我们的关注点最后是落在赫夫曼树的外结点上,而不是內结点

带权路径长度WPL

如果一个数据结点搜索频率越高,就让他分布在离根结点越近的地方,也就是根结点走到该节点经过的路径长度越短

频率是个细化的量,这里我们使用一个更加标准的一个词描述他---"权值"

**我们为扩充二叉树的外结点(叶子结点)定义两条属性:权值(W)和路径长度(L),同时规定带权路径长度(WPL) 为扩充二叉树的外结点的权值和路径长度的乘积之和(只是外结点)

外结点的带权路径长度（WPL） = T的根到该节点的路径长度 *? 该节点的权值

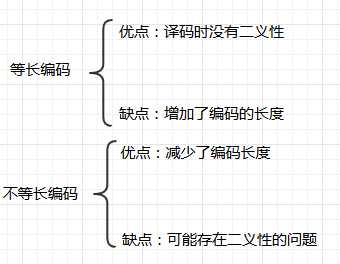
等长编码和不等长编码

前缀编码

要设计长短不等的编码,则必须保证:任意一个字符的编码都不是另一个字符的编码的前缀,这种编码叫做前缀编码

赫夫曼编码

赫夫曼编码就是一种前缀编码,他能解决不等长的译码问题,通过他,我们能尽可能减少编码的长度,同时还能过避免二义性,实现正确编码

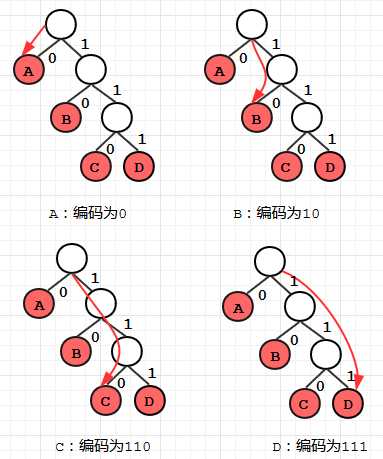
赫夫曼树的构造

赫夫曼树是一棵满二叉树,树中只有两种类型的结点,即叶子节点和度为2的结点,所有树中任意结点的左子树和右子树同时存在

对字符集合按照字符频率进行升序排序,并构建一颗空树

若字符频率不大于根节点频率，则字符作为根节点的左兄弟，形成一个新的根节点，频率值为左、右子节点之和；

若字符频率大于根结点频率,则字符作为根结点的右兄弟,形成一个新的根结点,频率值为左右子节点之和

举例:

1. 做4个叶节点,分别以2,4,5,7为权

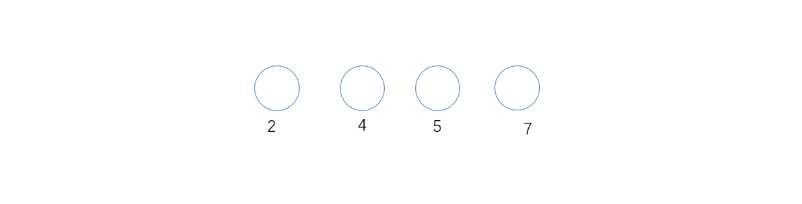
2. 从所有入度为0的结点中,最小的两个节点为2和4,则组成6这个分支

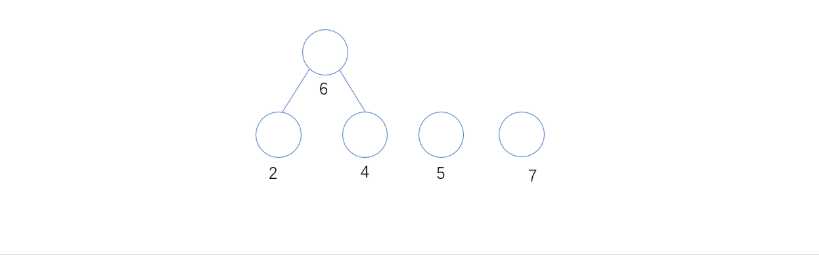
3. 从所有入度为0的结点中，最小的两个结点为5和6，则组成11这个分支节点

4. 从所有入度为0的结点中，最小的两个结点为7和11，则组成18这个分支节点，此时只有一个入度为0的顶点为18，组成了下图的二叉树，完成

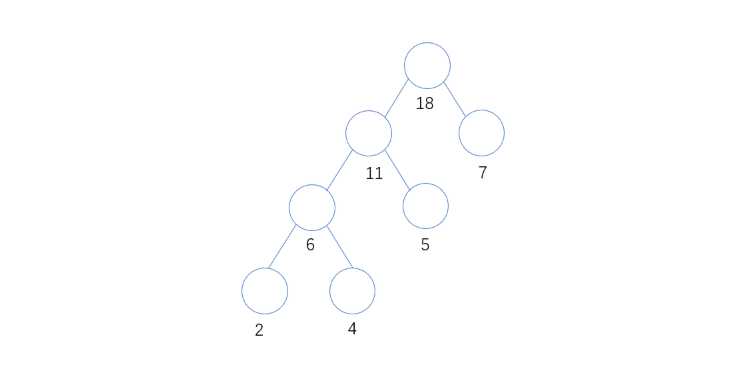
对字符集合按照频率进行排序,这里使用插入排序

//字符集合为
const contentArr = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J']
//对应的频率
const valueArr = [5, 3, 4, 0, 2, 1, 8, 6, 9, 7]
//使用插入排序
const insertionSort = (valueArr, contentArr) => 
    let tmpValue, tmpContent
    for (let i = 1; i < valueArr.length; i++) 
        tmpValue = valueArr[i]
        tmpContent = contentArr[i]
        while (i > 0 && tmpValue < valueArr[i - 1]) 
            valueArr[i] = valueArr[i - 1]
            contentArr[i] = contentArr[i - 1]
            i--
        
        valueArr[i] = tmpValue
        contentArr[i] = tmpContent
    
    return contentArr

console.log(insertionSort(valueArr, contentArr))

我自己写的垃圾排序(通过排序的索引对原数组进行重新排序)
let arr = valueArr.slice().sort((a, b) => a - b)
arr.reduce((acc, val) => 
    acc.push(contentArr[valueArr.indexOf(val)])
    return acc
, [])

完整步骤前端版

//把字符串重复的转化成重复次数的对象

const getFreqs = text => [...text]
  .reduce((acc, letter) => (acc[letter]
    ?  ...acc, [letter]: acc[letter] + 1 
    :  ...acc, [letter]: 1 
  ), );
//console.log(getFreqs('abc ab'))
// a: 2, b: 2, c: 1, ' ': 1 

//把对象转成一个二维数组
const toPairs = freqs => Object.keys(freqs)
  .map(letter => [letter, freqs[letter]]);
//给二维数组排序
const sortPairs = pairs => [...pairs]
  .sort(([, leftFreq], [, rightFreq]) => leftFreq - rightFreq);
//递归创建树
const getTree = pairs => (pairs.length < 2
  ? pairs[0]
  : getTree(sortPairs([
    [pairs.slice(0, 2), pairs[0][1] + pairs[1][1]],
    ...pairs.slice(2)]))
);
//递归编码
const getCodes = (tree, pfx = '') => (tree[0] instanceof Array
  ? Object.assign(
    getCodes(tree[0][0], `$pfx0`),
    getCodes(tree[0][1], `$pfx1`),
  )
  :  [tree[0]]: pfx );

export default (text) => 
  const freqs = getFreqs(text);
  const freqPairs = toPairs(freqs);
  const sortedFreqPairs = sortPairs(freqPairs);
  const tree = getTree(sortedFreqPairs);
  const codes = getCodes(tree);

  return [...text]
    .map(letter => codes[letter])
    .join('');
;

第二版

//字符串转对象
const freqs = text => [...text].reduce((acc, val) => (
        (acc[val] ? acc[val] = acc[val] + 1 : acc[val] = 1), acc)
    , )
console.log(freqs('abc ab '))
// a: 1, b: 1, c: 1, ' ': 1 
//把对象转成二维数组
const topaire = freqs => Object.keys(freqs).map(val => [val, freqs[val]])
console.log(topaire(freqs('abc ab ')))
//[ [ 'a', 1 ], [ 'b', 1 ], [ 'c', 1 ], [ ' ', 1 ] ]
//二维数组排序
const sortps = pairs => pairs.sort((a, b) => a[1] - b[1])
console.log(sortps(topaire(freqs('abc ab '))))
//[ [ 'c', 1 ], [ 'a', 2 ], [ 'b', 2 ], [ ' ', 2 ] ]
//构建树
const tree = ps => 
    if (ps.length < 2) 
        return ps[0]
    
    //拿到最小的两个,然后求和,然后把剩下的合并起来,进行递归创建出树
    return tree(sortps([[ps.slice(0, 2), ps[0][1] + ps[1][1]]].concat(ps.slice(2))))

console.log(tree(sortps(topaire(freqs('abc ab ')))))
//编码
const codes = (tree, pfx = '') => 
    if (tree[0] instanceof Array) 
        return Object.assign(codes(tree[0][0], pfx + '0'), codes(tree[0][1], pfx + '1'))
    
    return ([tree[0]]: pfx)

console.log(codes(tree(sortps(topaire(freqs('abc ab '))))))
//将字符串编码
const encode = str => 
    let output = '编码'
    let a = c: '00', a: '01', b: '10', ' ': '11'
    for (const item in str) 
        output = output + a[str[item]]
    
    return output

console.log(encode('abc ab '))
//反码
function decode(str, dictionary) 
    let arr = []
    for (let i = 0; i < Math.floor(str.length / 2); i++) 
        arr.push(str.substr(i, 2))
    
    let output = '反码: '
    const lettersArr = Object.keys(dictionary)
    const valuesArr = Object.values(dictionary)
    for (let i = 0; i < arr.length; i++) 
        for (let j = 0; j < valuesArr.length; j++) 
            if (arr[i] == valuesArr[j]) 
                output += lettersArr[j]
            
        
    
    return output


console.log(decode('01100011011011', c: '00', a: '01', b: '10', ' ': '11'))

压缩版

function dictionary(text) 
  const freqs = text => [...text].reduce((fs, c) => (fs[c] ? (fs[c] = fs[c] + 1, fs) : (fs[c] = 1, fs)), );
  const topairs = freqs => Object.keys(freqs).map(c => [c, freqs[c]]);
  const sortps = pairs  => pairs.sort((a, b) => a[1] - b[1]);
  const tree = ps => (ps.length < 2 ? ps[0] : tree(sortps([[ps.slice(0, 2), ps[0][1] + ps[1][1]]].concat(ps.slice(2)))));
  const codes = (tree, pfx = '')  => (tree[0] instanceof Array ? Object.assign(codes(tree[0][0], pfx + '0'), codes(tree[0][1], pfx + '1')) :  [tree[0]]: pfx );
  return codes(tree(sortps(topairs(freqs(text)))));

待续...