二分法之通用模板

Posted 2022-04-13 fromzore

在这里我们一共有两个模板

模板1

我们将区间[l,r]划分为[l,mid]和[mid+1,r]时，其更新操作是r=mid或者l=mid+1;计算mid时不用加一。

int searchRange(vector<int>& nums, int target) 
        int l=0,r=nums.size()-1;
        while(l<r)
            int mid=l+r>>1;
            if(check(mid))r=mid;
            else l=mid+1;
        
    return l;

模板2

我们将区间[l,r]划分成[l,mid-1]和[mid,r]时，更新操作是r=mid-1或者l=mid；这时为了防止死循环，计算mid时需要+1。因为普通的整型计算是向下取整的+1，相当于四舍五入。

int searchRange(vector<int>& nums, int target) 
        int l=0,r=nums.size()-1;
        while(l<r)
            int mid=l+r+1>>1;
            if(check(mid))l=mid;
            else r=mid-1;
        
    return l;

这两个模板都可以找到想要我们找到的target。举个例子如下图我们想要找到9

 

 首先使用模板一

int searchRange(vector<int>& nums, int target) 
        int l=0,r=nums.size()-1;
        while(l<r)
            int mid=l+r>>1;
            if(nums[mid]>=target)r=mid;
            else l=mid+1;
        
    return l;

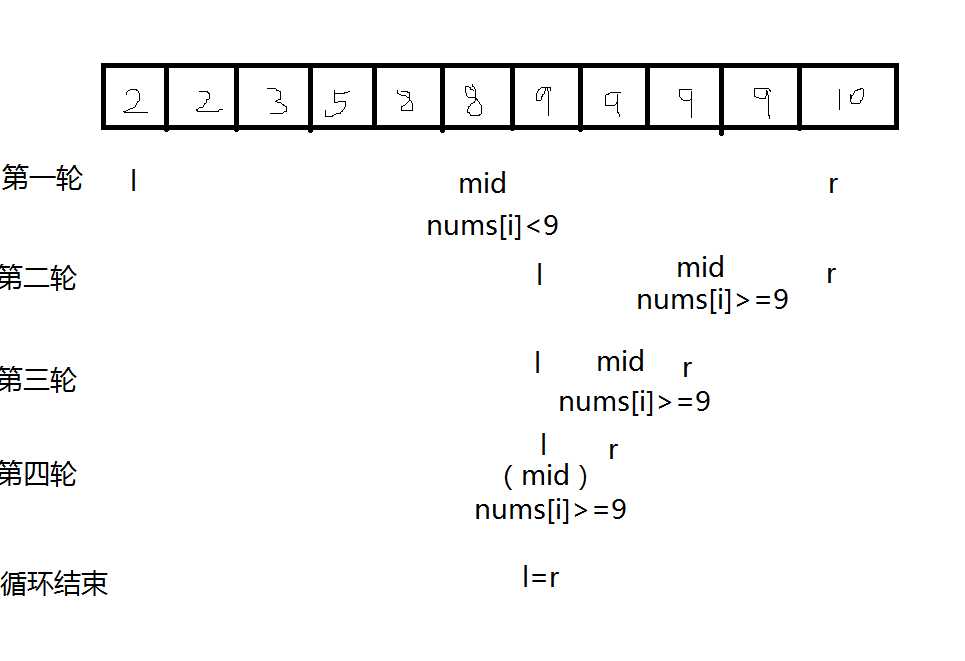
这样我们可以看到，模板一找到的最左边的等于target的数。

因为我们总是完全抛弃左边，右边抛弃除nums[mid]的数所以我们选择check函数为nums[mid]>=target。当数组中有相同的元素的时候，如图所示，当数组中没有相同的元素的时候，当nums[r]==target时，nums[mid]<target,l会一步步向右缩直到l=r。

然后我们使用模板二

int searchRange(vector<int>& nums, int target) 
        int l=0,r=nums.size()-1;
        while(l<r)
            int mid=l+r+1>>1;
            if(nums[mid]<=target)l=mid;
            else r=mid-1;
        
    return l;

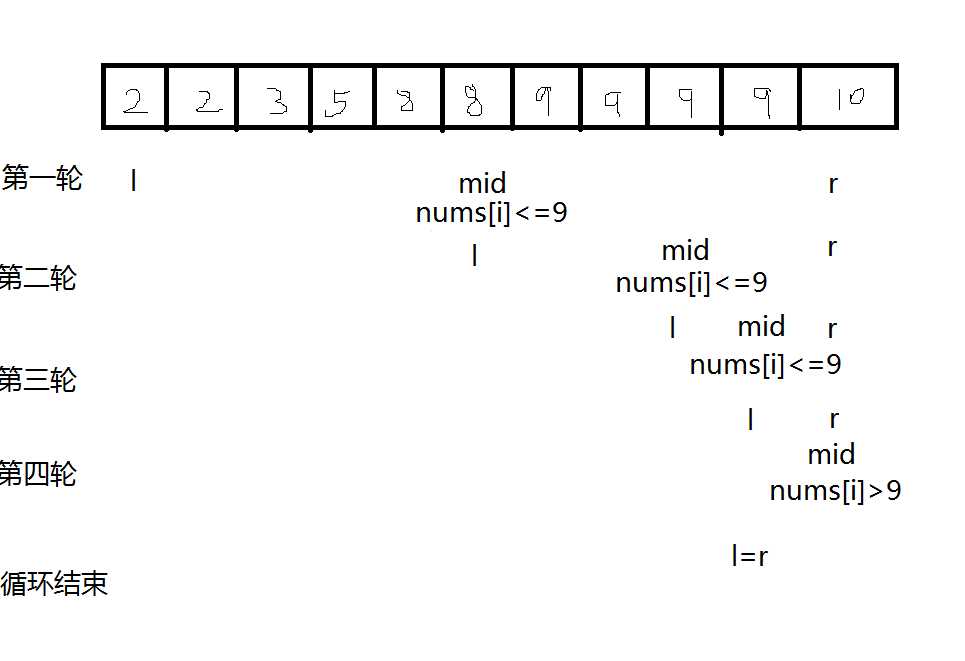
这样我们可以看到，模板一找到的最右边的等于target的数。

因为我们总是完全抛弃右边，左边抛弃除nums[mid]的数所以我们选择check函数为nums[mid]>=target。当数组中有相同的元素的时候，如图所示，当数组中没有相同的元素的时候，当nums[l]==target时，nums[mid]>target,r会一步步向右缩直到l=r。

所以对于没有相同元素的时候，使用两种模板都可以找到target。对于存在相同元素的时候，按照题意，进行判断是要找第一个为target还是最后一个为target的使用两种不同的模板。

这里有一道例题来帮助大家消化。

leetcode34. 在排序数组中查找元素的第一个和最后一个位置