梯度下降法及其实现

Posted 2022-04-08 sunnyside-bao

       本文将从一个下山的场景开始，先提出梯度下降算法的基本思想，进而从数学上解释梯度下降算法的原理，最后实现一个简单的梯度下降算法的实例！

梯度下降的场景假设

       梯度下降法的基本思想可以类比是一个下山的过程。可以假设一个场景：一个人上山旅游，天黑了，需要下山（到达山谷），这时候他看不清路，为了最快的下山，他可以找到所在位置最陡峭的地方，沿着高度下降的位置下山。

梯度下降

         我们有一个可微分函数，这个函数就像是这座大山，我们的目标就是找到这个函数的最小值，也就是下山。最快的下山方式就是找到这个山最陡峭的地方，然后下去，对应到函数里就是找到定点的梯度，然后朝着梯度相反的方向，就能让函数值下降的最快。

微分

看待微分的意义有两种不同的意义：

 

函数图像中，某点切线的斜率。

函数的变化率。

几个微分的例子：

 

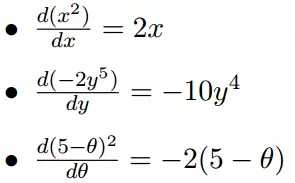
 上面的例子都是单变量的微分，下面举几个多变量的微分。

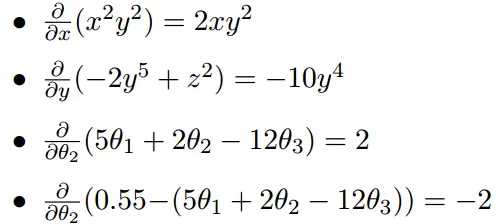
梯度

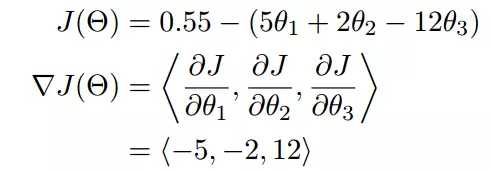
梯度是微积分中一个很重要的概念，之前提到过梯度的意义

• 在单变量的函数中，梯度其实就是函数的微分，代表着函数在某个给定点的切线的斜率
• 在多变量函数中，梯度是一个向量，向量有方向，梯度的方向就指出了函数在给定点的上升最快的方向

梯度下降算法的数学解释

上面我们花了大量的篇幅介绍梯度下降算法的基本思想和场景假设，以及梯度的概念和思想。下面我们就开始从数学上解释梯度下降算法的计算过程和思想！

 

梯度下降算法的实例

 下面我们将用python实现一个简单的梯度下降算法。场景是一个简单的线性回归的例子：假设现在我们有一系列的点，如下图所示

 

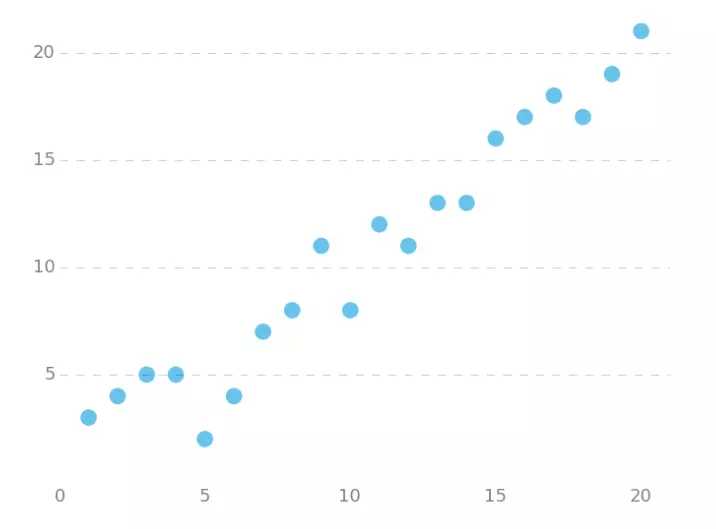
首先，我们需要定义一个代价函数，在此我们选用均方误差代价函数

 

此公示中

• m是数据集中点的个数
• ½是一个常量，这样是为了在求梯度的时候，二次方乘下来就和这里的½抵消了，自然就没有多余的常数系数，方便后续的计算，同时对结果不会有影响
• y 是数据集中每个点的真实y坐标的值

• h 是我们的预测函数，根据每一个输入x，根据Θ 计算得到预测的y值，即

   

   

我们可以根据代价函数看到，代价函数中的变量有两个，所以是一个多变量的梯度下降问题，求解出代价函数的梯度，也就是分别对两个变量进行微分

明确了代价函数和梯度，以及预测的函数形式。我们就可以开始编写代码了。但在这之前，需要说明一点，就是为了方便代码的编写，我们会将所有的公式都转换为矩阵的形式，python中计算矩阵是非常方便的，同时代码也会变得非常的简洁。

为了转换为矩阵的计算，我们观察到预测函数的形式

我们有两个变量，为了对这个公式进行矩阵化，我们可以给每一个点x增加一维，这一维的值固定为1，这一维将会乘到Θ0上。这样就方便我们统一矩阵化的计算

 

然后我们将代价函数和梯度转化为矩阵向量相乘的形式

coding time

首先，我们需要定义数据集和学习率

import numpy as np

# Size of the points dataset.
m = 20

# Points x-coordinate and dummy value (x0, x1).
X0 = np.ones((m, 1))
X1 = np.arange(1, m+1).reshape(m, 1)
X = np.hstack((X0, X1))

# Points y-coordinate
y = np.array([
    3, 4, 5, 5, 2, 4, 7, 8, 11, 8, 12,
    11, 13, 13, 16, 17, 18, 17, 19, 21
]).reshape(m, 1)

# The Learning Rate alpha.
alpha = 0.01

 

接下来我们以矩阵向量的形式定义代价函数和代价函数的梯度

def error_function(theta, X, y):
    ‘‘‘Error function J definition.‘‘‘
    diff = np.dot(X, theta) - y
    return (1./2*m) * np.dot(np.transpose(diff), diff)

def gradient_function(theta, X, y):
    ‘‘‘Gradient of the function J definition.‘‘‘
    diff = np.dot(X, theta) - y
    return (1./m) * np.dot(np.transpose(X), diff)

 

最后就是算法的核心部分，梯度下降迭代计算

def gradient_descent(X, y, alpha):
    ‘‘‘Perform gradient descent.‘‘‘
    theta = np.array([1, 1]).reshape(2, 1)
    gradient = gradient_function(theta, X, y)
    while not np.all(np.absolute(gradient) <= 1e-5):
        theta = theta - alpha * gradient
        gradient = gradient_function(theta, X, y)
    return theta

 

当梯度小于1e-5时，说明已经进入了比较平滑的状态，类似于山谷的状态，这时候再继续迭代效果也不大了，所以这个时候可以退出循环！

完整的代码如下

import numpy as np

# Size of the points dataset.
m = 20

# Points x-coordinate and dummy value (x0, x1).
X0 = np.ones((m, 1))
X1 = np.arange(1, m+1).reshape(m, 1)
X = np.hstack((X0, X1))

# Points y-coordinate
y = np.array([
    3, 4, 5, 5, 2, 4, 7, 8, 11, 8, 12,
    11, 13, 13, 16, 17, 18, 17, 19, 21
]).reshape(m, 1)

# The Learning Rate alpha.
alpha = 0.01

def error_function(theta, X, y):
    ‘‘‘Error function J definition.‘‘‘
    diff = np.dot(X, theta) - y
    return (1./2*m) * np.dot(np.transpose(diff), diff)

def gradient_function(theta, X, y):
    ‘‘‘Gradient of the function J definition.‘‘‘
    diff = np.dot(X, theta) - y
    return (1./m) * np.dot(np.transpose(X), diff)

def gradient_descent(X, y, alpha):
    ‘‘‘Perform gradient descent.‘‘‘
    theta = np.array([1, 1]).reshape(2, 1)
    gradient = gradient_function(theta, X, y)
    while not np.all(np.absolute(gradient) <= 1e-5):
        theta = theta - alpha * gradient
        gradient = gradient_function(theta, X, y)
    return theta

optimal = gradient_descent(X, y, alpha)
print(‘optimal:‘, optimal)
print(‘error function:‘, error_function(optimal, X, y)[0,0])

 

运行代码，计算得到的结果如下

 

所拟合出的直线如下

 

小结

至此，我们就基本介绍完了梯度下降法的基本思想和算法流程，并且用python实现了一个简单的梯度下降算法拟合直线的案例！
最后，我们回到文章开头所提出的场景假设:
这个下山的人实际上就代表了反向传播算法，下山的路径其实就代表着算法中一直在寻找的参数Θ，山上当前点的最陡峭的方向实际上就是代价函数在这一点的梯度方向，场景中观测最陡峭方向所用的工具就是微分 。在下一次观测之前的时间就是有我们算法中的学习率α所定义的。
可以看到场景假设和梯度下降算法很好的完成了对应！