转RM论坛 控制技术 PID控制中的I与D
Posted viggogao
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了转RM论坛 控制技术 PID控制中的I与D相关的知识,希望对你有一定的参考价值。
DJI RM论坛资料from:raymon DJI
第七课时 控制技术 PID控制中的I与D:
一、https://bbs.robomaster.com/thread-6194-1-1.html
二、https://bbs.robomaster.com/thread-6210-1-1.html
三、https://bbs.robomaster.com/thread-6212-1-1.html
以下为正文
一、第七课时 控制技术 PID控制中的I与D(一)
PID控制算法是《RoboMaster机器人基础》中最难的一个知识点,但是它对于机器人的控制来说却尤为重要。PID算法是机器人控制方面应用最广泛的算法,理解PID控制原理将在今后帮助大家更好地控制机器人。
这篇文章首先会为大家准备一个学习PID的“知识工具箱”。这个工具箱里包括了数学词汇,符号,和其他数学工具。
先让我们学习和回顾一些相关的数学概念。
1. 点(Point)
一个点是一个确切的位置。它没有大小或是维度。
<ignore_js_op>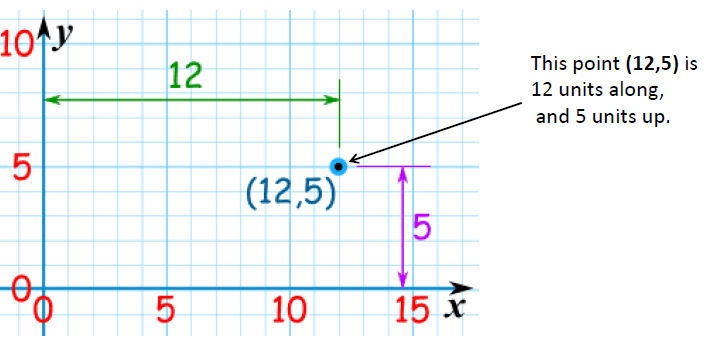

2. 无穷(Infinity)
“无穷”是指一个东西没有尽头,没有边界,无穷无尽。我们用“∞”这个符号来表示“无穷”。
3. 线(line)
一条线只有一个维度,它由无数个点相连组成。
<ignore_js_op>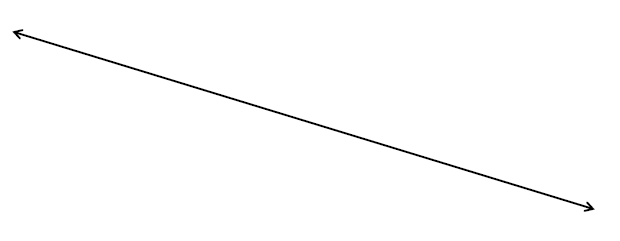

4. 切线(tangent line)
切线指的是一条刚好触碰到曲线上某一点的直线,更准确地说,当切线经过曲线上的某点(即切点)时,切线的方向与曲线上该点的方向是相同的。
<ignore_js_op>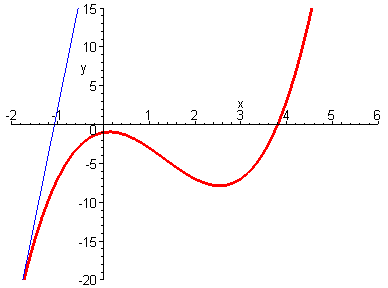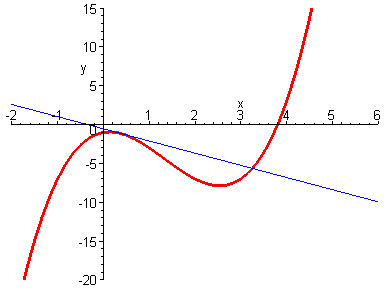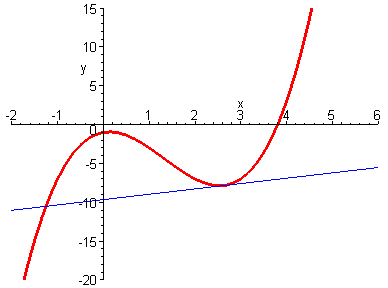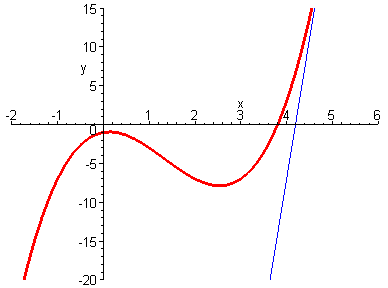

5. 变量(variable)
变量可以是一个符号,一个字母,一个单词去包含一个数值(如一个整数,一个实数)。下面公式中的x就是一个变量。
<ignore_js_op>

6. 函数(function)
一个函数将输入和输出以某种特殊关系联系起来。换句话说,一个函数再接受到输入以后,对输入的数据进行处理然后产生一个输出。在下面的一个函数里,f()是函数名,x是该函数的输入,x的平方是该函数的输出
<ignore_js_op>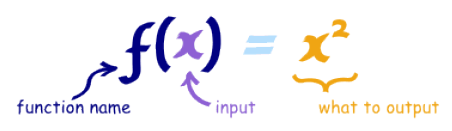

7. Delta (符号:Δ)
Δ表示数值之间的变化量。
举例:如果一个光传感器在采样时数值从75变成了50,我们说Delta为-25或是Δ=-25(50-75 = -25)。
8. 斜率(Slope/Gradient)
一条直线的斜率可以通过以下方式表示:
<ignore_js_op>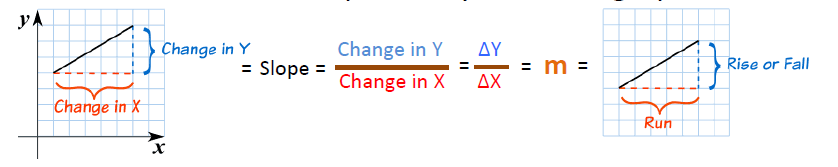
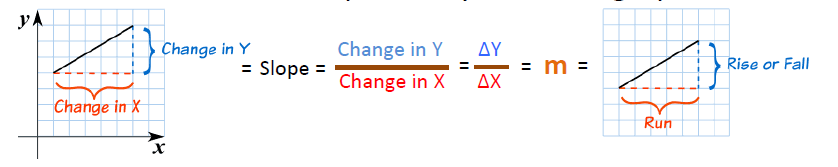
从上图中x,y的坐标系中可以看到如果我们将一个点从左下方移动到右上方,那么在x方向上的变化量为图中的“change in X”(ΔX),y方向的变化量为“change in Y”(ΔY),它们之间的比值“m”就是这条线的斜率。
下图是三个求直线斜率的例子,从左到右三根线的斜率分别为2,-2和0。
<ignore_js_op>

9. 求和(Summation)(符号:Σ)
Σ代表将所有的数值相加求和。
举个例子 ,1到9的Σ为“1+2+3+4+5+6+7+8+9=45”。
10. 直线的表达式
我们可以用变量来描述图中的任何直线,如下图中的直线可以被表示为 y=mx+b
<ignore_js_op>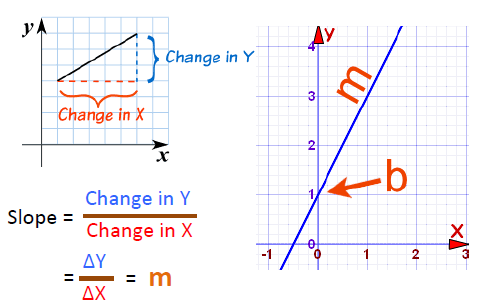

11. 微分
从书中我们已经知道PID中的三个大写英文字母分别对应的是P(Proportional 比例),I (Integral 积分)和D(Derivative 微分)。我们先通过一种通俗易懂的方式来学一学微分也就是PID中的D。
<ignore_js_op>

假设Jack 和 Jill两个小朋友要爬上一个小山丘去打水,我们将它们的运动位置拆分成水平距离(Distance)和高度(Height)。在山丘上的他们任意的一个位置都可以通过“距离”+ “高度”来进行表示。
<ignore_js_op>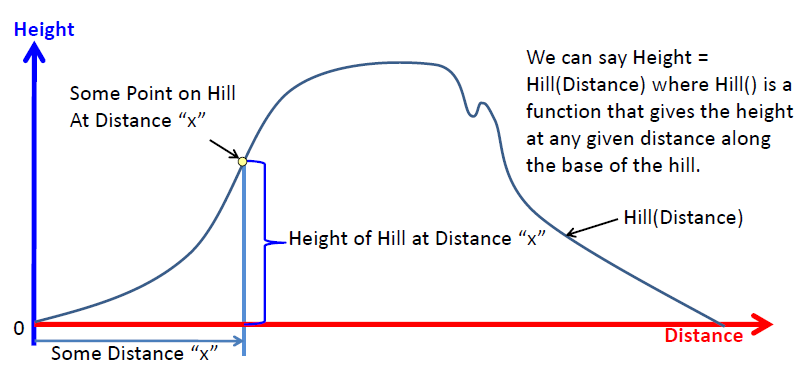

从上图中的小黄点可以看到,当行走的水平距离为x的时候,这个水平距离x会对应沙丘上的一个高度。因此,我们可以说山丘的“高度(Height)”是关于“距离(Distance)”的一个函数,该函数可以表达为 Height = Hill(Distance) , 其中Hill()是函数的名字,对于任何Distance的输入,都可以通过这个函数来输出一个相对应的高度(Height)。
更多关于微分和PID相关的其他内容请见下一篇文章 PID控制中的基本概念(二)。
二、第七课时 控制技术 PID控制中的I与D(二)
在上一篇文章中(PID中的I与D(一)),我们提到了一些关于学习PID控制中的微分控制与积分控制之前所需要掌握的一些数学知识,那么这篇文章会承接上一篇文章继续进行微分(D)的讲解。
接着上篇文章的Jack 和Jill爬山的例子,首先,我们可以将这个山丘的外形看作是一个函数图,在这个图上我们可以取到山丘上不同的位置点,如下图中的点A、点B、点C和点D。可以看到山丘上的每一个点或者说每一个位置都有它们所对应的斜率/坡度。
<ignore_js_op>

那我们应该通过什么方式来确定一个函数上的点所对应的斜率呢?大家都已经知道两个点可以确定一条直线,所以可以通过两个点确定一条直线的方式来估算其中一个点的斜率。过程如下:
如下图所示,我们设山坡上一点的水平距离(Distance)或横坐标为x(我们称点A),另一个点(点B)的水平距离要比点A多Δx,即它的横坐标为x+Δx,这两个点都有自己所对应的高度值(纵坐标),这两个纵坐标的值可以通过将横坐标的值带入上篇文章提到的Hill()函数来求得,即Hill(x)和Hill(x+Δx),现在有了两个点各自的横坐标和纵坐标,我们便可以粗略地求出穿过点B直线的斜率:<ignore_js_op>

当然,这仅仅是一种非常粗略的估算方法,为了更精确地估算出一个点上的斜率,我们需要见将Δx的值设置得非常非常小,这样这根直线就可以近似于一个点上的切线,方便我们更好估算在这个点上所对应斜率。
<ignore_js_op>

我们可以用上述算斜率的方法来对山丘函数上的每一个点进行斜率的计算,我们将这些斜率整理好并与每个水平距离一一对应,就可以得到每一个水平距离与它们所对应的斜率之间的关系。这个关系可以通过一个新的函数来表示,我们称这个数为HillSlope()。这个函数的意义在于,对于每一个水平距离的输入,它都可以输出一个在这个水平距离上所对应点的斜率。
我们将这个函数绘制成下方的第二幅图,这幅函数图描述的是每个水平位置与它们所对应的斜率的关系。
通过观察可以发现,当斜率为正数时,说明此处的坡度是向上的,斜率越大,向上的坡度越陡峭;当斜率为0时,说明该位置/点处在山坡的最平缓的地方,该处无任何坡度(如山丘的顶端);当斜率为负数时,说明此处的坡度是向下的,斜率越大,向下坡度越陡峭。
<ignore_js_op>

从第一幅图到第二图的整个过程就叫作微分。微分后的函数可以反映出原函数的每个点斜率的数值/变化速率。我们也称HillSlope()是Hill()的导函数。关于导函数和积分请参见下一篇文章 PID中的I与D(三)。
二、第七课时 控制技术 PID控制中的I与D(三)
接着上篇文章我们继续讨论,本篇文章主要讲解关于导函数,和积分的一些基础知识。
导函数:
导函数是一个表述函数上每个点斜率的函数,任何一个函数都会有对应的导函数,如上篇文章里的HillSlope()函数就是Hill()函数的导函数。利用在上篇文章里提到的用穿过两个相邻点的直线来估算斜率的方式(如下图所示),我们可以将一个导函数写成这种形式:
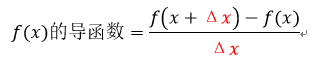
<ignore_js_op>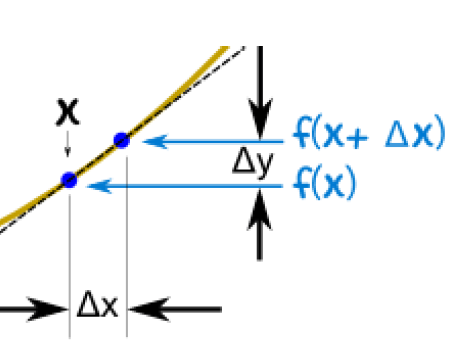

积分(Integral):
积分是微分的逆运算,我们可以对一个函数进行积分来求得它的积分函数。
如下图中的例子,下面图中的第一幅图描述的是自行车速度随时间变化的图像,从图像中可以看出,自行车一共行驶了5个小时,在第1个小时内自行车速度为5miles/hour, 在第2和第3个小时内,自行车的速度为10miles/hour, 第4个小时内的速度为15miles/hour,第5个小时内的速度为5miles/hr。如果我们想要知道在这5个小时内自行车行驶的总距离,最简单的计算方法就是将每段时间内行驶过的距离相累加起来。
<ignore_js_op>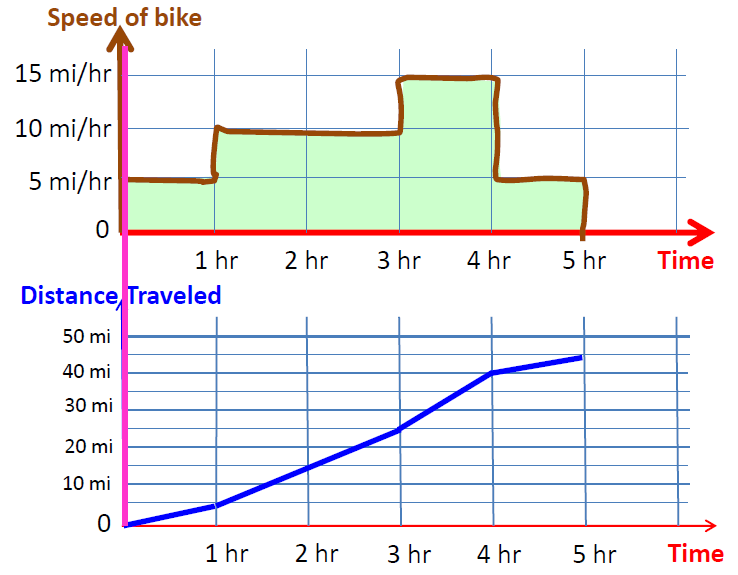

我们通过将每段时间内的速度与时间相乘来计算总距离:
<ignore_js_op>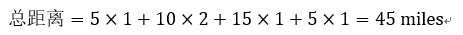
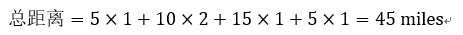
所以5小时内自行车行驶过的总距离是45miles。
现在我们将上述累加距离的过程在一张新的坐标图中用一个一个点标出,并用直线将这些点两两相连,这样就可以得到第二幅图,这幅图展现的就是自行车行驶距离叠加的过程。可以看到,第二幅图尾端所对应的数值为45miles。
实际上,上面的将每一小段时间内行驶过的距离累加起来的过程就是积分的一个过程。其实我们可以换一种角度来看,求积分的过程也可以理解为求函数下方面积的过程,在这个例子中,上图中被涂成绿色的面积就等于自行车行驶过的总过程。从上述自行车的例子中可以看出,积分的过程实际上就是找出函数下方面积的过程,举个例子,假设我们现在要对下图中的函数f(x)进行积分,那么积分后的表达式应该被写为:
<ignore_js_op>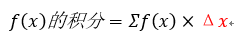
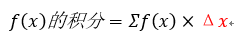
我们可以通过下面两幅图来理解一下这个积分的表达式:从下图中可以看到,对于每一个小长方形我们用长乘宽的方式将它们各自的面积求出,这些小长方形的宽,长为每一个横坐标在函数f(x)上对应的值。从左图中可以看到,如果我们将这些小长方形的面积叠加就可以粗略得估算出函数下的面积,如果我们设置得非常小(如右图),那我们就可以较为精准地求出函数下的面积,也就是函数的积分值。
<ignore_js_op>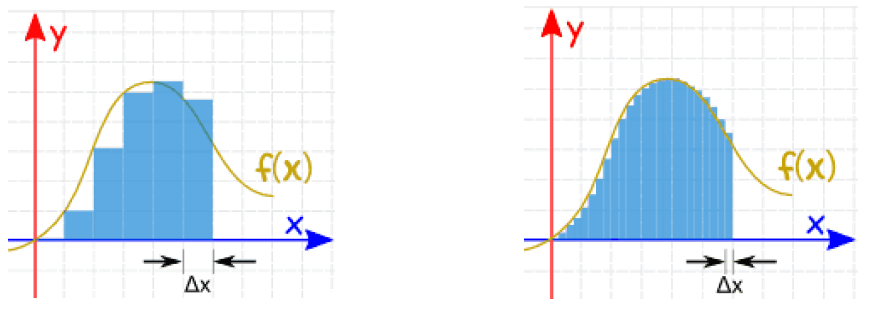

再让我们回顾一下Jack 和Jill的例子,这里大家可以回想一下之前的Hill()函数的导函数HillSlope()么,如果我们现在想求它的积分函数,我们只要将HillSlope()下的面积叠加起来便可以得到最原始的Hill()函数。这也验证了我们之前说的积分是微分的逆运算这一说法。
<ignore_js_op>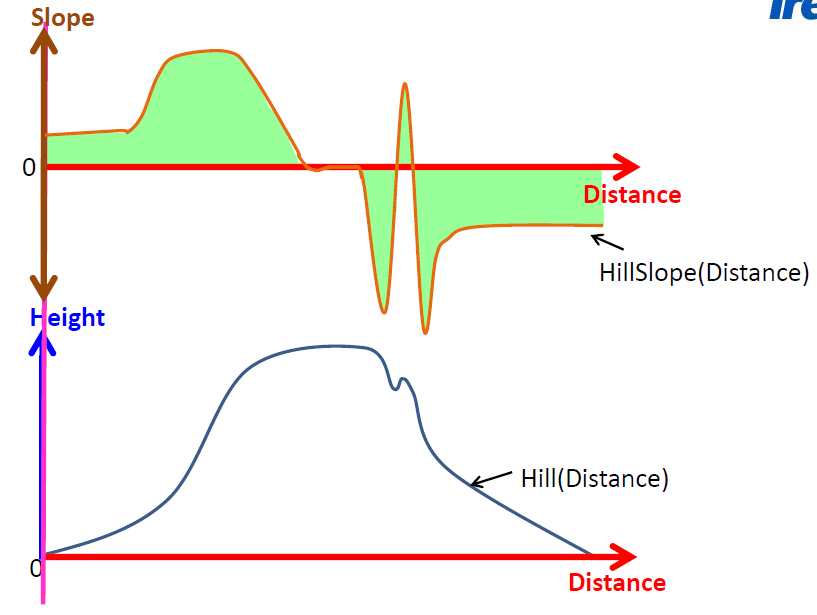

以上是关于转RM论坛 控制技术 PID控制中的I与D的主要内容,如果未能解决你的问题,请参考以下文章