leetcode二分 | 牛顿迭代法69_Sqrt(x)
Posted osea
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了leetcode二分 | 牛顿迭代法69_Sqrt(x)相关的知识,希望对你有一定的参考价值。
题目链接:传送门
题目描述:
求Sqrt(x),返回整数值即可。
【代码】:

1 #include<bits/stdc++.h> 2 using namespace std; 3 const int N = 1e6+10 ; 4 /* 5 int mySqrt ( int x ) 6 int L = 1 , R = N , mid , ans = 0 ; 7 while ( L <= R ) 8 mid = ( L + R ) >> 1 ; 9 if( mid <= x / mid ) 10 L = mid + 1 ; 11 ans = mid ; 12 else 13 R = mid - 1 ; 14 15 16 return ans ; 17 18 */ 19 int mySqrt ( int x ) 20 if ( !x ) 21 return 0 ; 22 double eps = 1e-4; 23 double res = x , Last; 24 while ( true ) 25 Last = res ; 26 res = 0.5 * ( res + x/res ) ; 27 if( fabs( Last - res ) < eps) 28 break ; 29 30 31 return (int)res; 32 33 int main() 34 35 int n; 36 while ( ~scanf("%d",&n) ) 37 printf(" Sqrt (%d) = %d \\n",n,mySqrt(n) ); 38 39 return 0; 40
【题解】:
首先有两个做法。
第一个就是二分法,大家要记住,这个方法需要判溢出,不然会一直错。需要“移乘变除”
第二种方法就是我想写博客来记录的,我觉得真的非常好的一个想法,就是“牛顿迭代法”。
主要参考博客和网站:1、求牛顿开方法的算法及其原理,此算法能开任意次方吗?
以下就是知乎一些比较出色的解答
“黄徐升”的回答:
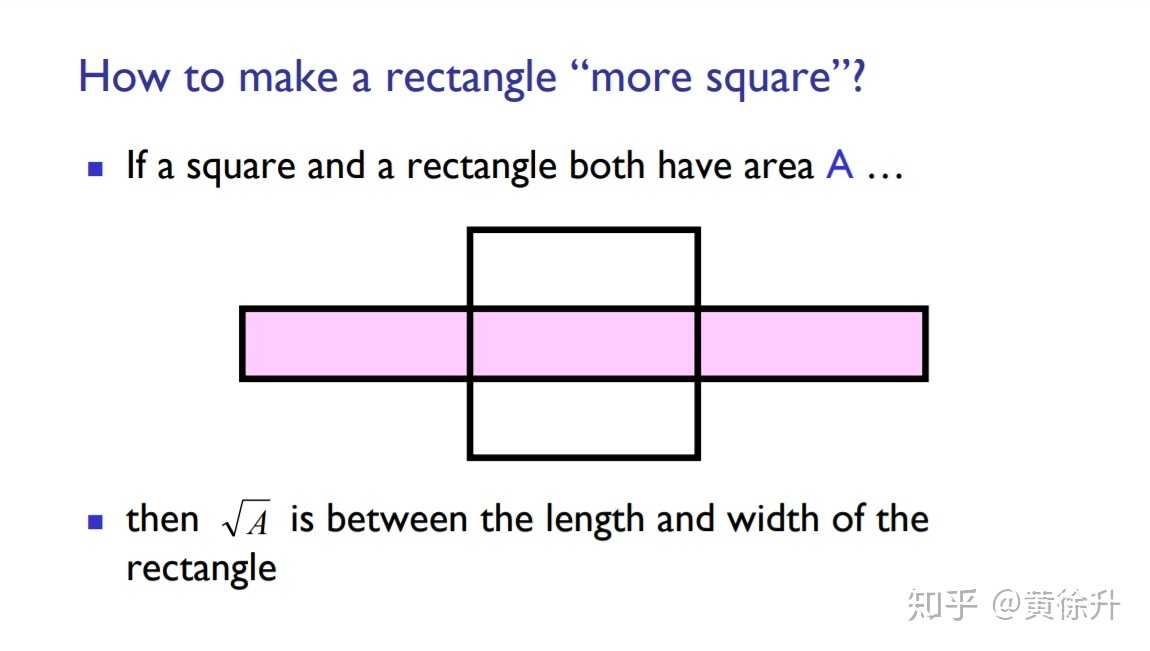
有一个利用“将长方形变得更像正方形”的思路也可以得到求 的算数平方根的迭代公式
算是通俗易懂地得到了这个迭代公式(不过并没有体现牛顿法的求导等过程,那个用抛物线的切线看是比较直观的,别的回答里已经有了)。
首先是考虑 是面积为
的正方形的边长,如果画一个邻边不等的面积是
长方形,设这个长方形的长为
,宽为
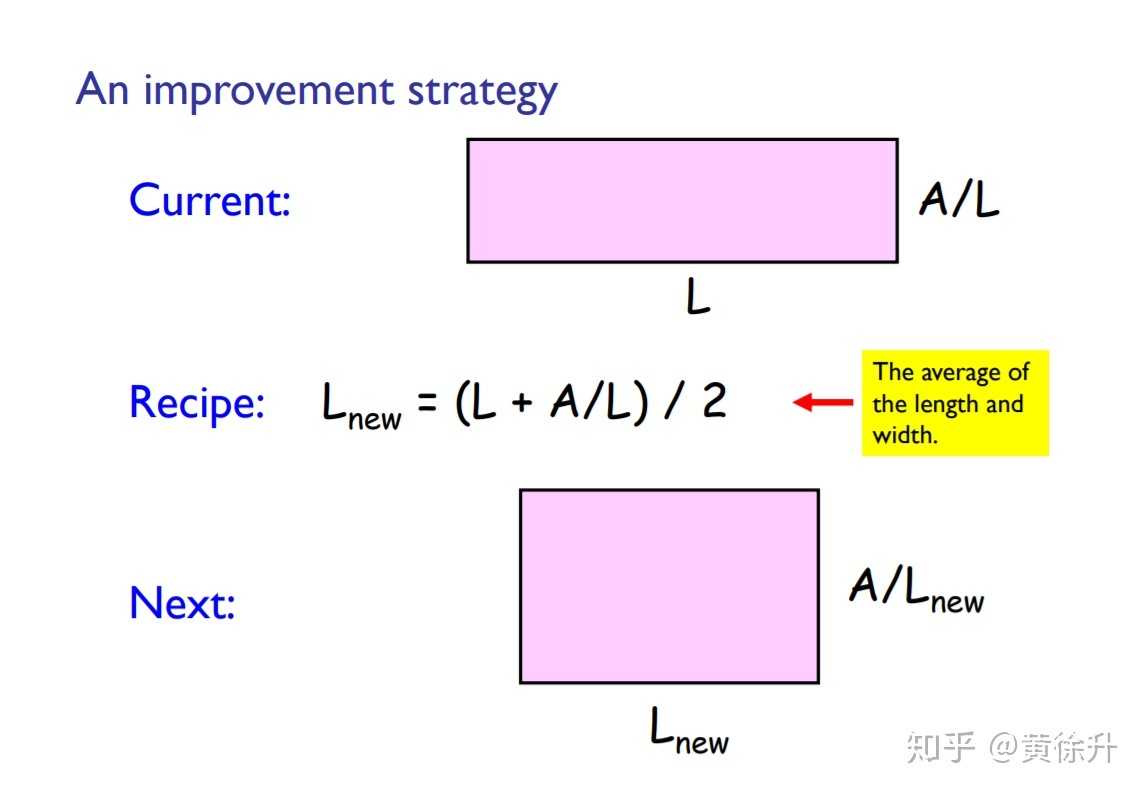
,那么怎样能让这个长方形变得更像一个正方形呢?是要把长变得短一点,宽变得长一点,可以用长和宽的平均数
来作为新的长
,在面积不变的条件下,新的宽是
。这样不断操作下去,长方形的长和宽会越来越接近,就是一直趋近与
了。
【牛顿迭代法】
假设方程 在
附近有一个根,那么用以下迭代式子:
依次计算、
、
、……,那么序列将无限逼近方程的根。
牛顿迭代法的原理很简单,其实是根据f(x)在x0附近的值和斜率,估计f(x)和x轴的交点,看下面的动态图:
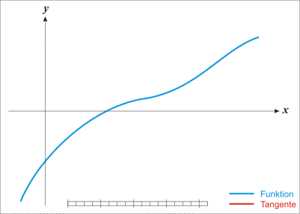
【用牛顿迭代法开平方】
令:
所以f(x)的一次导是:
牛顿迭代式:
随便一个迭代的初始值,例如,代入上面的式子迭代。
例如计算,即a=2。
……
计算器上可给出
【用牛顿迭代法开任意次方】
求的递推式是:
以上是关于leetcode二分 | 牛顿迭代法69_Sqrt(x)的主要内容,如果未能解决你的问题,请参考以下文章
