,k 近邻法
Posted cuancuancuanhao
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了,k 近邻法相关的知识,希望对你有一定的参考价值。
? k 近邻法来分类,用到了 kd 树的建立和搜索
● 代码
1 import numpy as np 2 import matplotlib.pyplot as plt 3 from mpl_toolkits.mplot3d import Axes3D 4 from mpl_toolkits.mplot3d.art3d import Poly3DCollection 5 from matplotlib.patches import Rectangle 6 import operator 7 import warnings 8 9 warnings.filterwarnings("ignore") 10 dataSize = 10000 11 trainRatio = 0.3 12 13 def dataSplit(x, y, part): # 将数据集按给定索引分为两段 14 return x[:part], y[:part],x[part:],y[part:] 15 16 def myColor(x): # 颜色函数,用于对散点染色 17 r = np.select([x < 1/2, x < 3/4, x <= 1, True],[0, 4 * x - 2, 1, 0]) 18 g = np.select([x < 1/4, x < 3/4, x <= 1, True],[4 * x, 1, 4 - 4 * x, 0]) 19 b = np.select([x < 1/4, x < 1/2, x <= 1, True],[1, 2 - 4 * x, 0, 0]) 20 return [r**2,g**2,b**2] 21 22 def mold(x, y): # 距离采用欧氏距离的平方 23 return np.sum((x - y)**2) 24 25 def createData(dim, kind, count = dataSize): # 创建数据集 26 np.random.seed(103) 27 X = np.random.rand(count, dim) 28 center = np.random.rand(kind, dim) 29 Y = [ chr(65 + np.argmin(np.sum((X[i] - center)**2, 1))) for i in range(count) ] 30 #print(output) 31 classCount = dict([ [chr(65 + i),0] for i in range(kind) ]) 32 for i in range(count): 33 classCount[Y[i]] +=1 34 print("dim = %d, kind = %d, dataSize = %d,"%(dim, kind, count)) 35 for i in range(kind): 36 print("kind %c -> %4d"%(chr(65+i), classCount[chr(65+i)])) 37 return X, np.array(Y) 38 39 def buildKdTree(dataX, dataY, dividDim): # 建立 kd 树,每个节点具有的成员有: 40 count, dim = np.shape(dataX) # count 总结点数,dividDim 根节点用来划分空间的坐标的序号 41 if count == 0: # point 根节点坐标,kind 根节点类别 42 return ‘count‘: 0 # leftChild rightChild 左右子节点 43 if count == 1: 44 return ‘count‘: 1, ‘point‘: dataX[0], ‘kind‘: dataY[0] # 总结点只有 0 或者 1 时只有部分成员就够了 45 46 #print(count) # 调试用,显示当前节点情况 47 index = np.lexsort((np.ones(count),dataX[:,dividDim])) # 用 dataX 的值大小来给 dataX 和 dataY 排序,以便查找中位数、切割数据 48 childDataX = dataX[index] 49 childDataY = dataY[index] 50 return ‘count‘: count, ‘index‘: dividDim, ‘point‘: childDataX[count>>1], ‘kind‘: dataY[count>>1], 51 ‘leftChild‘: buildKdTree(childDataX[:count>>1], childDataY[:count>>1], (dividDim + 1) % dim), 52 ‘rightChild‘: buildKdTree(childDataX[(count>>1) + 1:], childDataY[(count>>1) + 1:], (dividDim + 1) % dim) 53 54 def findNearest(origin, nowTree, dividDim): # 搜索 kd 树,寻找最近邻点 55 if nowTree[‘count‘] == 0: # 空子树,返回一个极大的距离 56 return np.inf, ‘?‘ 57 if nowTree[‘count‘] == 1: # 单点子树,返回距离和类别 58 return mold(origin, nowTree[‘point‘]), nowTree[‘kind‘] 59 60 dim = len(origin) 61 moldCenter = mold(origin, nowTree[‘point‘]) # 母节点距离 62 63 if origin[dividDim] < nowTree[‘point‘][dividDim]: # 左支 64 temp = findNearest(origin, nowTree[‘leftChild‘], (dividDim+1)%dim) 65 if origin[dividDim] + temp[0] > nowTree[‘point‘][dividDim]: # 穿透分界线,要算右边,最近点为母节点或新子节点 66 temp = findNearest(origin, nowTree[‘rightChild‘], (dividDim+1)%dim) # 没穿分界线,不算右边,最近点在母节点或旧子节点 67 else: # 右支 68 temp = findNearest(origin, nowTree[‘rightChild‘], (dividDim+1)%dim) 69 if origin[dividDim] - temp[0] < nowTree[‘point‘][dividDim]: # 穿透分界线,要算左边 70 temp = findNearest(origin, nowTree[‘leftChild‘], (dividDim+1)%dim) # 没穿分界线,不算左边 71 72 if moldCenter < temp[0]: # 所有分支的比较集中在母节点和挑出来的子节点之间 73 return moldCenter, nowTree[‘kind‘] 74 else: 75 return temp 76 77 def vote(point, k, trainX, trainY): # 计算所有距离,选取 78 distance = np.sum((point - trainX)**2, 1) # 计算 79 queue = sorted(list(zip(distance[:k], trainY[:k]))) # 取出前 k 项排好序 80 for j in range(k, len(distance)): 81 if distance[j] < queue[-1][0]: # 每次有更优的点就把 queue 中最差的点替换掉,然后排序 82 queue[-1] = (distance[j], trainY[j]) 83 queue.sort() 84 kindCount = # 投票阶段 85 for line in queue: 86 if line[1] not in kindCount.keys(): 87 kindCount[line[1]] = 0 88 kindCount[line[1]] += 1 89 output = sorted(kindCount.items(),key = operator.itemgetter(1),reverse = True) 90 return output[0][0] 91 92 def test(dim, kind, k): 93 allX, allY = createData(dim, kind) 94 trainX, trainY, testX, testY = dataSplit(allX, allY, int(dataSize * trainRatio)) 95 myResult = np.array([ ‘?‘ for i in range(len(testX)) ]) # 存放测试结果 96 97 if k == 1: # 一个最近邻时使用 kd 树,否则用正常的的计算距离排序 98 tree = buildKdTree(trainX, trainY, 0) 99 for i in range(len(testX)): # 每次循环解决一个测试样本 100 myResult[i] = findNearest(testX[i], tree, 0)[1] 101 else: 102 if k > len(testX): 103 return None 104 for i in range(len(testX)): # 每次循环解决一个测试样本 105 myResult[i] = vote(testX[i], k, trainX, trainY) 106 107 errorRatio = np.sum((myResult != np.array(testY)).astype(int)**2) / (dataSize * (1 - trainRatio)) 108 print("k = %d, errorRatio = %4f\\n"%(k, errorRatio)) 109 if dim >= 4: # 4维以上不画图,只输出测试错误率 110 return 111 112 errorP = [] # 分类错误的点 113 classP = [ [] for i in range(kind) ] # 正确分到各类的的点 114 for i in range(len(testX)): 115 if myResult[i] != testY[i]: 116 errorP.append(testX[i]) 117 else: 118 classP[ord(myResult[i]) - 65].append(testX[i]) 119 errorP = np.array(errorP) 120 classP = [ np.array(classP[i]) for i in range(kind) ] 121 122 fig = plt.figure(figsize=(10, 8)) 123 124 if dim == 1: # 分不同属性维度画图 125 plt.xlim(-0.1, 1.1) 126 plt.ylim(-0.1, 1.1) 127 for i in range(kind): 128 plt.scatter(classP[i][:,0], np.ones(len(classP[i]))*i, color = myColor(i/kind), s = 8, label = "class" + str(i)) 129 if len(errorP) != 0: 130 plt.scatter(errorP[:,0], (errorP[:,0] > 0.5).astype(int), color = myColor(1), s = 16, label = "errorData") 131 R = [ Rectangle((0,0),0,0, color = myColor(i/kind)) for i in range(kind) ] + [ Rectangle((0,0),0,0, color = myColor(1)) ] 132 plt.legend(R, [ "class" + chr(i+65) for i in range(kind) ] + ["errorData"], loc=[0.84, 0.012], ncol=1, numpoints=1, framealpha = 1) 133 134 if dim == 2: 135 plt.xlim(-0.1, 1.1) 136 plt.ylim(-0.1, 1.1) 137 for i in range(kind): 138 plt.scatter(classP[i][:,0], classP[i][:,1], color = myColor(i/kind), s = 8, label = "class" + str(i)) 139 if len(errorP) != 0: 140 plt.scatter(errorP[:,0], errorP[:,1], color = myColor(1), s = 16, label = "errorData") 141 R = [ Rectangle((0,0),0,0, color = myColor(i/kind)) for i in range(kind) ] + [ Rectangle((0,0),0,0, color = myColor(1)) ] 142 plt.legend(R, [ "class" + chr(i+65) for i in range(kind) ] + ["errorData"], loc=[0.84, 0.012], ncol=1, numpoints=1, framealpha = 1) 143 144 if dim == 3: 145 ax = Axes3D(fig) 146 ax.set_xlim3d(-0.1, 1.1) 147 ax.set_ylim3d(-0.1, 1.1) 148 ax.set_zlim3d(-0.1, 1.1) 149 ax.set_xlabel(‘X‘, fontdict=‘size‘: 15, ‘color‘: ‘k‘) 150 ax.set_ylabel(‘Y‘, fontdict=‘size‘: 15, ‘color‘: ‘k‘) 151 ax.set_zlabel(‘Z‘, fontdict=‘size‘: 15, ‘color‘: ‘k‘) 152 for i in range(kind): 153 ax.scatter(classP[i][:,0], classP[i][:,1],classP[i][:,2], color = myColor(i/kind), s = 8, label = "class" + str(i)) 154 if len(errorP) != 0: 155 ax.scatter(errorP[:,0], errorP[:,1],errorP[:,2], color = myColor(1), s = 16, label = "errorData") 156 R = [ Rectangle((0,0),0,0, color = myColor(i/kind)) for i in range(kind) ] + [ Rectangle((0,0),0,0, color = myColor(1)) ] 157 plt.legend(R, [ "class" + chr(i+65) for i in range(kind) ] + ["errorData"], loc=[0.85, 0.02], ncol=1, numpoints=1, framealpha = 1) 158 159 fig.savefig("R:\\\\dim" + str(dim) + "kind" + str(kind) + ".png") 160 plt.close() 161 162 if __name__ == ‘__main__‘: 163 test(2, 2, 1) 164 test(2, 3, 1) 165 test(3, 3, 1) 166 test(4, 3, 1) 167 test(2, 3, 2) 168 test(2, 4, 3) 169 test(3, 3, 2) 170 test(3, 4, 3) 171 test(4, 3, 2) 172 test(4, 4, 4)
● 输出结果
dim = 2, kind = 2, dataSize = 10000, kind A -> 5301 kind B -> 4699 k = 1, errorRatio = 0.011143 dim = 2, kind = 3, dataSize = 10000, kind A -> 2740 kind B -> 3197 kind C -> 4063 k = 1, errorRatio = 0.024714 dim = 3, kind = 3, dataSize = 10000, kind A -> 3693 kind B -> 4232 kind C -> 2075 k = 1, errorRatio = 0.052571 dim = 4, kind = 3, dataSize = 10000, kind A -> 2640 kind B -> 1765 kind C -> 5595 k = 1, errorRatio = 0.121000 dim = 2, kind = 3, dataSize = 10000, kind A -> 2740 kind B -> 3197 kind C -> 4063 k = 2, errorRatio = 0.009857 dim = 2, kind = 4, dataSize = 10000, kind A -> 2740 kind B -> 3000 kind C -> 2387 kind D -> 1873 k = 3, errorRatio = 0.013571 dim = 3, kind = 3, dataSize = 10000, kind A -> 3693 kind B -> 4232 kind C -> 2075 k = 2, errorRatio = 0.028571 dim = 3, kind = 4, dataSize = 10000, kind A -> 3029 kind B -> 3379 kind C -> 917 kind D -> 2675 k = 3, errorRatio = 0.038000 dim = 4, kind = 3, dataSize = 10000, kind A -> 2640 kind B -> 1765 kind C -> 5595 k = 2, errorRatio = 0.062286 dim = 4, kind = 4, dataSize = 10000, kind A -> 2472 kind B -> 1752 kind C -> 3365 kind D -> 2411 k = 4, errorRatio = 0.079429
● 画图
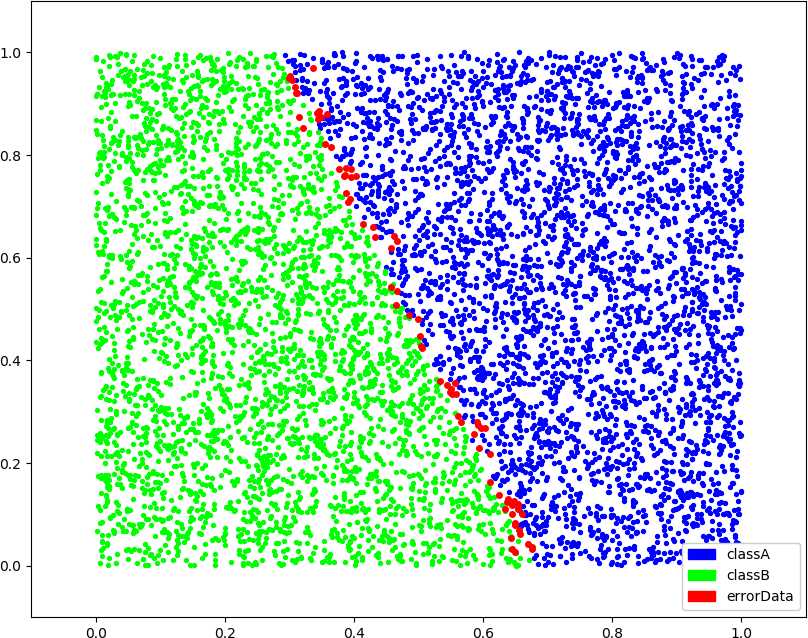
以上是关于,k 近邻法的主要内容,如果未能解决你的问题,请参考以下文章