后缀数组入门

Posted 2022-03-21 --zz

博主睡觉了，明天继续

后缀数组的定义:

后缀数组 (Suffix Array) 指某个字符串的所有后缀按字典排序后得到的数组。数组中只保存后缀开始的位置。

后缀：从某个字符串的某个开始位置到其末尾的字符串子串,包括原串和空字符串。

例子：ABC的后缀ABC,BC,C,

字典排序: 默认从小到大

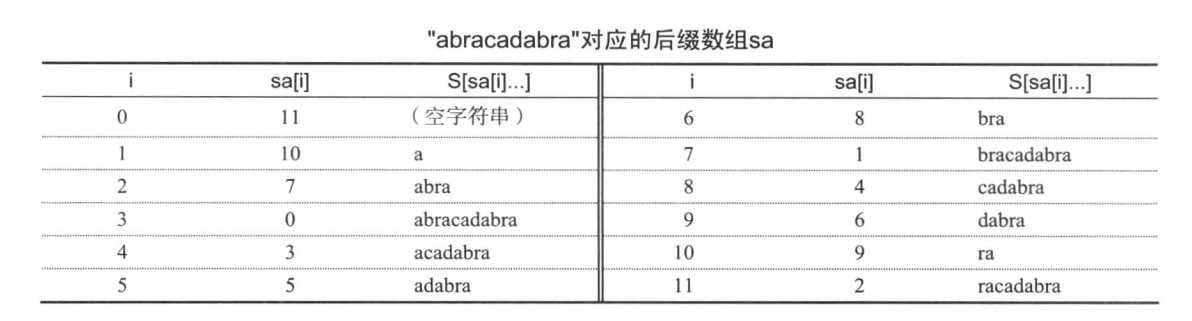
构造后缀数组:

• 朴素做法：将n个字符串进行sort排序,时间复杂度\\(O(n^2log_2n)\\)

• 倍增数组法: Manber和Myers发明,需要进行 \\(log_2n\\) 次排序,排序时间复杂度 \\(O(nlog_2n)\\) ,所以总时间复杂度是 \\(O(nlog_2^2n)\\) ,可以用基数排序将sort排序进行优化,总时间复杂度优化成 \\(O(nlog_2n)\\)。

• 所以一般来说,倍增数组的方法够用了,更快的可以去找[SA-IS 算法]

倍增数组的代码:

未优化代码

#include <cstdio>
#include <cstring>
#include <algorithm>
#define MAXN 1000
using namespace std;

char str[MAXN];//字符串数组
int sa[MAXN + 1];//后缀数组,+1是为了存储(空字符串)
int rank[MAXN + 1];//Rank[i]第i位开始的子串排名(0~N)
int tmp[MAXN+1];
int k,n;

bool cmp_sa(const int &i,const int &j) 
    if(rank[i] != rank[j])  return rank[i]<rank[j];
    else 
        int l = n-i>=k?rank[i+k]:-1;
        int r = n-j>=k?rank[j+k]:-1;
        return l<r;
    
    return true;


void build_sa(const char* str,int *sa) 
    n = strlen(str);
    //长度为1的sa,rank取编码,因为空字符串排最前,所以取-1
    for(int i=0; i<=n; i++) 
        sa[i] = i;
        rank[i] = rank[i] < n? str[i]:-1;
    
    //用长度为i的Rank求长度为k的Rank
    for(k=1; k<=n; k*=2) 
        sort(sa,sa+n+1,cmp_sa);
        tmp[sa[0]] = 0;
        for(int i=1; i<=n; i++) //计算Rank
            tmp[sa[i]] = tmp[sa[i-1]] + (cmp_sa(sa[i-1],sa[i])?1:0);
        
        for(int i=0; i<=n; i++) 
            rank[i] = tmp[i];
        
    


int main() 
    scanf("%s",&str);
    build_sa(str,sa);
    return 0;

题目:

• Best Cow Line(数据加强版)

• 未完待续

参考博客和文献:

https://www.cnblogs.com/jinkun113/p/4743694.html
https://www.cnblogs.com/victorique/p/8480093.html
挑战程序设计竞赛（第2版）