P3327 [SDOI2015]约数个数和

Posted 2022-03-20 lltyyc

传送门

首先证明 $d(ij)=\\sum_k|i\\sum_l|j[gcd(k,l)==1]$

把 $i,j$ 考虑成唯一分解后的形式：$P_i1^k1P_i2^k2...P_in^kn$

对于 $i,j$ 中某个相同的质因子 $P_x$ ，$i=...P_x^ki...$，$j=...P_x^kj...$

如果枚举到 $j$ 中因数 $l$ 时，$l$ 有因数 $P_x^t$，不妨看成 $P_x^ki+t$，

如果这样看，那么会发现枚举 $k,l$ 时一定能把 $P_x$ 从 $P_x^1$ 枚举到 $P_x^ki+kj$，这样就包括了所有情况

会不会重复算呢，显然因为式子 $d(ij)=\\sum_k|i\\sum_l|j[gcd(k,l)==1]$ 要满足 $k,l$ 没有相同的质因数才有贡献

所以枚举时对于同一个质因数一定不会在既在 $k$ 中有，又在 $l$ 中有，

即不会出现枚举成 $P_x^ki+t+y$，其中 $y$ 是 $k$ 对 $P$ 的贡献（此时 $k$ 的贡献已经全在 $ki$ 中了，导致不合法）

要么是 $P_x^ki+t$ 要么是 $P_x^y$

所以最后我们证明了 $d(ij)=\\sum_k|i\\sum_l|j[gcd(k,l)==1]$

那么 $Ans=\\sum_i\\sum_jd(ij)=\\sum_k|i\\sum_l|j[gcd(k,l)==1]$

有 $gcd$ 了，显然莫比乌斯反演：

设 $f[x]=\\sum_i\\sum_j\\sum_k|i\\sum_l|j[gcd(k,l)==x]$，答案即为 $f[1]$

设 $F[x]=\\sum_i\\sum_j\\sum_k|i\\sum_l|j[x|gcd(k,l)]$，那么有 $F[x]=\\sum_x|df[d]$，直接反演得到

$f[1]=\\sum_d\\mu(d)\\sum_i\\sum_j\\sum_k|i\\sum_l|j[d|gcd(k,l)]$

变成先枚举 $k,l$ 再枚举 $k,l$ 的倍数 $i‘,j‘$，使得 $ki‘=i,kj‘=j$，变成

$f[1]=\\sum_d\\mu(d)\\sum_k\\sum_l[d|gcd(k,l)]\\sum_i‘^\\left \\lfloor \\fracNk \\right \\rfloor\\sum_j‘^\\left \\lfloor \\fracMl \\right \\rfloor\\\\=\\sum_d\\mu(d)\\sum_k^N\\sum_l^M[d|gcd(k,l)]\\left \\lfloor \\fracNk \\right \\rfloor\\left \\lfloor \\fracMl \\right \\rfloor$

把枚举数 $k,l$ 变成枚举 $d$ 的倍数 $k‘,l‘$，使得 $k=k‘d,l=l‘d$，得到

$f[1]=\\sum_d\\mu(d)\\sum_k‘^\\left \\lfloor \\fracNd \\right \\rfloor\\sum_l‘^\\left \\lfloor \\fracMd \\right \\rfloor\\left \\lfloor \\fracNk‘d \\right \\rfloor\\left \\lfloor \\fracMl‘d \\right \\rfloor\\\\=\\sum_d\\mu(d)(\\sum_k‘^\\left \\lfloor \\fracNd \\right \\rfloor\\left \\lfloor \\fracNk‘d \\right \\rfloor)(\\sum_l‘^\\left \\lfloor \\fracMd \\right \\rfloor\\left \\lfloor \\fracMl‘d \\right \\rfloor)\\\\=\\sum_d\\mu(d)(\\sum_k‘^\\left \\lfloor \\fracNd \\right \\rfloor\\left \\lfloor \\frac\\left \\lfloor \\fracNd \\right \\rfloork‘ \\right \\rfloor)(\\sum_l‘^\\left \\lfloor \\fracMd \\right \\rfloor\\left \\lfloor \\frac\\left \\lfloor \\fracMd \\right \\rfloorl‘ \\right \\rfloor)$

只要预处理出 $sum[x]=\\sum_k‘^\\left \\lfloor \\fracNd \\right \\rfloor\\left \\lfloor \\frac\\left \\lfloor \\fracNd \\right \\rfloork‘ \\right \\rfloor$ 就好了

 最后附上完整过程：

 

 

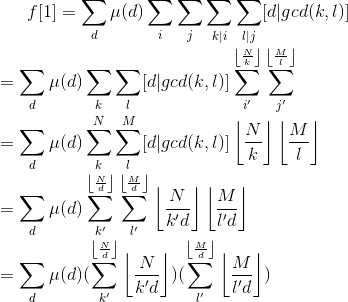
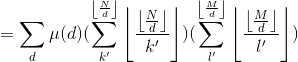
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
typedef long long ll;
inline int read()

    int x=0,f=1; char ch=getchar();
    while(ch<‘0‘||ch>‘9‘)  if(ch==‘-‘) f=-1; ch=getchar(); 
    while(ch>=‘0‘&&ch<=‘9‘)  x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); 
    return x*f;

const int N=2e7+7;
int Q,n,m,mi,pri[N],mu[N],tot;
ll sum[N],ans;
bool not_pri[N];
void pre()

    not_pri[1]=1; mu[1]=1;
    for(int i=2;i<5e4;i++)
    
        if(!not_pri[i]) pri[++tot]=i,mu[i]=-1;
        for(int j=1;j<=tot;j++)
        
            ll t=1ll*i*pri[j]; if(t>5e4) break;
            not_pri[t]=1; if(!(i%pri[j])) break;
            mu[t]=-mu[i];
        
    
    for(int i=2;i<=5e4;i++) mu[i]+=mu[i-1];

int main()

    Q=read(); pre();
       for(int i=1;i<=5e4;i++)
    
           for(int l=1,r;l<=i;l=r+1)
           
               r=i/(i/l);
               sum[i]+=1ll*(r-l+1)*(i/l);
           
    
    while(Q--)
    
        n=read(),m=read(); mi=min(n,m); ans=0;
        for(int l=1,r;l<=mi;l=r+1)
        
            r=min(n/(n/l),m/(m/l));
            ans+=1ll*(mu[r]-mu[l-1])*sum[n/l]*sum[m/l];
        
        printf("%lld\\n",ans);
    
    return 0;