（数据科学学习手札62）详解seaborn中的kdeplotrugplotdistplot与jointplot

Posted 2022-03-13 feffery

一、简介

　　seaborn是Python中基于matplotlib的具有更多可视化功能和更优美绘图风格的绘图模块，当我们想要探索单个或一对数据分布上的特征时，可以使用到seaborn中内置的若干函数对数据的分布进行多种多样的可视化，本文以jupyter notebook为编辑工具，针对seaborn中的kdeplot、rugplot、distplot和jointplot，对其参数设置和具体用法进行详细介绍。 

 

二、kdeplot

　　seaborn中的kdeplot可用于对单变量和双变量进行核密度估计并可视化，其主要参数如下：

　　data：一维数组，单变量时作为唯一的变量

　　data2：格式同data2，单变量时不输入，双变量作为第2个输入变量

　　shade：bool型变量，用于控制是否对核密度估计曲线下的面积进行色彩填充，True代表填充

　　vertical：bool型变量，在单变量输入时有效，用于控制是否颠倒x-y轴位置

　　kernel：字符型输入，用于控制核密度估计的方法，默认为‘gau‘，即高斯核，特别地在2维变量的情况下仅支持高斯核方法

　　legend：bool型变量，用于控制是否在图像上添加图例

　　cumulative：bool型变量，用于控制是否绘制核密度估计的累计分布，默认为False

　　shade_lowest：bool型变量，用于控制是否为核密度估计中最低的范围着色，主要用于在同一个坐标轴中比较多个不同分布总体，默认为True

　　cbar：bool型变量，用于控制是否在绘制二维核密度估计图时在图像右侧边添加比色卡

　　color：字符型变量，用于控制核密度曲线色彩，同plt.plot()中的color参数，如‘r‘代表红色

　　cmap：字符型变量，用于控制核密度区域的递进色彩方案，同plt.plot()中的cmap参数，如‘Blues‘代表蓝色系

　　n_levels：int型，在而为变量时有效，用于控制核密度估计的区间个数，反映在图像上的闭环层数

　　下面我们来看几个示例来熟悉kdeplot中上述参数的实际使用方法：

　　首先我们需要准备数据，本文使用seaborn中自带的鸢尾花数据作为示例数据，因为在jupyter notebook中运行代码，所以加上魔术命令%matplotlib inline使得图像得以在notebook中显示

import seaborn as sns
sns.set(color_codes=True)
import matplotlib.pyplot as plt
%matplotlib inline
#加载seaborn自带的鸢尾花数据集，格式为数据框
iris = sns.load_dataset(‘iris‘)
#分离出setosa类的花对应的属性值
setosa = iris.loc[iris.species == "setosa"].reset_index(drop=True)
#分离出virginica类的花对应的属性值
virginica = iris.loc[iris.species == "virginica"].reset_index(drop=True)

　　首先我们不修改其他参数只传入数据来观察绘制出的图像：

#绘制iris中petal_width参数的核密度估计图
ax = sns.kdeplot(iris.petal_width)

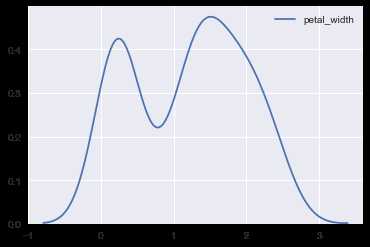
　　加上红色填充颜色，并禁止图例显示：

ax = sns.kdeplot(iris.petal_width,shade=True,color=‘r‘)

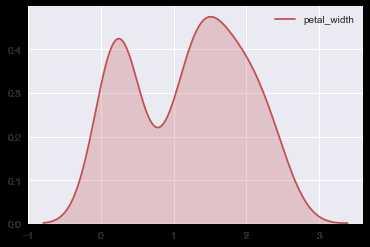
　　修改为核密度分布：

ax = sns.kdeplot(iris.petal_width,
                 shade=True,
                 color=‘r‘,
                 cumulative=True)

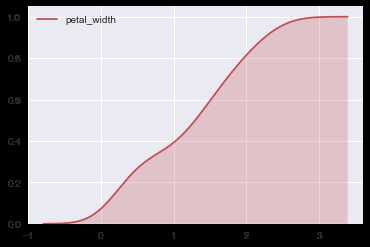
　　交换x-y轴位置：

ax = sns.kdeplot(iris.petal_width,
                 shade=True,
                 color=‘r‘,
                 vertical=True)

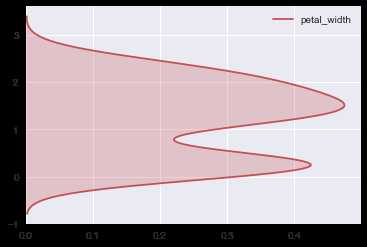
　　下面我们来绘制双变量联合核密度估计图：

#绘制setosa花的petal_width与petal_length的联合核密度估计图
ax = sns.kdeplot(setosa.petal_width,
                 setosa.petal_length)

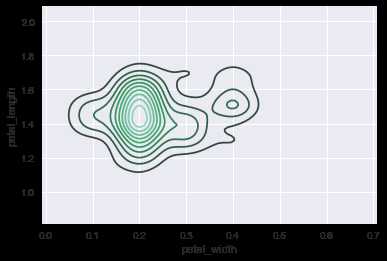
　　修改调色方案为蓝色，并设置shade_lowest=True：

ax = sns.kdeplot(setosa.petal_width,
                 setosa.petal_length,
                 cmap=‘Blues‘,
                 shade=True,
                 shade_lowest=True)

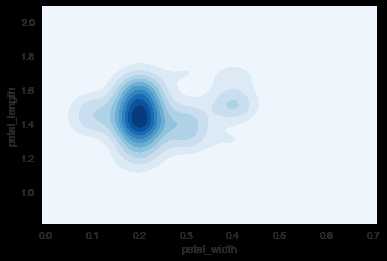
　　在上图基础上修改shade_lowest=False：

ax = sns.kdeplot(setosa.petal_width,
                 setosa.petal_length,
                 cmap=‘Blues‘,
                 shade=True,
                 shade_lowest=False)

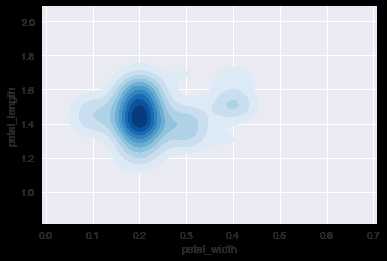
可以看到这时最低密度估计曲线之外的区域没有被调色方案所浸染。

　　将核密度曲线区间个数修改为5：

ax = sns.kdeplot(setosa.petal_width,
                 setosa.petal_length,
                 cmap=‘Blues‘,
                 shade=True,
                 shade_lowest=False,
                 n_levels=5)

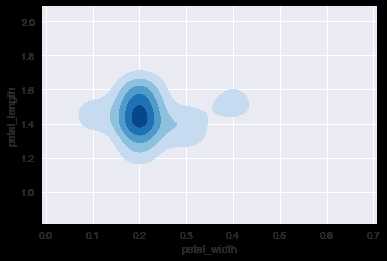
可以看到这时的核密度区间要粗略很多。

　　在同一个子图中绘制两个不同一维总体的核密度估计图，这里为了把它们区分开分别定义了label参数以显示在图例中：

ax1 = sns.kdeplot(setosa.petal_width,label=‘setosa.petal_width‘)
ax2 = sns.kdeplot(virginica.petal_width,label=‘virginica.petal_width‘)

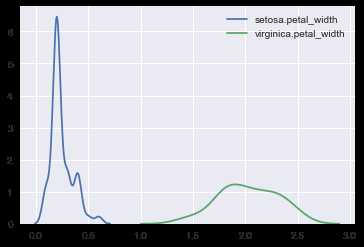
　　在同一个子图中绘制两个不同二维总体的核密度估计图：

ax1 = sns.kdeplot(setosa.sepal_width,setosa.sepal_length,
                  cmap=‘Blues‘,
                  shade=True,
                  shade_lowest=False)
ax2 = sns.kdeplot(virginica.sepal_width,virginica.sepal_length,
                  cmap=‘Greens‘,
                  shade=True,
                  shade_lowest=False)

 

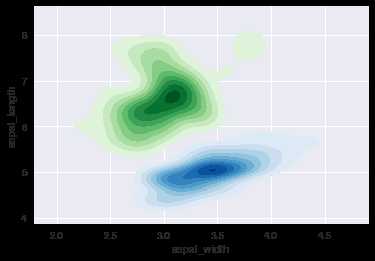
三、rugplot

　　rugplot的功能非常朴素，用于绘制出一维数组中数据点实际的分布位置情况，即不添加任何数学意义上的拟合，单纯的将记录值在坐标轴上表现出来，相对于kdeplot，其可以展示原始的数据离散分布情况，其主要参数如下：

　　a：一维数组，传入观测值向量

　　height：设置每个观测点对应的小短条的高度，默认为0.05

　　axis：字符型变量，观测值对应小短条所在的轴，默认为‘x‘，即x轴

　　

　　使用默认参数进行绘制：

ax = sns.rugplot(iris.petal_length)

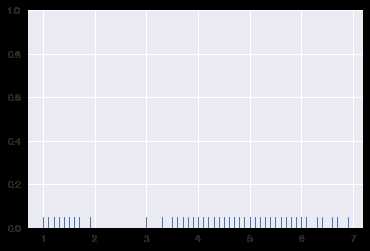
　　调换所处的坐标轴：

ax = sns.rugplot(iris.petal_length,axis=‘y‘)

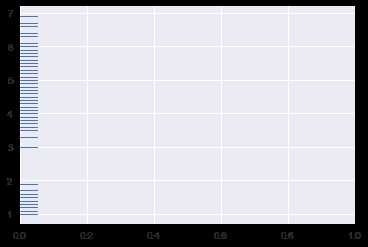
　　修改小短条高度和颜色：

ax = sns.rugplot(iris.petal_length,
                 color=‘r‘,
                 height=0.2)

 

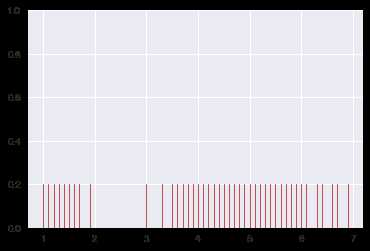
三、distplot

　　seaborn中的distplot主要功能是绘制单变量的直方图，且还可以在直方图的基础上施加kdeplot和rugplot的部分内容，是一个功能非常强大且实用的函数，其主要参数如下：

　　a：一维数组形式，传入待分析的单个变量

　　bins：int型变量，用于确定直方图中显示直方的数量，默认为None，这时bins的具体个数由Freedman-Diaconis准则来确定

　　hist：bool型变量，控制是否绘制直方图，默认为True

　　kde：bool型变量，控制是否绘制核密度估计曲线，默认为True

　　rug：bool型变量，控制是否绘制对应rugplot的部分，默认为False

　　fit：传入scipy.stats中的分布类型，用于在观察变量上抽取相关统计特征来强行拟合指定的分布，下文的例子中会有具体说明，默认为None，即不进行拟合

　　hist_kws,kde_kws,rug_kws：这几个变量都接受字典形式的输入，键值对分别对应各自原生函数中的参数名称与参数值，在下文中会有示例

　　color：用于控制除了fit部分拟合出的曲线之外的所有对象的色彩

　　vertical：bool型，控制是否颠倒x-y轴，默认为False，即不颠倒

　　norm_hist：bool型变量，用于控制直方图高度代表的意义，为True直方图高度表示对应的密度，为False时代表的是对应的直方区间内记录值个数，默认为False

　　label：控制图像中的图例标签显示内容

　　

　　使用默认参数进行绘制：

ax = sns.distplot(iris.petal_length)

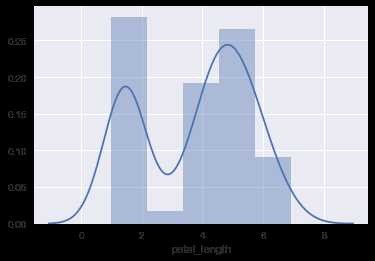
　　修改所有对象的颜色，绘制rugplot部分，并修改bins为20：

ax = sns.distplot(iris.petal_length,color=‘r‘,
                 rug=True,
                 bins=20)

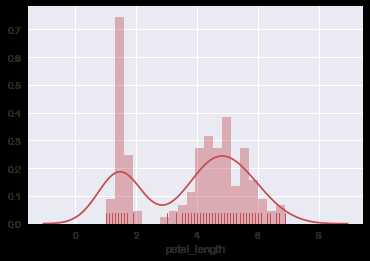
　　在上图的基础上强行拟合卡方分布并利用参数字典设置fit曲线为绿色：

from scipy.stats import chi2                
ax = sns.distplot(iris.petal_length,color=‘r‘,
                 rug=True,
                 bins=20,
                 fit=chi2,
                 fit_kws=‘color‘:‘g‘)

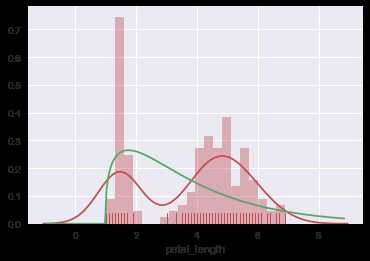
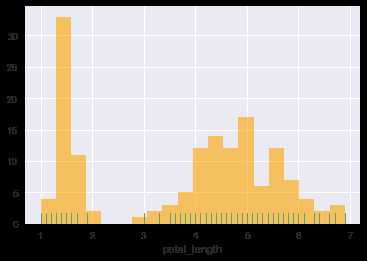
　　修改norm_hist参数为False使得纵轴显示的不再是密度而是频数（注意这里必须关闭kde和fit绘图的部分，否则纵轴依然显示密度），利用hist_kws传入字典调整直方图部分色彩和透明度，利用rug_kws传入字典调整rugplot部分小短条色彩：

ax = sns.distplot(iris.petal_length,color=‘r‘,
                 rug=True,
                 kde=False,
                 bins=20,
                 fit=None,
                 hist_kws=‘alpha‘:0.6,‘color‘:‘orange‘,
                 rug_kws=‘color‘:‘g‘,
                 norm_hist=False)

 

四、jointplot

　　之所以按照kdeplot-rugplot-distplot的顺序来介绍是因为distplot中涉及到kdeplot与rugplot中的相关内容，而本文最后要介绍的函数jointplot中聚合了前面所涉及到的众多内容，用于对成对变量的相关情况、联合分布以及各自的分布在一张图上集中呈现，其主要参数如下：

　　x,y：代表待分析的成对变量，有两种模式，第一种模式：在参数data传入数据框时，x、y均传入字符串，指代数据框中的变量名；第二种模式：在参数data为None时，x、y直接传入两个一维数组，不依赖数据框

　　data：与上一段中的说明相对应，代表数据框，默认为None

　　kind：字符型变量，用于控制展示成对变量相关情况的主图中的样式

　　color：控制图像中对象的色彩

　　height：控制图像为正方形时的边长

　　ratio：int型，调节联合图与边缘图的相对比例，越大则边缘图越矮，默认为5

　　space：int型，用于控制联合图与边缘图的空白大小

　　xlim,ylim：设置x轴与y轴显示范围

　　joint_kws,marginal_kws,annot_kws：传入参数字典来分别精细化控制每个组件

　　

　　在默认参数设置下绘制成对变量联合图：

ax = sns.jointplot(x=‘sepal_length‘,y=‘sepal_width‘,data=setosa)

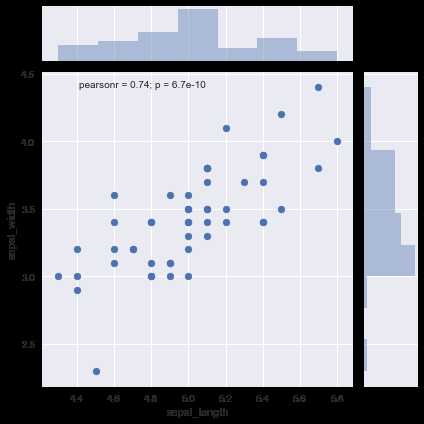
值得一提的是，jointplot还贴心的在图像上说明了成对变量之间的皮尔逊简单相关系数以及相关性检验的p值结果。

　　将kind参数设置为‘reg‘，为联合图添加线性回归拟合直线与核密度估计结果：

ax = sns.jointplot(x=‘sepal_length‘,y=‘sepal_width‘,data=setosa,
                  kind=‘reg‘)

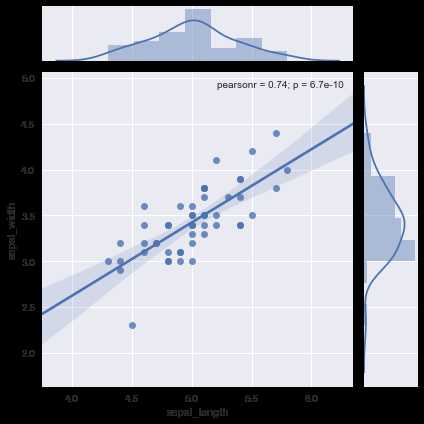
　　修改kind为‘hex‘来为联合图生成六边形核密度估计：

ax = sns.jointplot(x=‘sepal_length‘,y=‘sepal_width‘,data=setosa,
                  kind=‘hex‘)

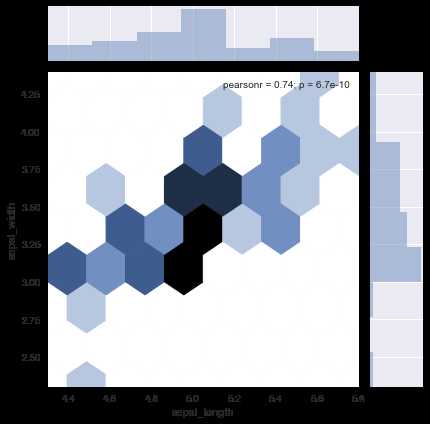
　　修改kind为‘kde‘来将直方图和散点图转换为核密度估计图，并将边际轴的留白大小设定为0：

ax = sns.jointplot(x=‘sepal_length‘,y=‘sepal_width‘,data=setosa,
                   kind=‘kde‘,
                   space=0,
                   color=‘g‘)

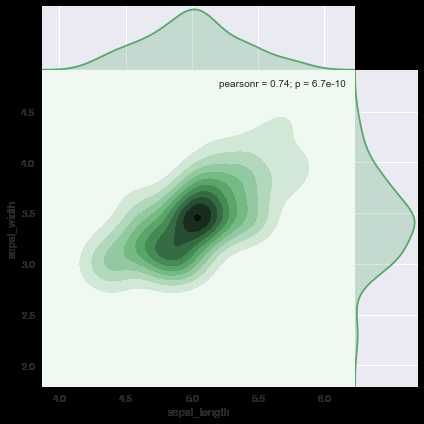
　　jointplot还支持图层叠加，如下面的例子，我们首先绘制出的联合图中kind限制为拟合线性回归直线，在此基础上利用.plot_joint方法叠加核密度估计图层：

ax = (sns.jointplot(x=‘sepal_length‘,y=‘sepal_width‘,data=setosa,
                   color=‘g‘,
                   kind=‘reg‘)).plot_joint(sns.kdeplot, zorder=0, n_levels=10)

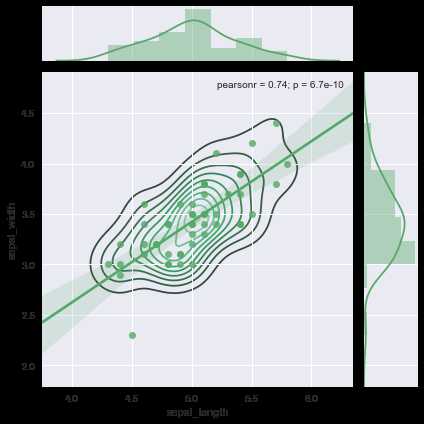
根据你的具体需要还可以叠加出更加丰富的图像。

　　调大ratio参数使得边缘图更加小巧：

ax = sns.jointplot(x=‘sepal_length‘,y=‘sepal_width‘,data=setosa,
                   kind=‘kde‘,
                   space=0,
                   color=‘g‘,
                   ratio=15)

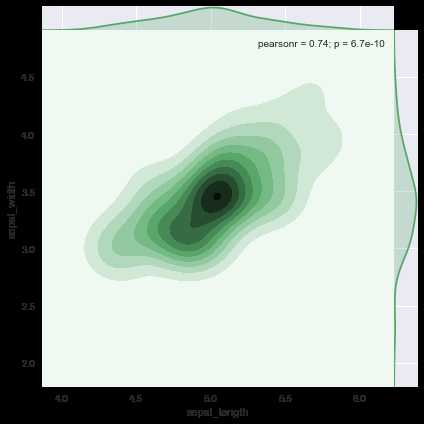
　　利用边缘图形参数字典为边缘图形添加rugplot的内容，并修改直方个数为15：

ax = sns.jointplot(x=‘sepal_length‘,y=‘sepal_width‘,data=setosa,
                   marginal_kws=dict(bins=15, rug=True),
                   linewidth=1,space=0)

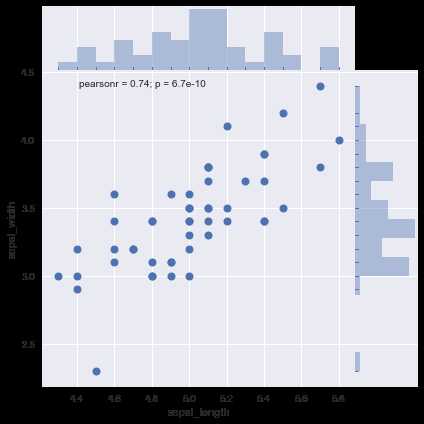
　　实际上，如果你足够了解matplotlib与seaborn，可以通过各种组合得到信息量更丰富特别的图像！

 

 

　　以上就是本文的全部内容，如有笔误望指出！