Levenshtein distance 编辑距离算法

Posted jfdwd

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Levenshtein distance 编辑距离算法相关的知识，希望对你有一定的参考价值。

这几天再看 virtrual-dom，关于两个列表的对比，讲到了 Levenshtein distance 距离，周末抽空做一下总结。

Levenshtein Distance 介绍

在信息理论和计算机科学中，Levenshtein 距离是用于测量两个序列之间的差异量（即编辑距离）的度量。两个字符串之间的 Levenshtein 距离定义为将一个字符串转换为另一个字符串所需的最小编辑数，允许的编辑操作是单个字符的插入，删除或替换。

例子

‘kitten’和’sitten’之间的 Levenshtein 距离是 3，因为一下三个编辑将一个更改为另一个，并且没有办法用少于三个编辑来执行操作。

  1. k itten sitten => 用’s’代替’k’
  2. sitt e n sitt i => 用’i’代替’e’
  3. sittin sittin g 在结尾插入’g’

Levenshtein Distance (编辑距离) 算法详解

为了得到编辑距离，我们用 beauty 和 batyu 为例：

技术图片

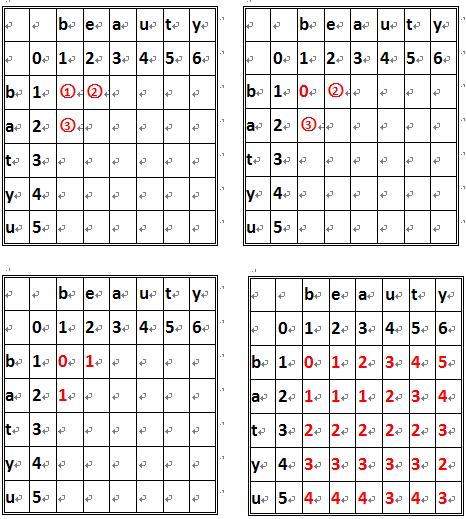
图示如 ① 单元位置是两个单词的第一个字符 [b] 比较得到的值，其的值有它的上方的值 (1)、它左方的值 (1) 和它左上角的值 (0) 来决定。当单元格所在的行和列所对应的字符相等时，单元格的值为左上方的值。

否则，单元格左上角的值与其上方和左方的值进行比较，它们之间的最小值 + 1 即是单元格的值。

图中 ① 的值由于单元格行和列相等，所以取左上角值 0。

图中 ② 的值由于单元格行列不相等，(1, 2, 0) 取最小为 0， 结果 + 1， 所以 ② 值为 1。

图示 ③ 的值由于单元格行列不相等，(1, 0, 2) 取最小 0， 结果 + 1， 所以 ③ 值为 1。

算法证明

这个算法计算的是将 s [1…i] 转换为 t [1…j]（例如将 beauty 转换为 batyu）所需最少的操作数（也就是所谓的编辑距离），这个操作数被保存在 d [i,j]（d 代表的就是上图所示的二维数组）中。

  • 在第一行与第一列肯定是正确的，这也很好理解，例如我们将 beauty 转换为空字符串，我们需要进行的操作数为 beauty 的长度（所进行的操作为将 beauty 所有的字符丢弃）。
  • 我们对字符的可能操作有三种：
  • 将 s [1…n] 转换为 t [1…m] 当然需要将所有的 s 转换为所有的 t，所以，d [n,m]（表格的右下角）就是我们所需的结果。
  • 如果我们可以使用 k 个操作数把 s [1…i] 转换为 t [1…j-1]，我们只需要把 t [j] 加在最后面就能将 s [1…i] 转换为 t [1…j]，操作数为 k+1
  • 如果我们可以使用 k 个操作数把 s [1…i-1] 转换为 t [1…j]，我们只需要把 s [i] 从最后删除就可以完成转换，操作数为 k+1
  • 如果我们可以使用 k 个操作数把 s [1…i-1] 转换为 t [1…j-1]，我们只需要在需要的情况下（s [i] != t [j]）把 s [i] 替换为 t [j]，所需的操作数为 k+cost（cost 代表是否需要转换，如果 s [i]==t [j]，则 cost 为 0，否则为 1）。

可能的改进

  • 现在的算法复杂度为 O (m*n)，可以将其改进为 O (m)。因为这个算法只需要上一行和当前行被存储下来就可以了。
  • 如果需要重现转换步骤，我们可以把每一步的位置和所进行的操作保存下来，进行重现。
  • 如果我们只需要比较转换步骤是否小于一个特定常数 k，那么只计算高宽宽为 2k+1 的矩形就可以了，这样的话，算法复杂度可简化为 O (kl)，l 代表参加对比的最短 string 的长度。
  • 我们可以对三种操作（添加，删除，替换）给予不同的权值（当前算法均假设为 1，我们可以设添加为 1，删除为 0，替换为 2 之类的），来细化我们的对比。
  • 如果我们将第一行的所有 cell 初始化为 0，则此算法可以用作模糊字符查询。我们可以得到最匹配此字符串的字符串的最后一个字符的位置（index number），如果我们需要此字符串的起始位置，我们则需要存储各个操作的步骤，然后通过算法计算出字符串的起始位置。
  • 这个算法不支持并行计算，在处理超大字符串的时候会无法利用到并行计算的好处。但我们也可以并行的计算 cost values（两个相同位置的字符是否相等），然后通过此算法来进行整体计算。
  • 如果只检查对角线而不是检查整行，并且使用延迟验证（lazy evaluation），此算法的时间复杂度可优化为 O (m (1+d))（d 代表结果）。这在两个字符串非常相似的情况下可以使对比速度速度大为增加。

字符串比较代码

这一部分的代码，参考了 https://rosettacode.org/wiki/Levenshtein_distance#ES5

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
 
const ld = (a, b) => 
  let t = [], u, i, j, m = a.length, n = b.length;

  if (!m) return b;
  if (!n) return a;

  for (j = 0; j <= m; j++) 
    t[j] = j;
  

  console.log(t);

  for (i = 1; i <= n; i++) 
    for (u = [i], j = 1; j <= m; j++) 
      u[j] = a[j - 1] === b[i - 1] ? t[j - 1] : Math.min(t[j - 1], t[j], u[j - 1]) + 1  // Levenshtein Distance 算法核心比较部分。
    

    t = u;
    console.log(t);
  

  return u[m];


[[‘beauty‘, ‘batyu‘, 3],
].forEach(function (v) 
  var a = v[0], b = v[1], t = v[2], d = ld(a, b);
  if (d !== t) 
    console.log(‘levenstein("‘ + a + ‘","‘ + b + ‘") was ‘ + d + ‘ should be ‘ + t);
  
);

// 打印出来
[ 0, 1, 2, 3, 4, 5, 6 ]
[ 1, 0, 1, 2, 3, 4, 5 ]
[ 2, 1, 1, 1, 2, 3, 4 ]
[ 3, 2, 2, 2, 2, 2, 3 ]
[ 4, 3, 3, 3, 3, 3, 2 ]
[ 5, 4, 4, 4, 3, 4, 3 ]

还原字符串

上面总结了传统的计算字符串之间的差距，那么当我们怎么能在计算的过程中，记录需要转换的步骤，并且进行还原呢。

这里我们需要对比较的每一位的步骤有一个了解。

为了得到编辑距离，我们用 beauty 和 batyu 为例：
从上面一节的图中可以看到，‘beauty‘ 转换为 ‘‘ ，对一个的第一行的 [1，2，3，4，5，6]，每一个步骤都相对与上一个元素新建一个元素，同理 ‘‘ 转换为 ‘batyu‘，每一个值都是相对一上一个元素的删除步骤。

那么对角线也显而易见就是先相对于替换操作。那么我们现在需要做的就是，记录下相对应的索引和元素以及需要进行的操作，并将其保存为一个对象，每次新增的对象用数组来保存就可以了。

技术图片

1
2
3
4
5
6
7
8
9
10
11
12
13
14
 
const actionType = 
  TYPE_REPLACE: ‘TYPE_REPLACE‘,
  TYPE_NEW: ‘TYPE_NEW‘,
  TYPE_DELETE: ‘TYPE_DELETE‘


// 生成对象的方法
const patchObj = (index, type, item = ‘‘) => 
  return 
    index,
    type,
    item

下面是 compare 方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
 
/**
 * 
 * @param  array  r 替换操作 replace
 * @param  array  n 新建操作 new
 * @param  array  d 删除操作 delete
 * @param  number  i 需要转换元素的 index
 * @param  number  j 需要删除元素的 index
 * @param  string  b 比较字符串
 */
const compare = (r, n, d, i, j, b) => 
  const min = Math.min(r.length, n.length, d.length);

  switch (min) 
    case r.length:
      return [...r, patchObj(i, actionType.TYPE_REPLACE, b[i])];
    case n.length:
      return [...n, patchObj(i, actionType.TYPE_NEW, b[i])];
    case d.length:
      return [...d, patchObj(j, actionType.TYPE_DELETE)];

上面需要注意的是，我们一组保存了多个数组对象，不要对原数组进行操作，每一次操作我们都需要拷贝一个新的数组对象。

具体的的 diff 代码参考 diff 代码

得到了，patches 对象，剩下的我们就需要 patch 了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
 
const patch = (a, diffs) => 
  let aList = a.split(‘‘);
  let delCount = 0; // 删除之后，后续的index计算需要加上之前删除的数量
  diffs.forEach((diff) => 
    switch (diff.type) 
      case actionType.TYPE_DELETE:
        aList.splice(diff.index - delCount, 1);
        delCount++
        break;
      case actionType.TYPE_NEW:
        aList.splice(diff.index, 0, diff.item);
        break;
      case actionType.TYPE_REPLACE:
        aList.splice(diff.index, 1, diff.item);
        break;
      default:
        break;
    
  )

  // console.log(aList.join(‘‘))

  return aList.join(‘‘)

具体代码参考代码地址

参考资料

以上是关于Levenshtein distance 编辑距离算法的主要内容，如果未能解决你的问题，请参考以下文章

通俗解析莱文斯坦距离(Levenshtein Distance)计算原理(最小编辑距离)

C#实现Levenshtein distance最小编辑距离算法

Levenshtein Distance莱文斯坦距离算法来计算字符串的相似度

计算两组标签相似度算法——levenshtein distance 编辑距离算法

编辑距离算法详解：Levenshtein Distance算法

字符串相似度算法——Levenshtein Distance算法