归并排序算法思想

Posted 2022-03-08 yunrui-blogs

归并排序

###### 这次我们来讲述归并排序的基本思想。

• 归并排序，首先把一个数组中的元素，按照某一方法，先拆分了之后，按照一定的顺序各自排列，然后再归并到一起，使得归并后依然是有一定顺序的 。

• 归并排序算法可以利用递归的思想或者迭代的思想去实现。首先我们先把一个无序的数组去拆分，然后利用一定的规则，去合并。类似于二叉树的结构。其总的时间复杂度为O( n log n)。

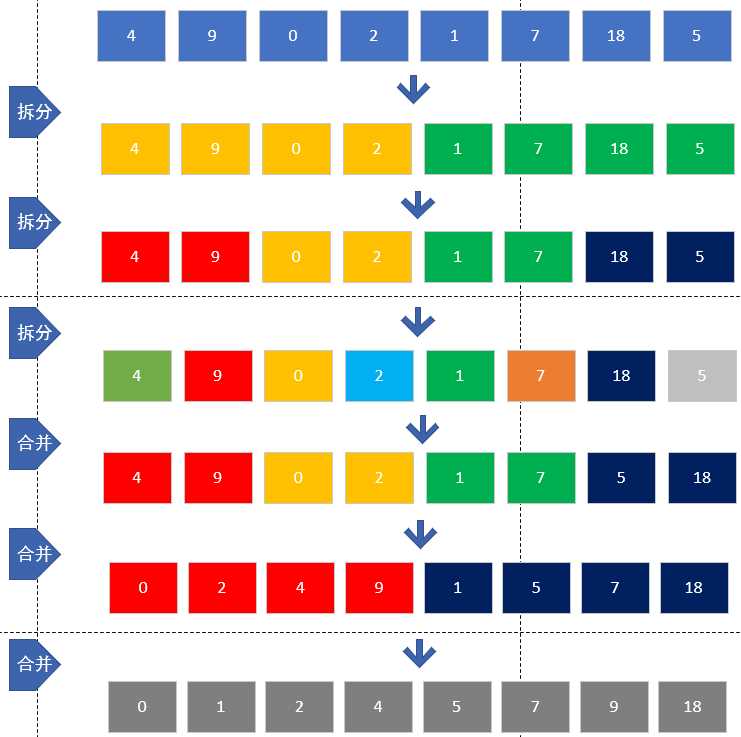
示例图如下:

• 首先我们看到，一个无序的数组如下，为了简约，以及简便解释，我们定义了8个元素。

• 然后，我们把该8个元素进行划分，分成左边四个，和右边四个，如下图。

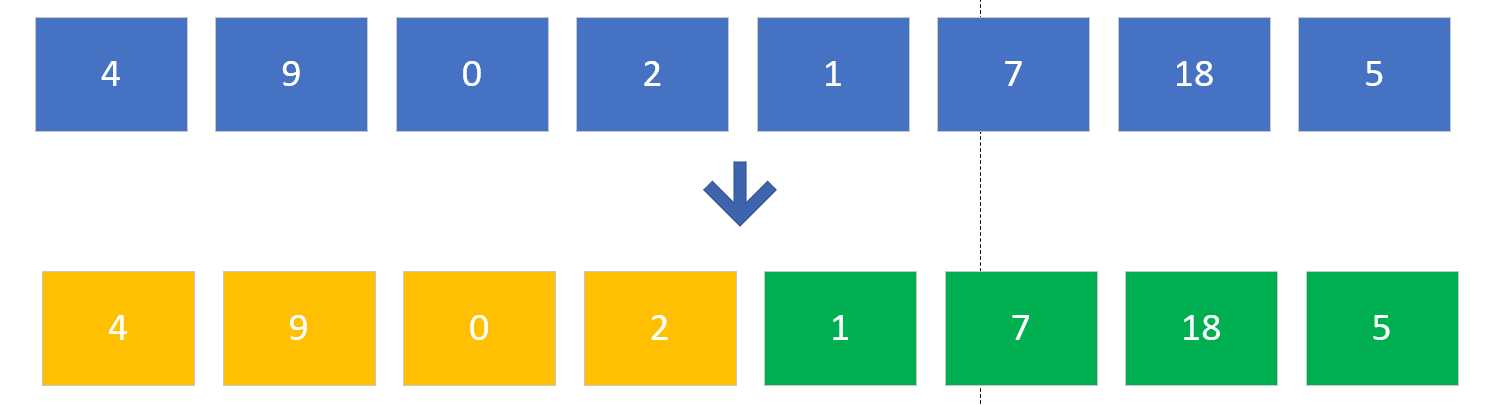
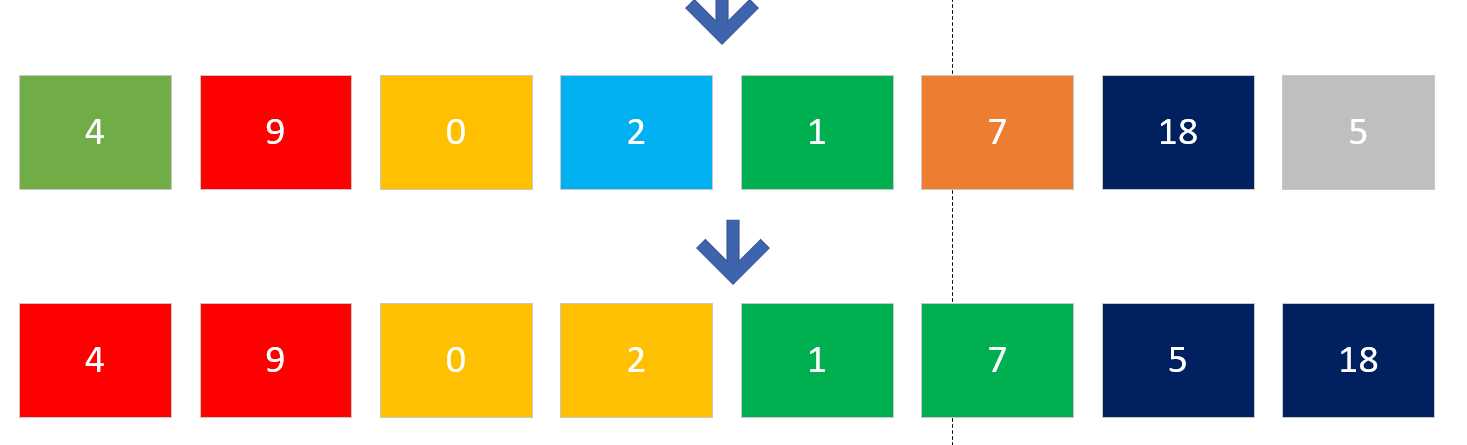
• 依次按照上边的方法，把剩余的数组继续拆分，一直拆到只剩下一个元素的时候，停止。如下图

[photo3][photo-3]

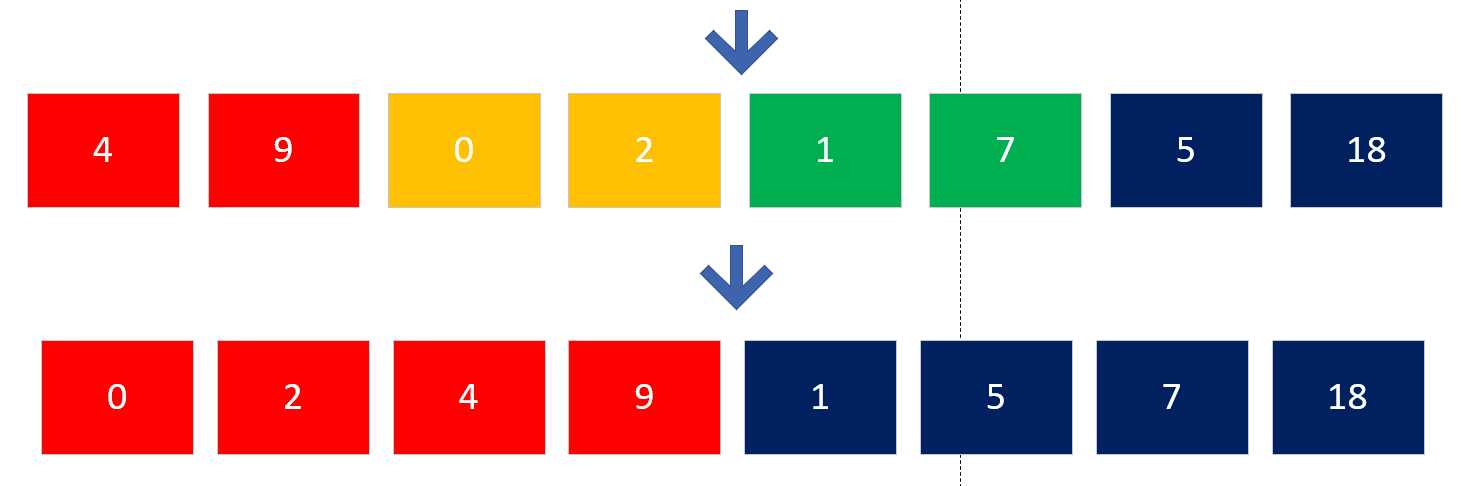
• 由于存在8个单独的子元素，然后我们两两把元素合并，并且按照一定顺序排序(此处用从小到大的顺序排序)。如下图:

[photo4][photo-4]:

• 此时，我们可以看到我们又得到了四个不同颜色的数组，并且在这个数组里边，也是按照一定的顺序排好序的。随后，继续利用这种方法，把剩余的继续合并，一直合并到所有数都在一个数组里边。此时便是完成了合并。如下图演示：

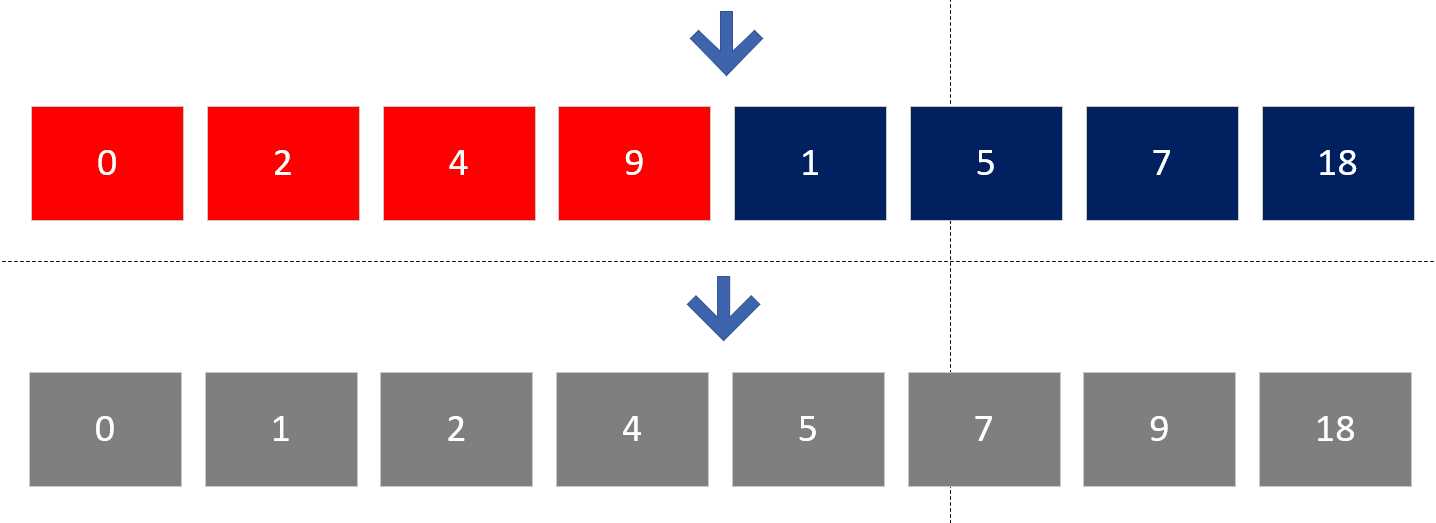
• 整个过程(包括拆分和合并)如下：

---

代码如下：

#include<iostream>
#include<cstdlib>
#include<vector>
using namespace std;

void Split(vector<int>& pos, vector<int>& temp, const int start, const int end);
void Merge(vector<int>& pos, vector<int>& temp, const int left, const int mid, const int right);
void MergeSort(vector<int>& pos, const int start, const int end);
void Display(vector<int>& pos);

int main()

    int n;
    cout << "请输入排序的数的个数" << endl;
    cin >> n;
    
    vector<int>pos(n, 0);//申请n个数
    
    cout << "请输入需要排序的数" << endl;
    for (int i = 0; i < n; i++)
        cin >> pos[i];//初始化数据
    
    Display(pos);//显示排序前的数组

    MergeSort(pos, 0, pos.size() - 1);//从第几个数开始，0个到最后一个数进行归并排序
    Display(pos);//显示排序后的数组
    
    pos.clear();
    return 0;


//拆分
void Split(vector<int>& pos, vector<int>& temp, const int start, const int end)

    if (start < end)//条件，不能分割为止
    
        int mid;//中间数定位
        mid = (start + end) / 2;
        Split(pos, temp, start, mid);//左边拆分
        Split(pos, temp, mid + 1, end);//右边拆分
        Merge(pos, temp, start, mid, end);//归并
    


//合并
void Merge(vector<int>& pos, vector<int>& temp, const int left, const int mid, const int right)

    int i, j, k;
    i = left;
    j = mid + 1;
    k = 0;
    /*
        i 表示第一个数组，从左到中间的数
        j 表示第二个数组，从中间到右边的数
        k 表示临时数组中的下表
    */
    while (i <= mid && j <= right)//两个数组判比
    
        if (pos[i] <= pos[j])//如果左边的大于右边的
        
            temp[k] = pos[i];//左边的放进临时数组中
            k++; i++;//继续跟下一个比较
        
        else
        
            temp[k] = pos[j];//如果右边的大于左边
            k++; j++;//同样放入临时数组中，继续跟下一个比较
        
    
    //当一方数组中有剩余的时候，把他放进临时数组中，然后等待归并
    while (i <= mid)
    
        temp[k] = pos[i];
        k++; i++;
    
    while (j <= right)
    
        temp[k] = pos[j];
        k++; j++;
    
    //把临时数组中的内容复制到实际数组中
    for (int i = 0; i < k; i++)
        pos[left + i] = temp[i];


//排序算法
void MergeSort(vector<int>& pos, const int start, const int end)

    vector<int>temp(pos.size(), 0);//创建临时数组
    Split(pos, temp, start, end);
    temp.clear();


void Display(vector<int>& pos)

    cout << "排序后的数组如下" << endl;
    for (int i = 0; i < pos.size(); i++)
    
        cout << pos[i] << " ";
    
    cout << endl;

---

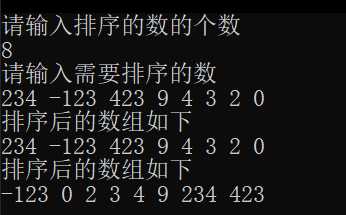
程序执行结果图

---